The Hammer-Aitoff Projection

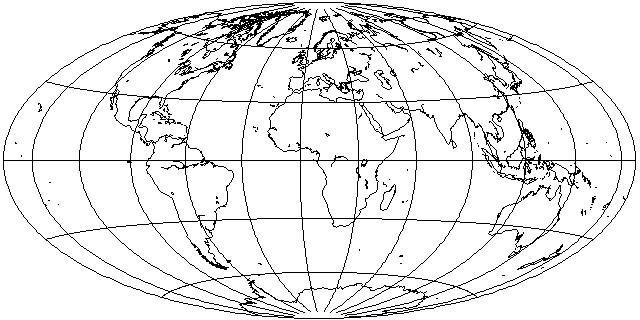
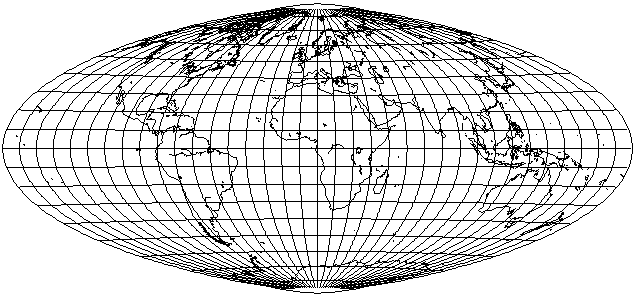
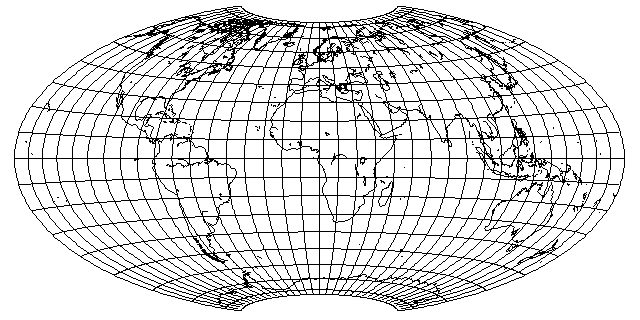
This map projection is an equal-area map projection which displays the world on an ellipse.

However, it is completely unlike the Mollweide projection. In the conventional case, the parallels are curved, and there is no stretching at the center of the map.

This map was created from a hemisphere of the equatorial case of Lambert's Azimuthal Equal-Area projection by two steps: first, divide the longitude of every location by two, to squeeze the whole world into a hemisphere, then compensate by stretching the circular map until it is twice as wide as it is high.

This is the Lambert Azimuthal Equal-Area projection:

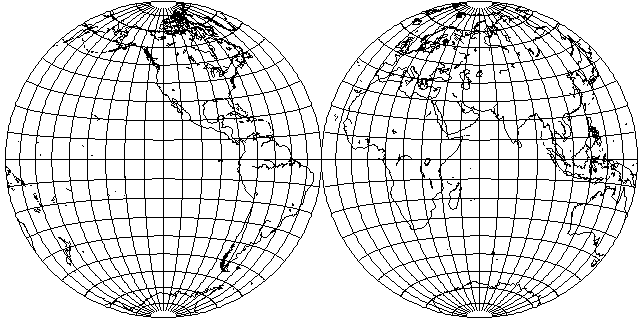
And here is what the world would look like in a single hemisphere of it, with longitude divided by two in order to squeeze it in.

Stretch that out to twice its width, and the vertical stretching from squeezing everything in is compensated for:

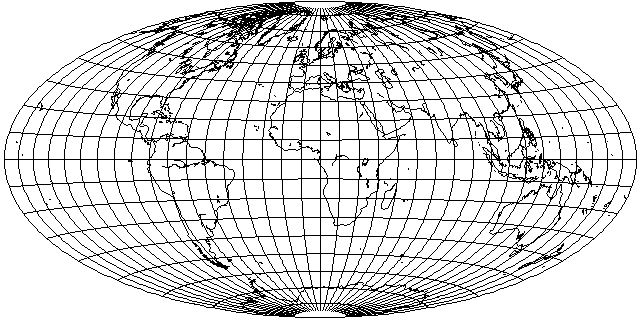
This trick is similar to the method by which the Miller Cylindrical projection was made from the Mercator projection, or by which the Lagrange projection was made from the Stereographic projection. Ernst Hammer (1858-1925) described this projection, directly inspired by the Aitoff projection which was based on the Azimuthal Equidistant, in 1892.

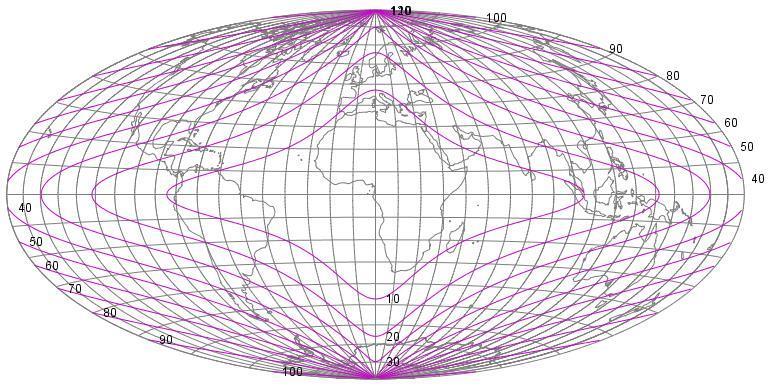
This is a chart, from Flex Projector, of the distribution of angular distortion in this projection:

This projection is also popular in the oblique case, producing maps like this:

The map above is in Bartholomew's Nordic Projection, where the globe is tilted forwards by 45 degrees along the prime meridian.

One source claims that the Nordic, Atlantis, and Regional projections made their appearance in a new 1950 atlas. I've also seen 1951 as the date. However, still another gives the date of 1948 for at least one of these novel projections from Bartholomew; I am inclined to accept the earliest of these dates, as I have seen positive evidence of the existence of a 1948 edition of the atlas concerned.

As we saw in the page on the Mollweide projection, though, Bartholomew's Atlantis projection was partly anticipated by a Transverse Mollweide from 1912 by Colonel Sir Charles Close, who also developed an oblique Mollweide, so, if anything, it's surprising that Bartholomew's Nordic projection was not anticipated even earlier (and perhaps it was, but I haven't been able to find an example yet).

Instead, the earliest example that I have been able to find so far of a Hammer-Aitoff in an unconventional aspect is the one that appeared in Athelstan Spilhaus' paper, Maps of the Whole World Ocean, which appeared in the July 1942 issue of the Geographical Review. This is in the same orientation as the map on August's conformal projection, which, as I've noted, may be the only place many people have seen that projection.

Here is what Dr. Spilhaus' map on the Hammer-Aitoff projection looked like:

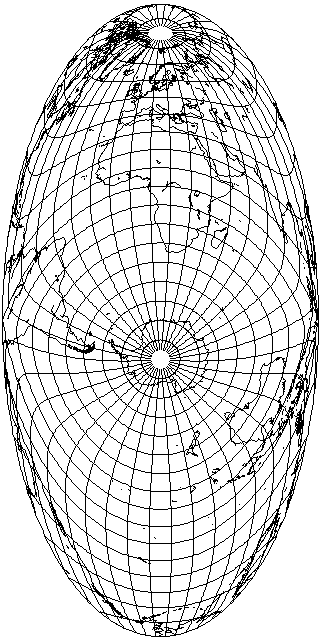
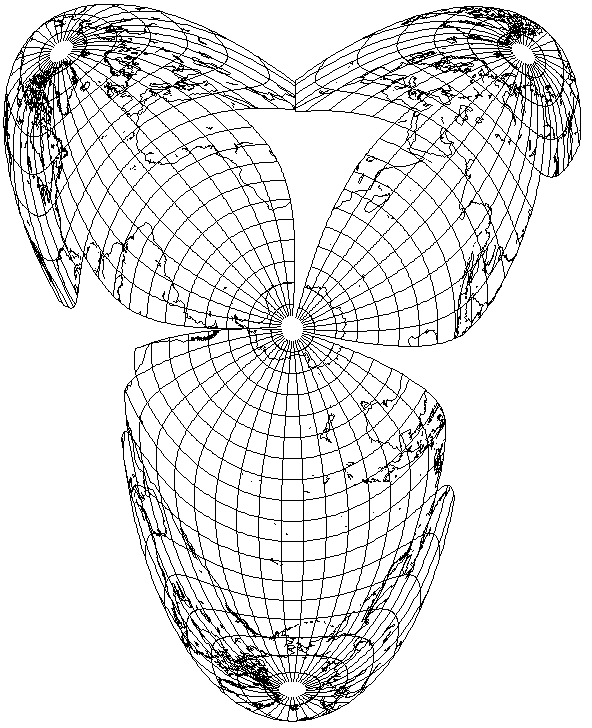
Many years later, he used three Hammer-Aitoff projections, one for each of the Pacific, Atlantic, and Indian oceans, combining the three lobes to make a map of the World Ocean. I illustrate here the three component projections, without attempting to stretch the map to fit them together as he did:

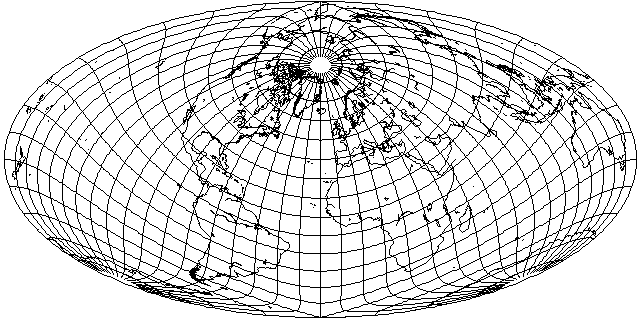
Another very popular projection of this type also tilts the globe forwards by 45 degrees, but along the meridian of 10 degrees East longitude; and as well, the projection, instead of being stretched from a circle to an ellipse with a 2:1 aspect ratio, is only stretched to a 7:4 or 1.75:1 aspect ratio:

This is Briesemeister's projection, which dates from 1953. In the 1970s, it was even used in a few Hammond atlases.

Trying to do better with this kind of projection, I attempted:

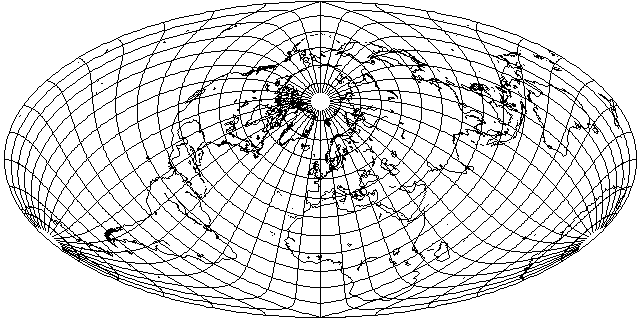
Here, the globe is only tilted forwards by 40 degrees, and along the meridian of 20 degrees West. This avoids cutting New Zealand in half, although now it's separated from Australia.

If the focus is on North America and Europe, North America is now significantly less distorted. But the bad news is that Japan, already badly stretched in the Briesemeister projection, and even more so in the Nordic projection, is now stretched much more, enough to make this projection almost useless for it, as well as for Korea and even the Philippines.

So if that didn't work out, let's try changing the projection in the opposite direction:

Here, the globe is tilted forwards by 50 degrees, along the meridian of 30 degrees East longitude.

South America seems to be less distorted. Europe is still central, North America is somewhat worse off. But now Japan, Korea, the Phillipines, New Guinea, and so on fare much better. Hawai'i, however, is now right at the edge of the map.

This suggests one last attempt to improve things:

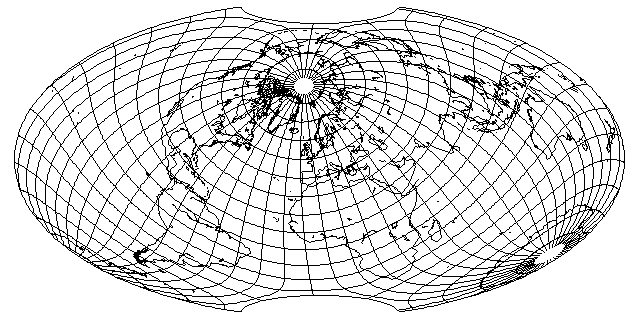
Here, the globe is tilted along the Prime Meridian, but by 60 degrees. North America is now much less distorted, and Japan, Korea, and the Phillipines are also better off as well. Instead, the price is paid of greater distortion for South America and Africa, so this aspect more strongly favors the economically developed nations.

Earlier, in the page on the Mollweide projection, Bartholemew's Atlantis projection was shown. This aspect made use of the fact that the Mollweide projection stretches areas near the Equator to put North America and Europe in the least-distorted areas of the projection. Thus, this projection would not work as well with the Hammer-Aitoff projection. However, the same result can be obtained by stretching the Hammer-Aitoff projection vertically, as the Briesemeister projection demonstrates.

Instead of placing the North Pole at 45 degrees West on the map, I place it at 30 degrees, so as not to cut New Zealand in half, and I stretch the projection more than Briesemeister did, so that the aspect ratio is 8:5, and here is my result:

Of course, a fully generalized oblique projection is also possible. On these pages, I've noted that both the Modified Gall projection, and the Oxford projection, used in several Oxford atlases, were designed by Brigadier Guy Bomford. As well, they also used this aspect of the Hammer-Aitoff projection, and this time, it being called the Bomford projection, his connection to it was not obscured:

It was also used in an Oxford atlas, from 1951, although it does not appear to have become a fixture of Oxford atlases as the other two projections of his had for some time.

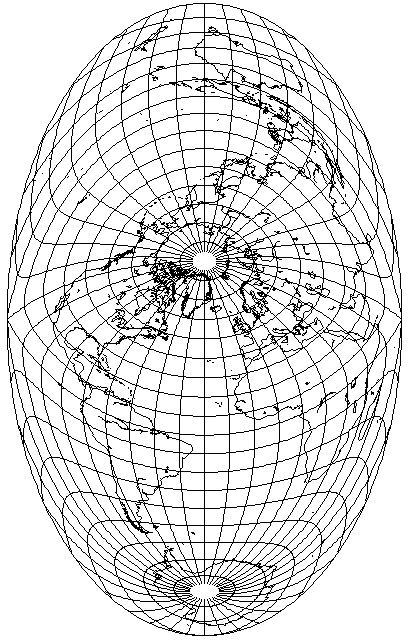
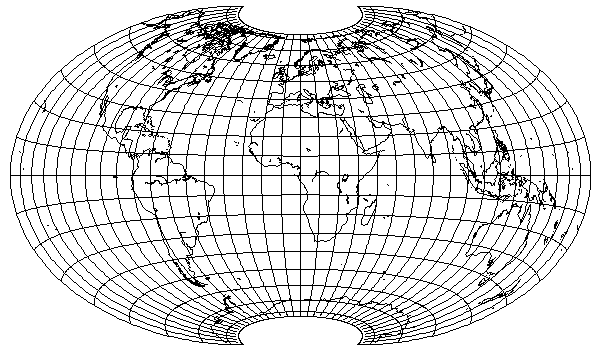
And then there is the more extreme aspect, less successful at reducing distortion for the major continental areas, which I use frequently on these pages, that has the dubious advantage of avoiding the need to split Antarctica in two. Its most noticeable flaw, perhaps, is that it imposes excessive distortion on Africa in most projections:

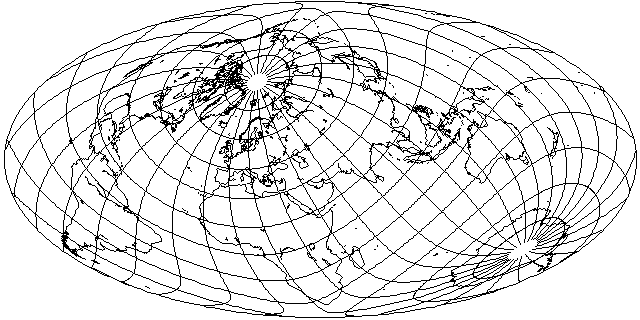
Compare the Mollweide projection in precisely the same orientation:

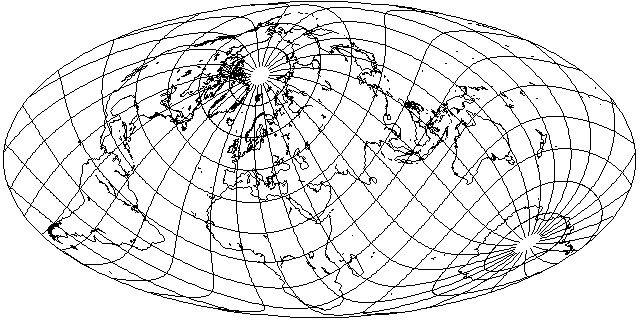
Inspired by the Bomford projection, I tried to see if I could take my oblique aspect, and still keep Antarctica uninterrupted, and reduce the distortion:

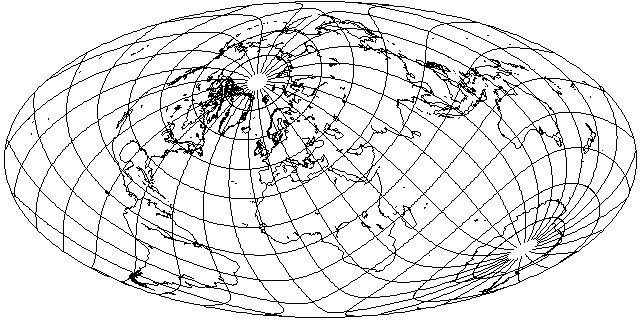
And, indeed, it's easy enough to move Africa out of harm's way, but South America continues to be stretched horizontally a great deal. Since, in fact, South America is now worse off, perhaps if the map is rotated less, a better compromise between those two continents might be achieved:

And by substituting a small rotation for a large one, South America is not made worse by as much, and Africa is already much improved, so this is a better compromise.

Also, since most of the areas on the map where distortion is an issue seem to be stretched horizontally,

above the vertical stretch used in Briesemeister's projection is tried to see what benefit it may bring.

The basic idea behind the Hammer-Aitoff projection is simple enough: first, place the whole world in one hemisphere by the simple expedient of dividing all longitudes by two, then to compensate for that, stretch the map out twice as wide.

Instead of using a factor of two, a factor of four was used to create the Eckert-Greifendorff projection:

Note that Adams' Equal-Area projection, which spaces the parallels as they are spaced on the central meridian of an equatorial Lambert's Azimuthal projection, could be thought of as the limiting case of this kind of manipulation, as the factor approaches infinity.

Recently, Tobias Jung tried the idea of changing the factor in the other direction; to obtain this projection,

it has to be lowered all the way to 1.2 or 6/5.

If one instead only lowers the factor to 1.5

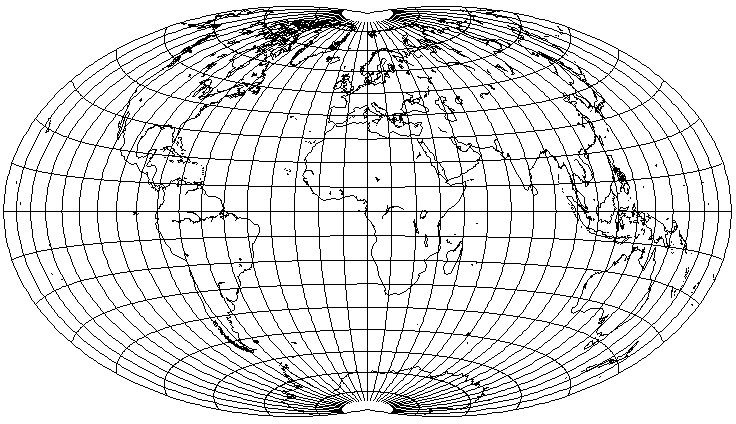
the result may not look too impressive; one might ask, why bother not just using the standard Hammer-Aitoff projection? However, this resulting projection somewhat resembles an optimal equal-area projection recently devised by Daniel Strebe, but that projection has a more pronounced indentation at the poles. One benefit of having a shape like this is that shear is reduced in the corners of the map area; thus, North America is less distorted in the map shown here.

If one instead changes the stretch factor to 1.3333... or 1 1/3, one obtains the following

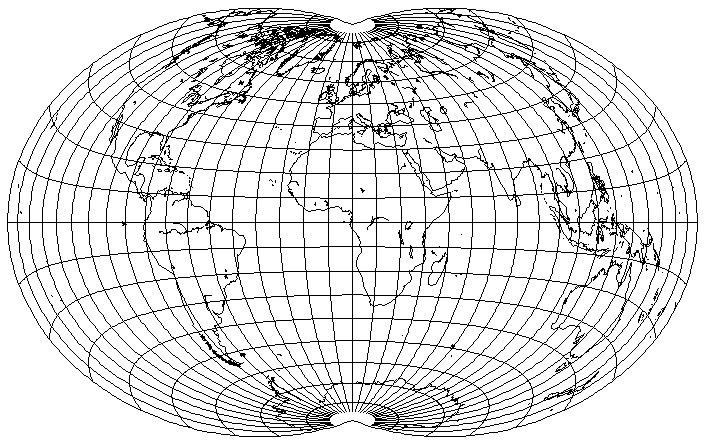
with an even closer resemblance to the projection devised by him, at least in the degree of indentation of the poles. However, the vertical stretching at the Equator is much greater than in his optimized projection, and it's also taller, in proportion to its width than that projection.

Since it looks so nice, what would happen if the orientation used by Bartholomew for his Nordic projection were used with it?

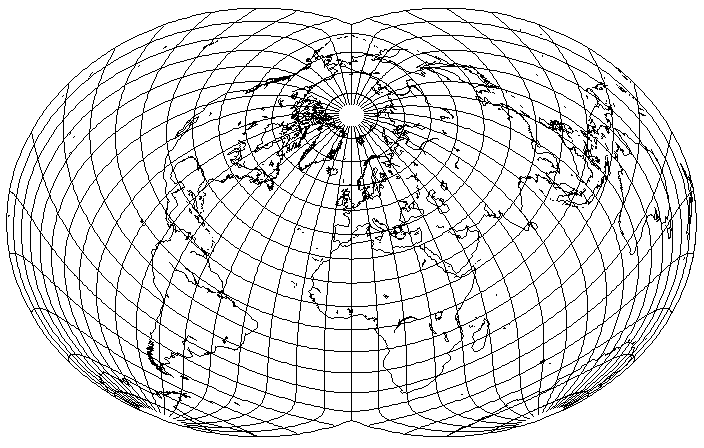
This looks very good for most of the world; however, Australia and New Zealand are in an area of the map with high angular distortion. A slight rotation will help with this:

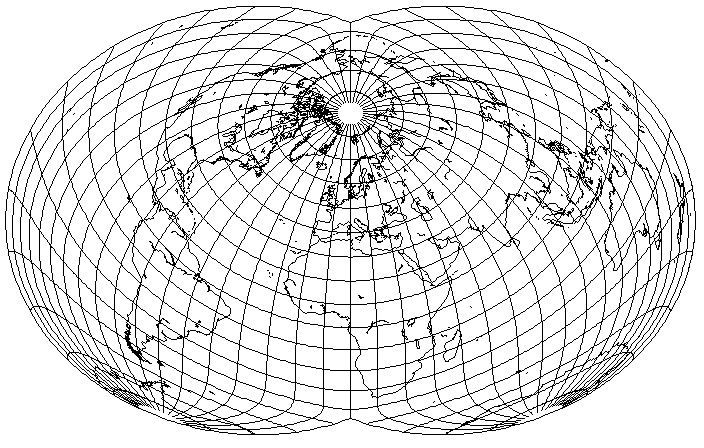
A larger rotation would help Australia even more,

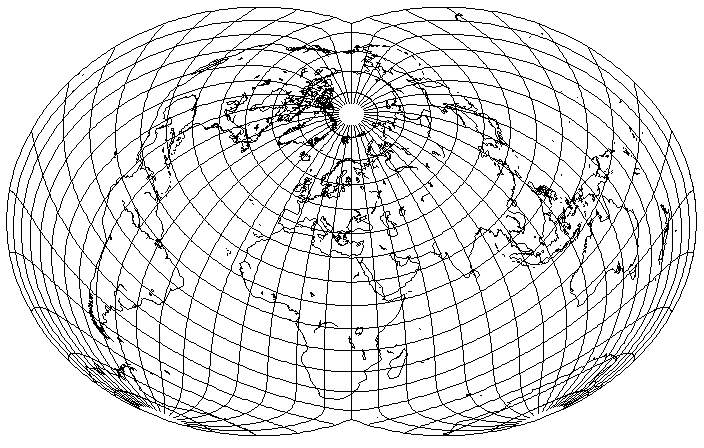
at the cost of more distortion for North America.

Given that the version with a stretch factor of 1.5 has less stretch at the Equator at the edges, it might be kinder to Australia if used in the same aspect as the Nordic projection:

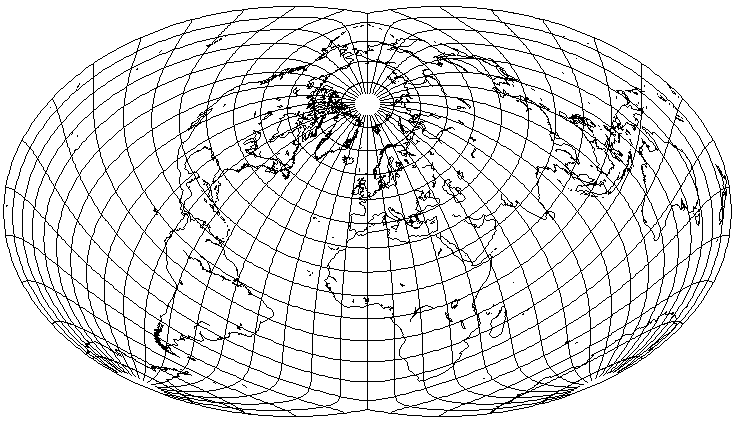
And indeed, Australia does look better, so if it was desired to improve its appearance,

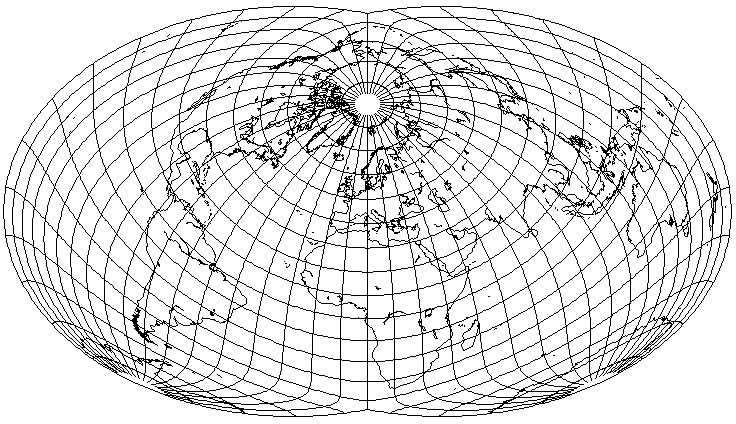
only a small rotation would be needed.

This projection was devised by Hammer, using the idea first used by Aitoff in making a compromise projection in such an ellipse from the Azimuthal Equidistant projection. Aitoff, however, then returned the compliment by using the basic method behind the Lagrange Conformal projection, but this time superimposing one equal-area cylindrical projection upon another. The ratio in scales was 9 to 10, and this time a compensating stretch was needed, to create an equal-area projection which I find quite appealing:

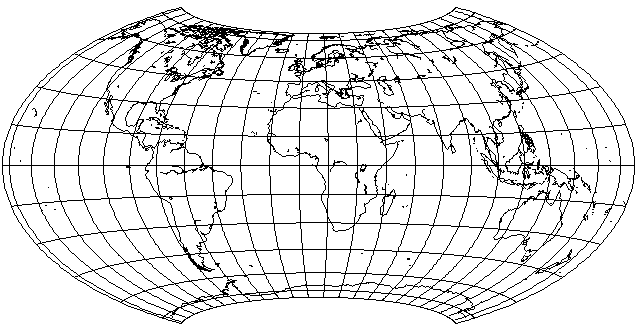
Since the same transformations that can be applied to the Hammer projection can also be applied to the Adams projection, one could further reduce shear by interrupting the modified Adams projection, and combining it with the Aitoff equal-area projection, somewhat after the manner used in the Oxford projection, to form a result like the following:

However, to make the pole lines shorter, to try to make the result a more balanced compromise between the Hammer-Aitoff on the one hand, and the cylindrical equal-area on the other, I used the sine of 75 degrees, or .9659258, as the factor to produce this projection:

However, that didn't seem to be an improvement, since the extra shearing seems to be worse than the stretching in the previous projection. However, in an oblique case of the projection:

it's possible to move all the important land masses out of the areas with high shearing, producing quite a pleasing result.

Noting that Tobias Jung had to reduce the stretch down from 2 all the way to 1.2 in order to get a pleasingly apple-shaped projection, I wondered if a lesser reduction, to a stretch of 1.5, would work with short pole lines; again, I used the sine of 75 degrees as the compression factor:

Also, if we reduce stretching at the cost of more shearing, we can then reduce shearing through the kind of interruptions tried above with Aitoff's projection, to which a projection such as the above, with a shorter pole line, might be more suited.

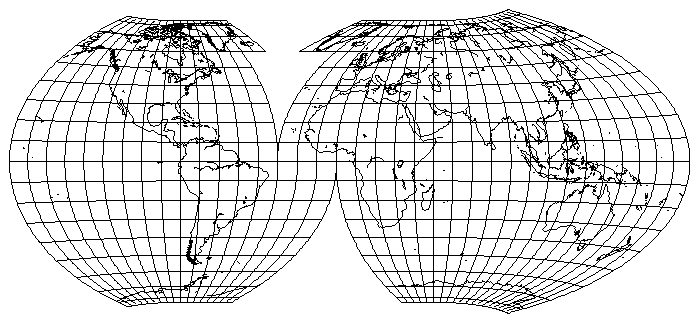
A projection of this type which is found as a world map on some atlases is the Wagner VII projection, also known as the Hammer-Wagner projection. The factor it uses is the sine of 65 degrees, or 0.906307787, for the superimposition of equal-area cylindrical projections. Simply using this factor (with, of course, inverse stretching of the map to keep the center of the map conformal) will produce the following map:

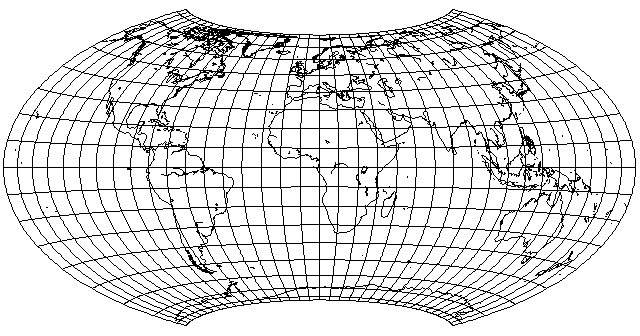
But the actual Hammer-Wagner projection, instead of being derived from an equal-area latitude transformation applied directly to Hammer's projection, moderates the compression of longitudes away from the prime meridian; instead of compressing the 360 degrees of longitude of the sphere into a hemisphere of Lambert's Azimuthal Equal-Area, with 180 degrees of longitude, it compresses the sphere further, into only 120 degrees of longitude, and then expanding it back, leading to a result like this:

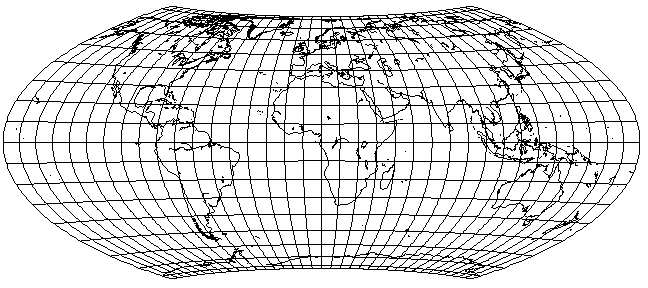
But even that isn't quite the actual Wagner 7 or Hammer-Wagner projection. The projection is then stretched vertically, so that there are two conformal points on the prime meridian, located in temperate latitudes. I had some difficulty in calculating the factor of stretching, exclusive of that which compensates for the latitude and longitude transformations, which my mapping program is designed to automatically provide, that this projection uses, but I now believe it to be a factor of about 1.2650925, yielding this projection:

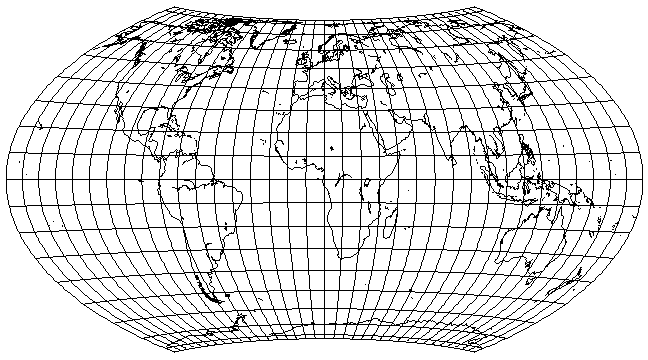
This equal-area projection has become quite popular for world maps in a number of recent atlases.

Thanks to G.Projector, I no longer need to guess,

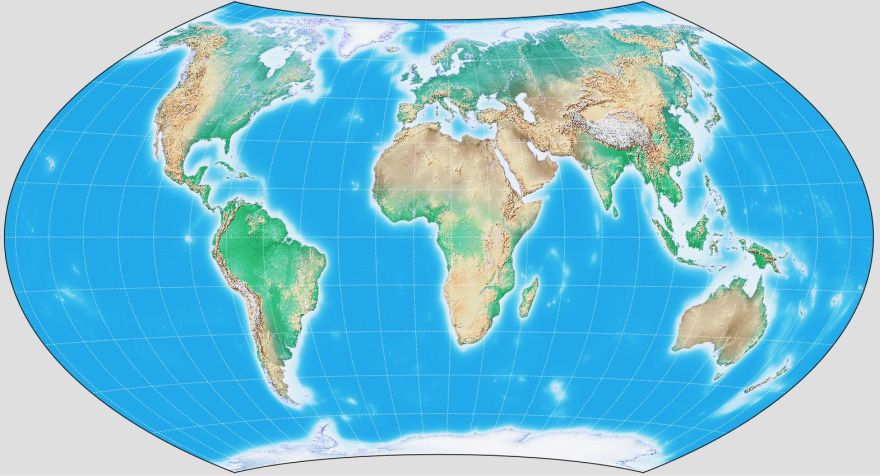
but can provide an image which I know is what the projection really looks like.

And thanks to Flex Projector,

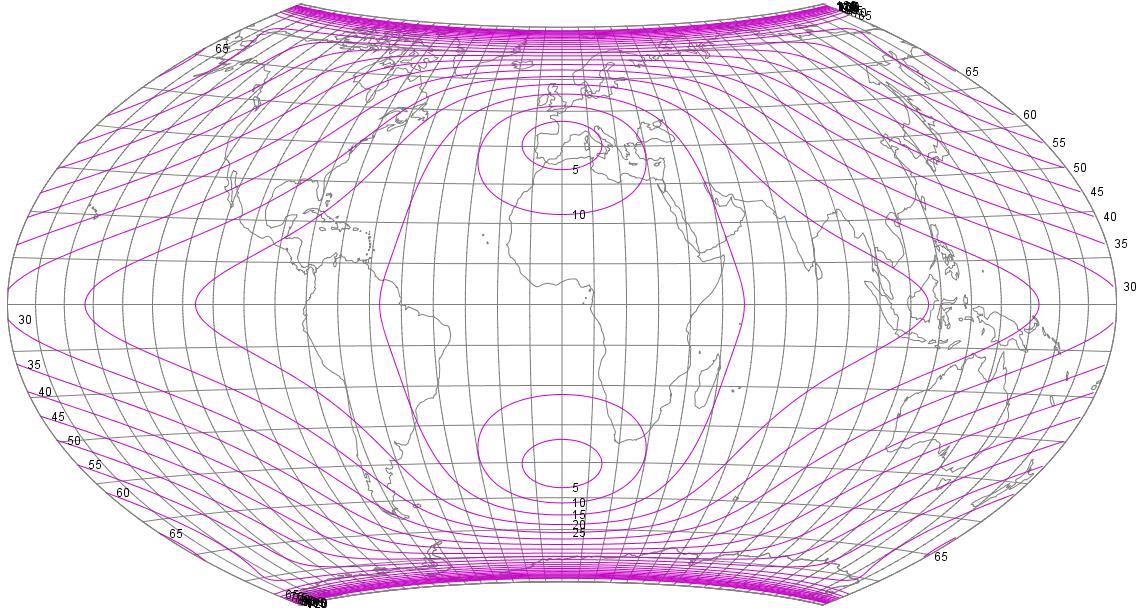
here is a diagram of how angular error is distributed on this attractive equal-area projection. Of course, due to it having pole lines, error increases very rapidly near those lines.

A paper by D. R. Steinwand, J. A. Hutchinson, and J. P. Snyder, in which an extensive analysis of shape distortion in equal-area projections was described, recommended four equal-area projections for use in statistical maps: the Goode Homolosine projection, the interrupted Mollweide, this projection, and the pseudocylindrical Wagner IV projection.

In the section on the Lagrange Conformal projection, I note that both that projection and the Hammer-Aitoff projection featured here provide a distribution of error that is perhaps very well suited to a number of countries which neither lack a long axis (like France) nor favor one to an extreme extent (like Chile), and, thus, are not best served by either an azimuthal projection on the one hand, or a cylindrical, conic, or polyconic projection on the other.

Here, then

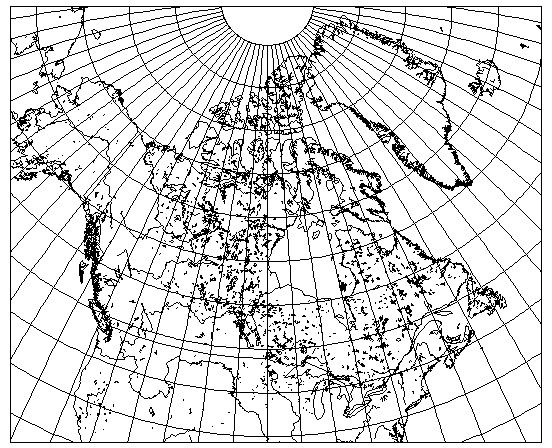
is a map of Canada, drawn in the central part of an oblique Hammer-Aitoff projection centered on 55 degrees North latitude and 95 degrees West longitude.

For another example of how an oblique Hammer-Aitoff projection might be used for an area elongated in extent, here is a map of the Atlantic Ocean on such a projection:

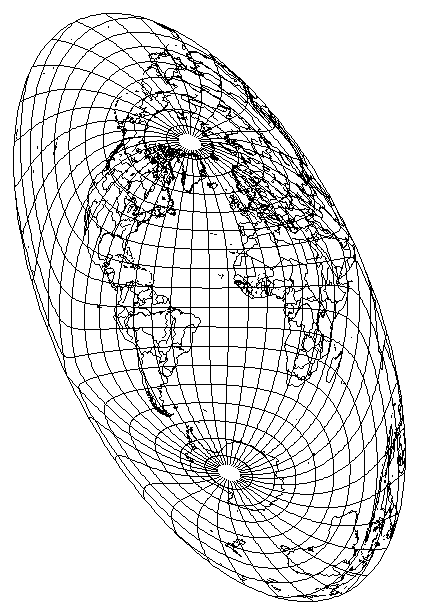
A very interesting variation on this type of projection was recently devised by Rolf Böhm.

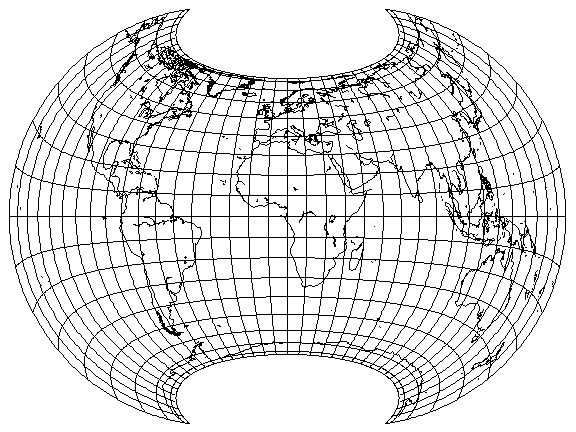
Here, the pole line is taken from the parallel of 60 degrees latitude on the Lambert Azimuthal Equal-Area, so the sine of 60 degrees is used for compressing the latitude by means of cylindrical equal-area projections.

The 360 degrees of longitude, instead of being compressed into the 180 degrees of a hemisphere, as on the Hammer-Aitoff, are compressed into 264 degrees of longitude.

And there is a slight vertical stretch, about 6.9%, so that the central meridian is exactly half as high as the Equator is wide.

This projection has the interesting and useful characteristic that the boundaries of certain regions within it of maximum angular area are almost rectangular in shape. This lends itself to using the projection for an attractive map of Eurasia, as its inventor demonstrated:

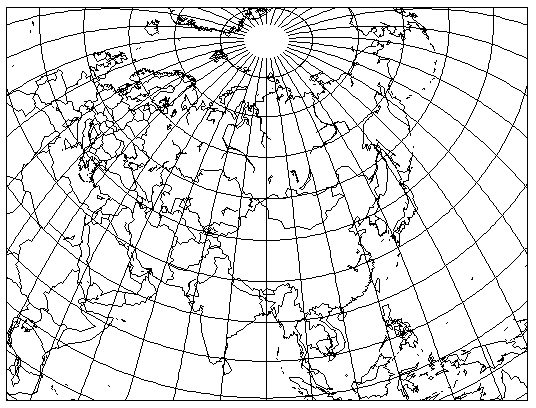
The flexibility in the parameters that were used to create the Wagner VII projection can be employed in other ways.

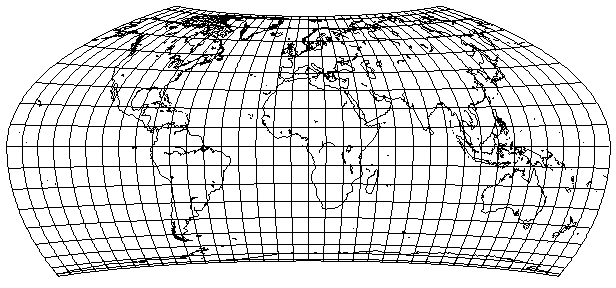
The projection above follows the scheme of the Wagner VII projection, but with different parameters; of the three parameters, one of them is different for the Northern hemisphere and the Southern hemisphere; the other two are the same, so the two projections will join smoothly at the equator.

Like the Wagner VII projection, longitude is divided by three before using the equatorial case of the Lambert Azimuthal Equal-Area projection.

There is a final vertical stretch by a factor of 1.08, significantly milder than that which is used in the Wagner VII projection.

In the Northern Hemisphere, a slightly shorter pole-line is obtained than in the Wagner VII: the world is mapped to a cylindrical equal area projection that is shrunk to 92% of its size, and then that transformation is reversed. In the Southern hemisphere, on the other hand, because the land areas there don't extend as far south as those in the Northern hemisphere extend north, to make the projection more like a cylindrical equal-area projection, the first projection is shrunk to 60% of its size.

This was inspired by the Strebe Asymmetric projection, but instead of using the more complicated transformations that it does, it remains a bit more straightforward by sticking to the toolkit used for the Wagner VII projection.

Applying asymmetry to the projection above with short pole lines and a stretch factor of 1.5, using the sine of 75 degrees for the Northern hemisphere, but the sine of 40 degrees, approximately 0.6427876, for the Southern hemisphere, I get:

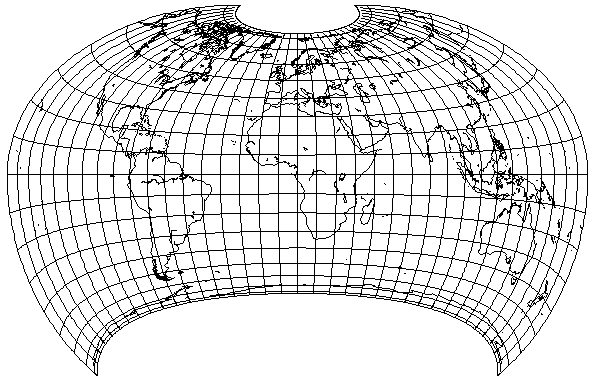
The pointed corners at the bottom are a problem, but of course one could just trim off the bottom of the map with a straight line to hide them.

Another thing suggested by this projection is: projections like the Sinusoidal and the Mollweide lend themselves to being used in an interrupted form because they have an Equator of constant scale. But this Equator of constant scale has a cost in higher distortion elsewhere in the projection. Is the small are on the Equator where the Eastern and Western hemispheres are joined on a typical interrupted projection really all that useful?

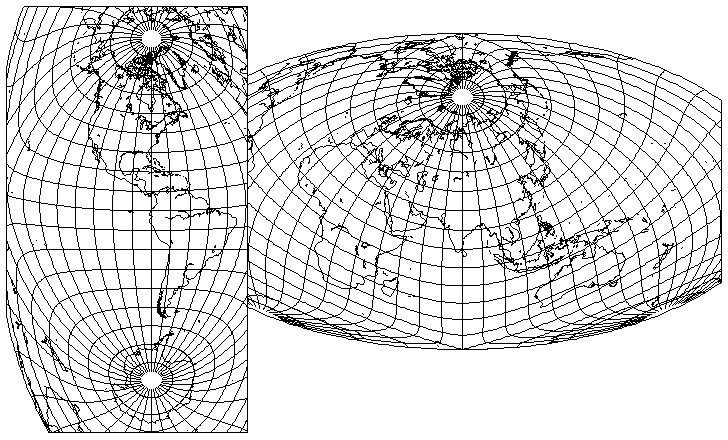
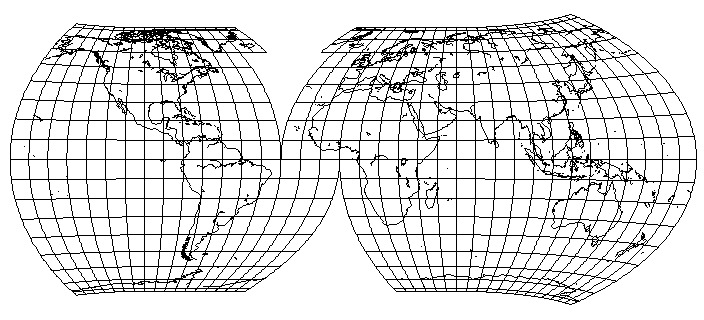
So, as the Hammer-Aitoff projection is able to attractively cover a large area, why not improve on the distortion it has when used for the whole world by using two projections, with the lands of the Western Hemisphere centered in one, and those of the Eastern Hemisphere centered in the other?

The example above is very nice to Antarctica, and to Asia, but it is unkind to Australia. Still, it presents much of the world quite attractively.