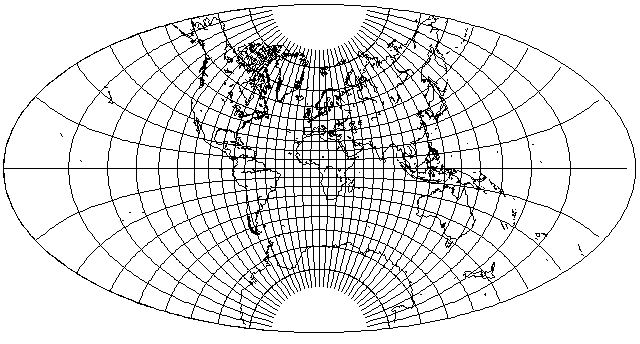
The popular Hammer-Aitoff projection is based on an idea by David Aitoff (1854-1933) which he originally applied to the equatorial case of the azimuthal equidistant projection, in 1889, yielding this:

rather than to the equatorial case of Lambert's azimuthal equal-area projection, as was suggested later, in 1892, by Ernst Hammer.
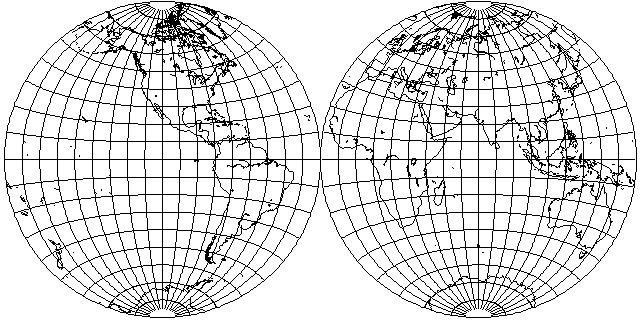
The Azimuthal Equidistant projection is not often used for conventional hemispheres, but if it was, it would look like this:
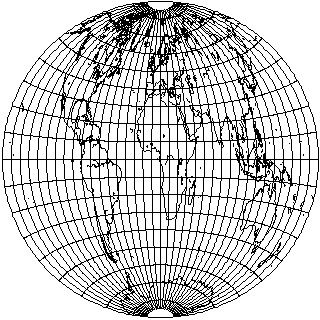
If one were to squeeze the whole world into one hemisphere by dividing the longitude in half, the result looks like this:
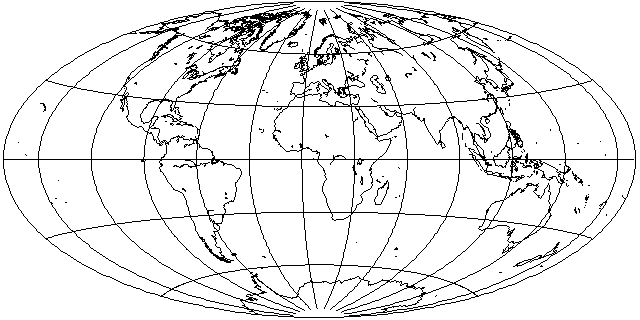
and then expanding it back by a factor of two yields the Aitoff projection:
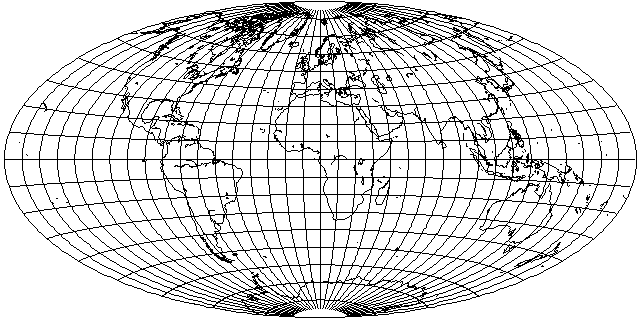
The Winkel Tripel projection, which is a popular projection in many European atlases,
is the arithmetic mean of it and a Plate Carrée projection with 40 degrees latitude as its standard parallels.
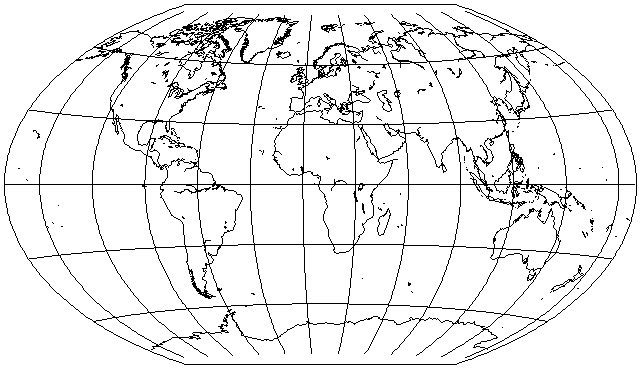
Actually, this is merely Bartholomew's variant of the Winkel Tripel projection, I have since learned; the arccosine of two over pi, which is about 50.459776 degrees, was the standard parallel used in Winkel's original Tripel projection, as illustrated below:
For the original Winkel Tripel projection, thanks to Flex Projector, here is the distribution of its angular error:
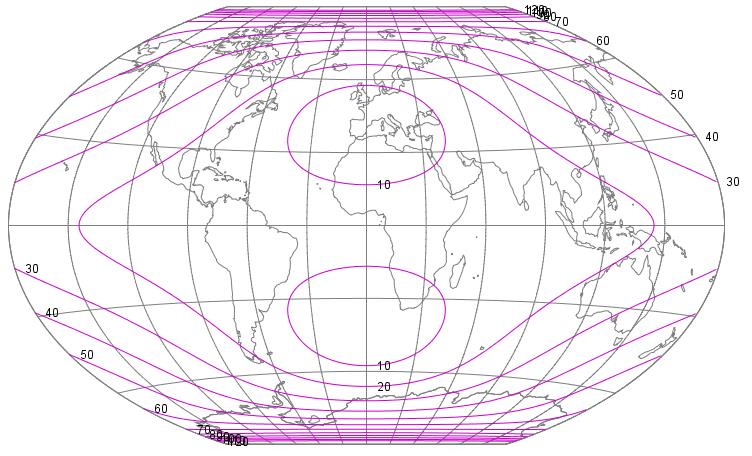
and of its error in area:
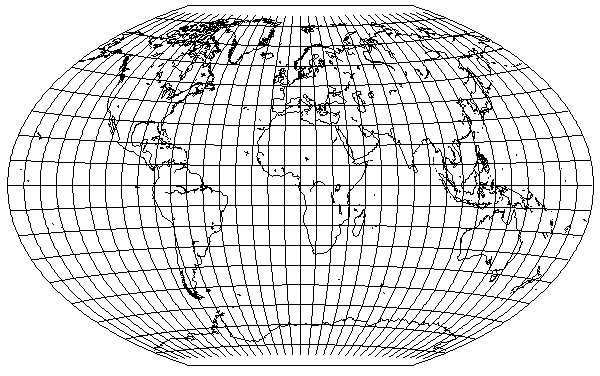
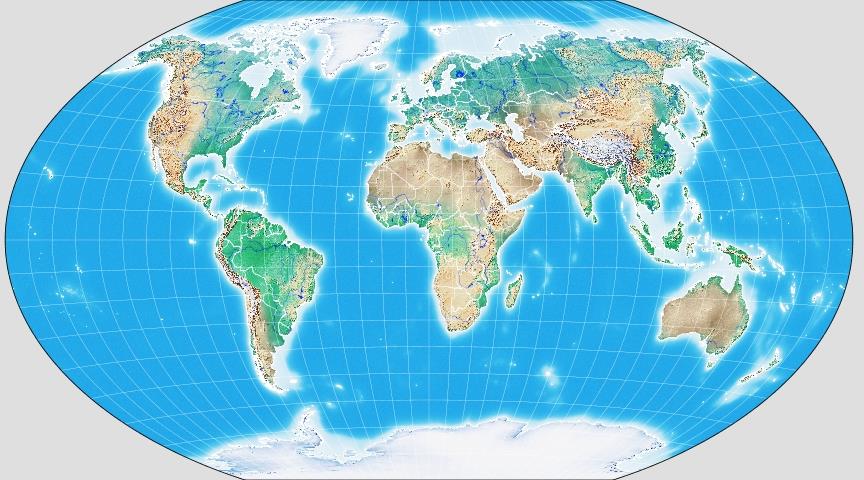
Here, thanks to G.Projector, is a pictorial version of the popular Bartholomew variant of the Winkel Tripel projection:
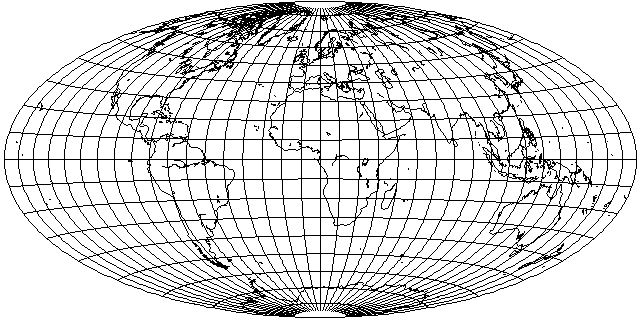
Comparing the appearance of the Hammer, or Hammer-Aitoff projection, based on the Lambert Azimuthal Equal-Area projection:
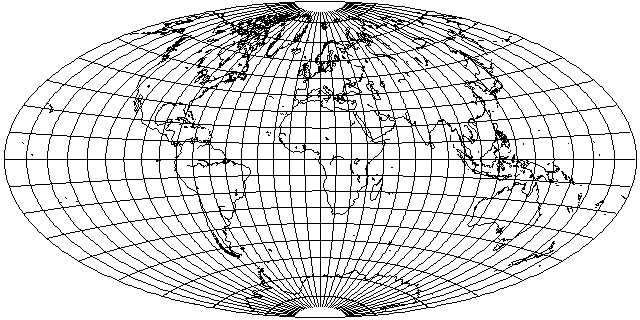
with that of the Aitoff projection, based on the Azimuthal Equidistant instead,

perhaps if one instead used a hemisphere of the Nell Globular, which can be thought of as resembling an average between the Stereographic and the Azimuthal Equidistant, and applied the Aitoff doubling of the meridians,
one would get a projection which was even more attractive in appearance, although at the cost of having more exaggeration of areas near the edge.
There is a completely different projection known as the Nell-Hammer, so calling this projection the Nell-Aitoff might be confusing.
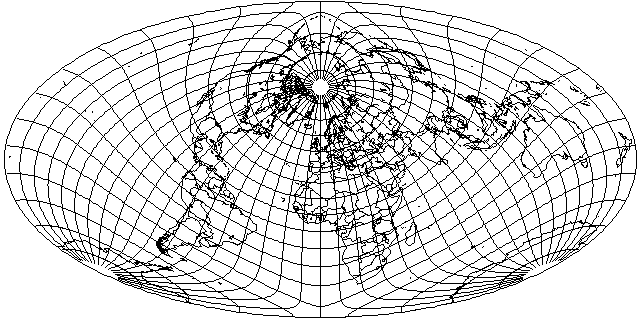
And it even turns out well in an oblique aspect, too!
Of course, one could also use the Stereographic itself, instead of Nell's Globular, as the starting point:
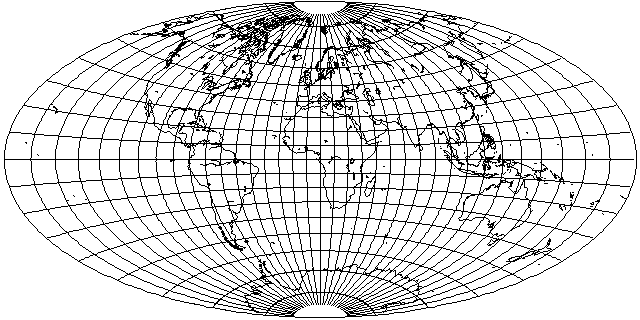
and this too produces an attractive projection, while not exaggerating scale quite as much as Adams' conformal projection of the world on an ellipse: