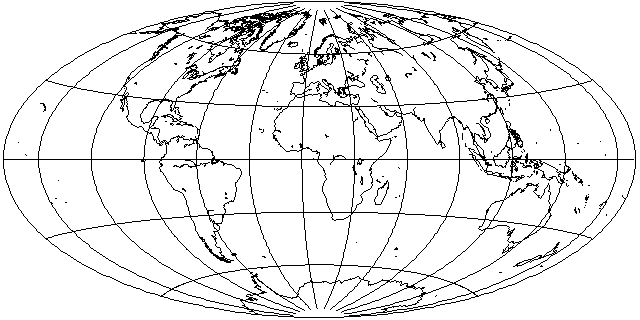
The popular Hammer-Aitoff projection is based on an idea by Aitoff which he originally applied to the equatorial case of the azimuthal equidistant projection, yielding this:

rather than to the equatorial case of Lambert's azimuthal equal-area projection.
Using a technique similar to that used to derive Aitoff's Equal-Area projection from the Hammer-Aitoff, but this time scaling the latitude, as well as the longitude, linearly, and using a scale factor of 0.8, one obtains the following attractive compromise projection:
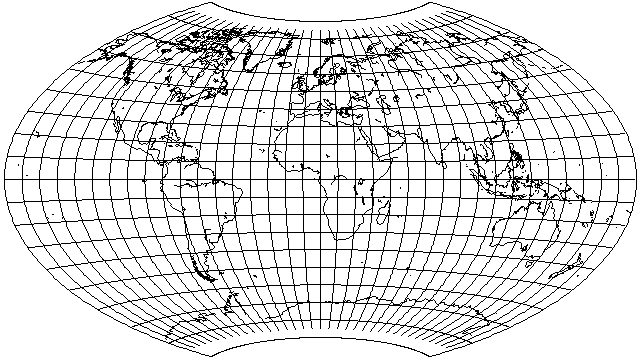
Here, we scale the latitude linearly, rather than by placing one cylindrical equal-area projection on top of another one, so a scale factor does not need to be very close to 1 in order to obtain a short pole-line.
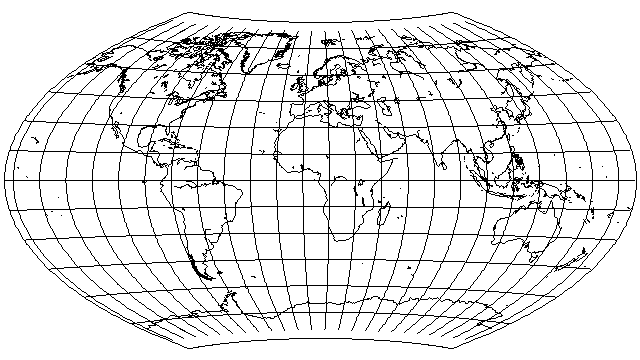
The Aitoff-Wagner projection, also known as the Wagner IX projection, is based on a similar principle; however, the latitude and longitude are not scaled by the same factor before being subjected to the Aitoff projection. Instead, the latitude is reduced to 7/9ths of its value, but the longitude is reduced to 5/9ths of its value, and then the Aitoff projection is performed (or, alternatively, the longitude is reduced to 5/18ths of its value, and then the equatorial case of the Azimuthal Equidistant is performed) and then the inverse scale factors are applied to the x and y values of the result. Here is the result, the Aitoff-Wagner projection:
Out of sheer perversity, here is what the arithmetic mean of the simpler projection I described before presenting the actual Aitoff-Wagner projection, with a scale factor of 0.8 in both directions, and the Van der Grinten(!) projection, looks like:
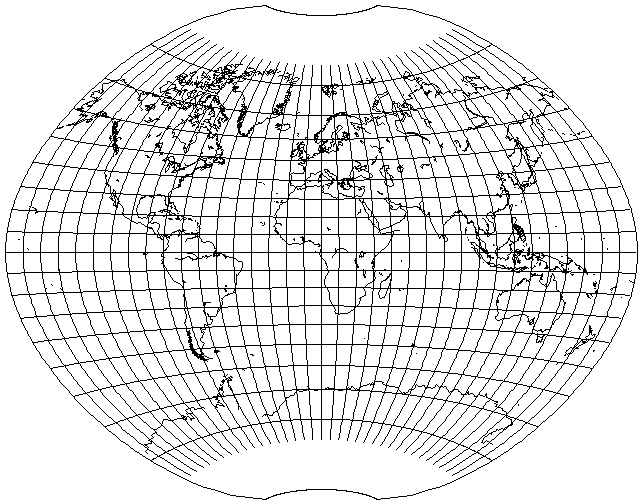
The projection above could be called the Projection Involving a Really Excessive Amount of Computation for a Projection with No Particular Properties, or PIREACPNPP for short. However, there's nothing wrong with playing with such a thing, as even if it is not suitable for practical use directly, if it looks attractive, one could approximate its appearance with a projection that is simpler to calculate.
However, there is a real map projection the appearance of which is somewhat in the same ballpark as this one, the Larrivée projection,
the formula for which is:
1 1
x = ( - + - sqrt( cos(lat) ) ) * long
2 2
lat
y = ------------------------------
1 1
cos( - lat ) * cos( - long )
2 6
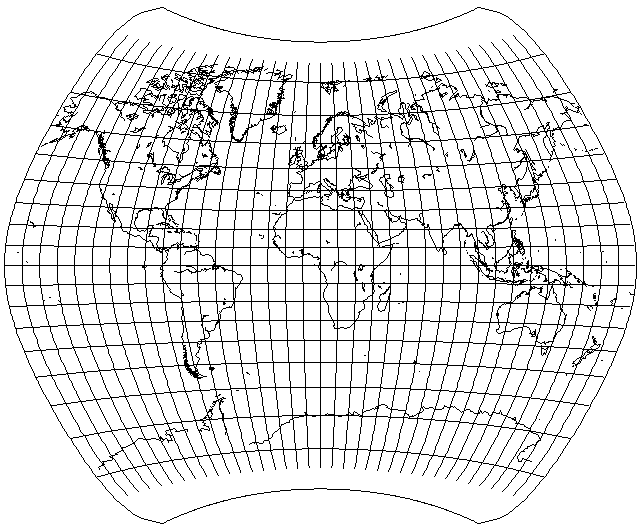
Although this is an interesting and attractive projection in its own right, and a reasonable alternative to the Winkel Tripel or the Van der Grinten for world maps in atlases, depending on the extent to which one wishes to move away from the Mercator, the fact that the meridians lose their curvature away from the equator somehow, at least to me, fairly shouts the idea of calculating the arithmetic mean of this projection with another kind of projection, perhaps the Aitoff, for example:
but while this projection does have a pleasing appearance, it still also looks strange, perhaps even more so than the Larrivée itself, because of its overall shape.
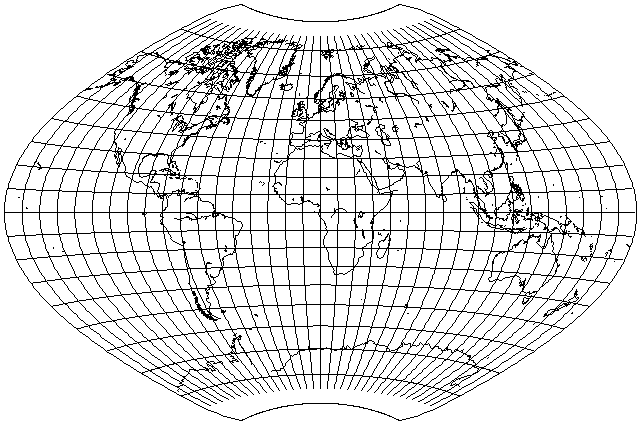
And, just for comparison, here is the world on the Savard Egg projection (a conventional projection, and thus a member of a different family) since it has a somewhat similar aspect ratio:
Well, it isn't quite as good, having somewhat more shear. But then it also has somewhat less areal distortion, although that could be taken care of in a projection of the type shown above by giving the Van der Grinten projection less weight.
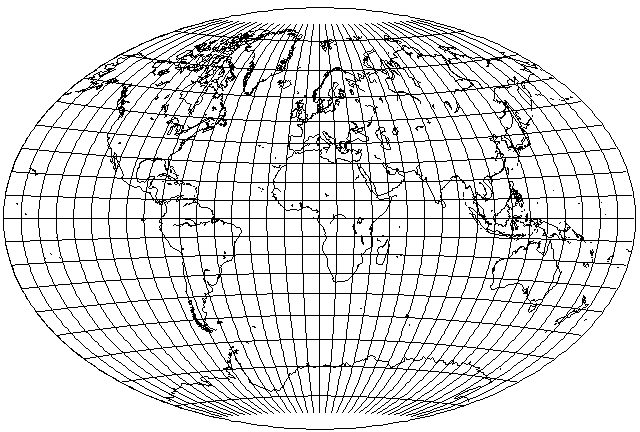
Of course, the Aitoff-Wagner projection itself has considerably less areal distortion, and it keeps shear down by means of its relatively long pole-line. If I can get away with making the pole-line a little shorter, as shown in the example with two scale factors of 0.8, I am happy to do that. "Craster's Minmum-Error Polyconic" is a projection which resembles projections of this type, but which is based on more sophisticated mathematics. And if the pole-line joins up with itself, one can meet the Laskowski Tri-Optimal projection, another attempt at a minimum-error projection of the whole world.
Using different ratios for the latitude and longitude, I shrank the longitude to 1/2 its value, with no further shrinkage, as in the Hammer, but shrank the latitude as well to 3/4 its value, with inverse stretchings of the x and y coordinates, to obtain:
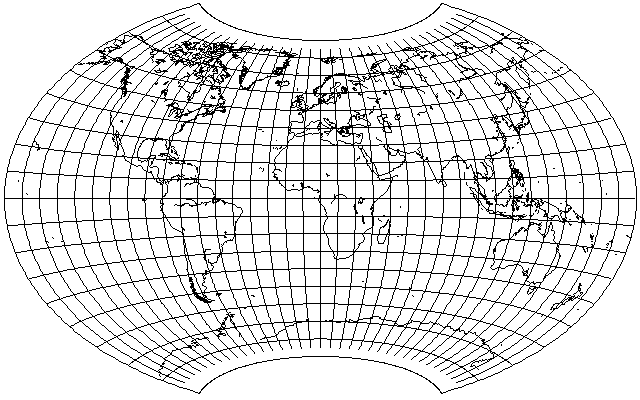
and then, applying a further stretch of the y coordinate of 7/6ths, I obtained the following:
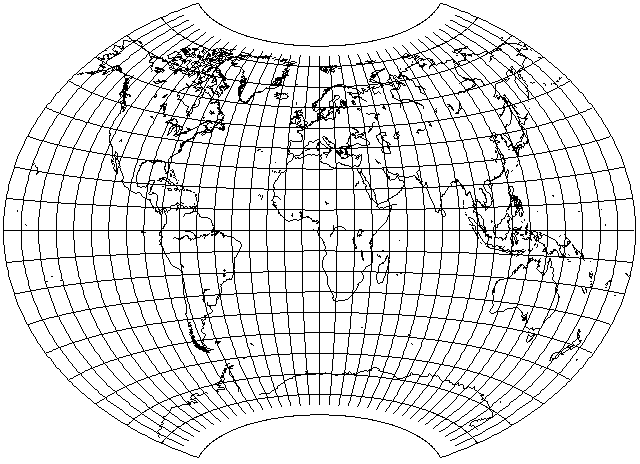
in an attempt to see if this was how Canters' Minimum-Error Polyconic projection worked, but it was not; apparently, that projection is instead based on a polynomial expansion, like the Laskowski Tri-Optimal.