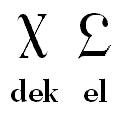
There are various features of our everyday world that are not as efficient as they might be, and from time to time, movements have sprung up to reform them which have not met with success.
People speak thousands of different languages, and thus have difficulty in talking to one another. Thus, Esperanto, and a few other languages as well, have been proposed as a single language for all humanity.
The layout of the typewriter leaves a great deal of room for improvement, which could permit greater typing speed. The Dvorak layout, as one proposed improvement, has met with some degree of recognition.
The calendar, since it starts on a different day of the week each year, could be simplified. One proposal, the World Calendar, has been noted in some popular works on timekeeping and in articles on the calendar in several encyclopedias. That proposal, however, involves including one or two days in the year that are not part of the seven-day week, which conflicts with the seriousness with which a number of faiths take Sabbath observance.
The spelling of the English language is irregular, and a number of people have advocated that we change over to a system of writing that comes closer to a phonetic transcription of our speech, so that learning to spell properly would not take years of memorization.
Another proposed reform that has occasionally been brought to the general public's attention in mathematics textbooks is the proposal to change how we write numbers: instead of counting things in tens and tens of tens and so on, it would be an improvement to count them in twelves and twelves of twelves and so on.
People are understandably reluctant to make the effort to learn something new when they already know something that works, even if the new thing might work even better. Thus, some reforms might have a chance to succeed if they can be largely taken up by the next generation.
The decimal system of numeration, however, is quite deeply ingrained, having been in use for some time. Thus, even if there were great benefits to be had, I would not be optimistic about the prospects for change.
And one number base works as well as any other in many ways; arithmetic can be performed in any base, and thus the choice of number base is generally regarded by mathematicians as nothing more than an arbitrary convention.
Computers, of course, can do arithmetic more efficiently in binary than in any other base. That might be considered an argument for us to switch to octal or hexadecimal to remove the need for conversion.
But what would be the benefit of switching to duodecimal?
If one thinks of the integers, of packing things ten to a box, and then packing ten boxes in a bigger box, and so on, it's hard to see that it makes much difference. Of course, we do pack twelve eggs to a carton, and twelve cartons to a box containing one gross of eggs, and using decimal notation to write the number of eggs in that box as 144 hasn't stopped us.
Other than the fact that 12 is 2 * 2 * 3, while 10 is 2 * 5, and so packing boxes in bigger boxes of twelve boxes might let us avoid elongated or otherwise oddly-shaped boxes, it's not immediately clear that a serious difference is made.
However, if one goes to the other side of the decimal point, it is a different story.
If one looks at a ruler with both a scale of inches and a scale of centimetres on it, the centimetres are marked off by tenths into millimetres, while the inches are usually marked off into sixteenths.
Sometimes, though, on half of the ruler, or on the other side, some of the inches are divided into tenths. And on some rulers, there are inches divided into twelfths as well.
So in going from inches to centimetres, the ability to divide things into thirds was lost; even dividing them into quarters isn't as easy as it was before.
Being able to divide things equally into 17 parts, or 13 parts, or 11 parts, or even 7 parts isn't all that important, but dividing things in half is very commonly desired, and the next most common division likely to be sought after is the one into thirds.
In comparision, dividing things equally into five parts is also fairly rare; our common use of the decimal system makes 5 seem to be a solid, ordinary number, but perhaps it's really only slightly less odd and strange than 7.
One could argue, but without too much solid foundation, that geometry itself teaches this, since triangles, squares, and hexagons neatly tile space, while pentagonal and heptagonal symmetry are only attainable in the exotic realm of things like Penrose tilings.
Ancient uses of measure that predated the metric system often use factors of two and three; twelve inches to a foot, three feet to a yard, two yards to a fathom; two pints to a quart, four quarts to a gallon.
Today, programmers are familiar with the use of the letters A through F to represent the values 10 through 15 as single hexadecimal digits. Before the IBM System/360 made this the universal standard, some early computers used alternate notations for hexadecimal:
10 11 12 13 14 15
System/360 A B C D E F
C a b c d e f
Bendix G-15, SWAC u v w x y z
Monrobot XI S T U V W X
Datamatic D-1000 b c d e f g
Elbit 100 B C D E F G
LGP-30 f g j k q w
ILLIAC k s n j f l
Pacific Data Systems 1020 L C A S M D
One could use A and B to represent the two extra digits needed for base-12 notation; or, given that X represents 10 in Roman numerals, and preferring to overload less-used letters, one might use X and Y for that purpose. But using letters in that way, while it makes sense when base 12 is only going to be used occasionally for purposes of illustration or other special purposes, would be inadequate if base 12 were going to be what was used every day for writing numbers.
I remember that, in introducing the concept of alternate number bases, the math textbook I used during one grade of junior high showed the shapes of two new digits proposed for duodecimal notation, named "dek" and "el". Recently, I found out where those came from, having found the web site of The Dozenal Society of America, formerly known as The Duodecimal Society of America. (Note how the new name avoids giving priority to the base-ten system.)
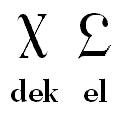
An important argument in favor of a base-12 system is that a system of weights and measures analogous to the metric system would have the desirable properties of traditional English measures, since anything made of whole units could naturally be divded into two, three, or four parts as a whole multiple of the next smaller unit.
In any event, it turned out those symbols were designed by the same W. A. Dwiggins who was responsible for such typefaces as Caledonia, Electra, and Metro.
The Dozenal Society used these digits in its publications for some time, but then changed over to using a pair of symbols based on the * and # characters found on the Touch-Tone telephone for a time. Recently, though, it changed back to them, noting at the time of the announcement that this was largely due to advances in the quality of digital document preparation which provided the additional flexibility needed. Another set of symbols for the two additional digits which has a significant degree of recognition is that devised by Isaac Pitman, where the symbols for the two additional digits are those for the numerals 2 and 3, each rotated by 180°; but many alternate systems of numerical notation have been proposed.
Isaac Pitman's proposal, of course, lent itself to letterpress printing, since instead of creating new symbols, all that would need to be done is put the type slug in upside down. And it guarantees that the resulting symbols will "look" like digits, a significant consideration. Excluding 0 for its symmetry, 1 and 8 for their near symmetry (depending, of course, on the typeface for its extent), and 6 and 9 for being reversals of each other, one could continue this principle to have reversed 2, 3, 4, 5, and 7 as additional digits; unfortunately, this is enough for base-15, but not for base-16, and so the need for some originality cannot be escaped.
The ampersand is available in nearly all typefaces, and so, starting from a monospaced yet print-like typewriter typestyle with serifs, I've also added in such letters as are not excluded by symmetry to produce:

which would be usable up to base 32, using sixteen of the letters after using 2, 3, 4, 5, and 7 and then the ampersand, all upside down.
I chose to use the ampersand first because, in addition to being available in nearly all typefaces, it tends to be generally curved, making it more digit-like than most letters.
The characters on a typewriter, though, don't lend themselves to being turned upside down. However, in the type specimen books in which one could find type for printing presses, there were both typefaces that simulated popular typewriters of the day, and another category of typeface, the "mailing list font", that would be suitable to this purpose.
Even with suitable fonts, however, another issue arises: there is space on the type slug below the baseline for descenders, but not an equal amount above the cap height, and so lining numbers and capital letters with their type slugs turned upside down would be lower on the line than their right-side-up versions. But paddng them with small pieces of leading would still be easier than cutting entirely new characters.
In his Mathematical Games column for May 1964 on the ternary number system, Martin Gardner mentioned that Joseph Bowden had advocated the use of a base-16 system, and had also invented new symbols for the digits it would use, illustrating those symbols in his book Special Topics in Theoretical Arithmetic, published in 1936. This book is apparently quite rare and hard to find, but a copy has been made available for viewing on the web, and so I can now depict here the digits which he designed:
![]()
He designed digits representing the numbers from 10 to 16. Why 16? We only need digits going up to 9 to write in base 10, and we only need digits going up to 15 to write in base 16. Well, from his book, the answer to that question happens to be readily apparent. He proposes several alternate numerical bases for consideration in a short discussion before settling on 16 as the best one; but in that discussion, he refers to each base by its single-digit symbol in his notation rather than by its expression in decimal notation - presumably to avoid a built-in bias favoring decimal notation.
And indeed, this book must have been hard to find. In my search for it, I turned up an article in a mathematical education magazine from Australia in which, in the absence of contact with the original work, but using as a basis the one digit Gardner did describe, that for 15, which is a reversed 5, made the reasonable hypothesis that the digits from 12 through 15 were represented by the reversed digits from 2 through 5. The author, Michael A. B. Deakin, then proposed the Russian letters "yu" and "i", the former looking like I and O linked by a short horizontal line, the latter like the letter N reversed, as symbols for the digits 10 and 11, no doubt based on their resemblance to the decimal numerals.
As well, in the Symbology issue of the bulletin of the Dozenal Society of America, published in 2010, where a large number of alternate notations, including at least a few for bases larger than twelve, were presented, it was not among those shown.
Also missing from there is a system devised by one John W. Nystrom, also known for having designed an unusual circular slide rule. Here, one of the existing digits of the decimal system is given a new value, the digits of his system being:
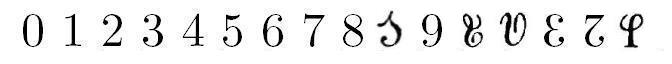
Of course, designing new symbols for the digits required by a different base notation only makes sense if that base were to replace the decimal system for ordinary purposes of numeration. When a different base is only resorted to for special purposes, 0123456789ABCDEF for hexadecimal, or, say, 0123456789XY for duodecimal, would be fully satisfactory.
And it does not seem that there would be any possibility, ever, of the decimal system being replaced by something else - despite the pull of binary from computers, or the attractiveness of duodecimal for ease of dealing with fractions, the importance of which is demonstrated by how many pre-metric systems of measurement were designed.
Still, the fact that 1,024 is very close to 1,000 has led to what might be called the "long kilobyte", thus bringing in binary units of quantity into ordinary conversation by stealth, as it were. I note elsewhere that there is little prospect of that for duodecimal, however.
The past existence of the decimal system means that fractions of fifths are at least sometimes important, which would tend to be an argument in favor of base 60, or at least base 30, instead of base 12, if it were felt necessary to express thirds as fractions exactly but not necessarily sevenths or elevenths. But base-60 or even base-30 require too many different digits to be considered practical. Of course, base-60 could be expressed as a mixed-radix notation.
Using two digits to represent a base-60 number, of course, is less dense, hence less efficient, than decimal notation.
I recently considered the idea of including both thirds and fifths with base-15 notation, and somehow appending a way to represent halves and quarters to the system. However, some thought led me to conclude there would be no practical way to do this. However, one could represent numbers in base 240 notation using alternating base-16 and base-15 digits; this would cover all the most popular fractions, while using only a reasonable number of digits, with a high information density.
I would put the base-16 digit first in each pair, as that would handle halves and quarters better as fractions, and it would be suited to our decimal habits of clumping things together by fives. Not that I can, of course, really propose this very seriously, but at least as it is a system with a consistent radix, calculations can be performed in it in a practical manner: doing them manually, though, would require learning two sets of multiplication and addition tables, one for even digit positions and one for odd digit positions.
This principle could even be taken to a ridiculous length by going from groups of two digits to groups of five digits: base 16, base 15, base 14, base 13, and base 11... so that terminating strings of digits past the radix point could represent fractions in any denominator composed only of the primes 2, 3, 5, 7, 11 and 13. But that, at least, is clearly both very complicated and without much, if any, practical application.
Instead of using pairs of digits in base 16 and base 15 to use 240 as one's number base, one could also be less radical and use pairs of digits in base 12 and base 10 so as to use 120 as the number base.
Further thought has led me to reconsider the possibility of a "stealth" base change similar to what has happened with binary quantities of RAM and disk space. 120, after all, is not too far from 128. Multiply that by eight, and one gets 960, which is close to a thousand.
If one makes a second substitution of 15 for 16, one gets 900. And base 900 notation could be achieved using the ordinary decimal digits. Thus, in each group of three digits, the middle one could be base-9, going only from 0 to 8.
In this system of notation, many fractions could be represented exactly; for example, here is how the twelfths would appear:
11/12 .915 5/6 .83 3/4 .745 2/3 .66 7/12 .575 1/2 .5 5/12 .415 1/3 .33 1/4 .245 1/6 .16 1/12 .075
However, since 90 * 90 = 8100 in decimal, in this system 100 * 100 = 9000. Thus, having just two multiplication tables is not enough - and some further reflection led me to realize that long division in this system would be a nightmare.
But then I realized that there was hope. 900 is, after all, the square of 30.
Octal and hexadecimal, when used with computers, can be viewed as a convenient notation for the underlying system of binary.
And so this scheme of number representation, which consists of groups of three digits, base 10, base 9, and base 10, could be viewed simply as a convenient way to represent numbers that are in base 30, and which could be converted to their true base 30 form before performing arithmetic operations more involved than addition and subtraction.
That would be carried out like this:
872,945,263
8 7 2 9 4 5 2 6 3
8 2 1 2 9 1 1 5 2 2 0 3 (1)
2 6 1 2 2 8 1 5 0 8 0 3 (2)
26 12 28 15 8 3
In step (1), the middle digit of each group of three digits is converted to a pair of base-3 or ternary digits.
In step (2), the first half of each group of three digits is converted from den-trinary representation to tri-denary representation, to match the way the second half is represented.
And the result is the digits, represented as decimal numbers, of the base-30 form of the original number.
Thus, if base-30 long division is practical, long division of numbers in this format is practical as well, as they can be easily converted to base 30.