

Pi, the ratio of the circumference of a circle to its diameter, is 3.14159 26535 89793... to 15 decimal places.
It is, roughly, 3 1/7, or 22/7. A better fractional approximation is 3 16/113, or 355/113. The latter approximation, 355/113, was first discovered by the Chinese astronomer and mathematician Tsu Ch'ung-chih (Zu Chongzhi) in the fifth century. In the West, it was discovered in 1585 by Adriaan Anthonisz, and first published in 1625 by his son, Adriaan Adrianszoon, better known as Peter Metius.
Other mathematical constants, such as the base of the natural logarithms, e, 2.71828 18284 59045..., or Euler's constant, 0.57721 56649 01532..., are almost always used as is in mathematical formulas, but many formulas involving pi use instead either 2*pi or pi/2.
The earliest known use of pi to represent the circle ratio was by William Jones in Synopsis Palmariorum Mathesos; or, a New Introduction to the Mathematics, and that notation became generally popular due to the use of that symbol by Euler.
Recently, it has been proposed that we should use 2*pi as the fundamental constant instead, represented by the Greek letter tau, so as to make understanding some initial steps in the geometry of circles more obvious; and then someone later suggested that, as it is easier to multiply than divide, that instead we should use pi/2 as the constant, represented by the Greek letter eta.
While I think it's much too late to change, it could well be that an alien technological civilization could have indeed used either of those two alternate values as the fundamental value of the circle ratio, and so they might not be looking for a signal sent at a frequency of pi times the 1420.40575 MHz emission line of interstellar hydrogen.
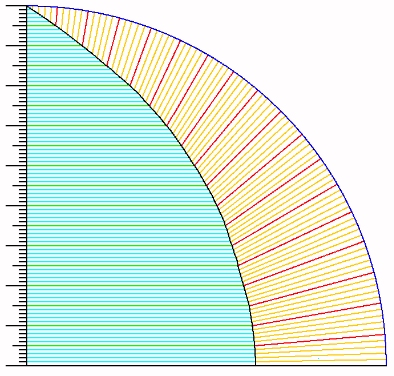
As the area of a circle is pi times the square of its radius, the ratio of the side of a square to the diameter of a circle with the same area is one half of the square root of pi.
This value is about 0.88622 69254 52758..., again, to 15 decimal places.
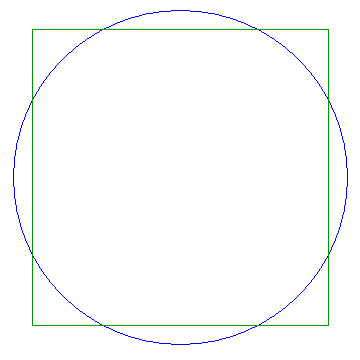
An approximation to this value used by the ancient Egyptians, as recorded in the Rhind papyrus by the scribe Ahmes, is 8/9. A better rational approximation to this value is 148/167, and the diagram to the left, showing a circle, and a square equal to it in area, as closely as can be drawn in discrete pixels in a diagram of reasonable size, uses this approximation.
Incidentally, if one squares 148/167, and then multiplies by four, one gets the approximation for pi 3.14159704543..., whereas 355/113 is 3.1415929203539823..., and, so, since pi is 3.14159 26535 89793..., the latter is over 16 times as close an approximation to pi (the ratio of the differences works out to 16.46338...) and it is correct to one additional decimal place as a result.
While the circle can't be squared using a straightedge and compasses in a conventional manner, just as the angle can't be trisected that way (although there is a construction, known to the ancient Greeks, that used a straightedge and compass somewhat unconventionally that does trisect it) the value of pi can certainly be calculated, and calculating pi can be termed "squaring the circle".
In the case of squaring the circle, the rule that has to be broken is the one requiring a construction to be done in a finite number of steps. Here is the Quadratrix of Hippias:
at least a crude sketch of it I made by hand. The principle of that curve should be obvious from the diagram; it contains those points that have the same proportion in height as they do in angle. Since one can bisect an angle and a line with straightedge and compasses, one can use them to make as many points as one wishes on this curve, with as close a spacing as desired.
But that does not mean that one can draw certain exact points on that curve that one might want, such as the one where it crosses the horizontal line through the center of the circle, the distance of which from the center of the circle being exactly 2/pi times the radius of the circle.

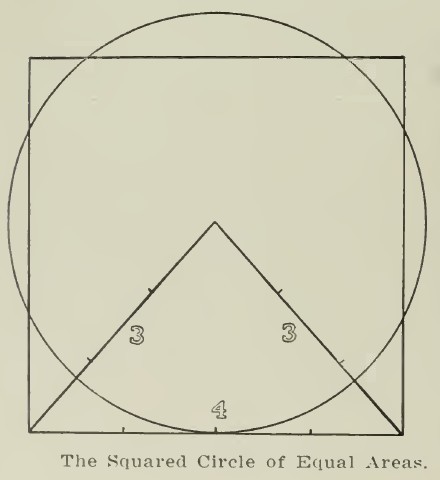
An example of a fallacious attempt to square the circle, in this case from a book by an occultist rather than a circle-squaring mathematical crank, is shown at right. The cover of the book is shown at left.
Although the cross featured prominently on the cover is the ancient Egyptian ankh, also known as the crux ansata, in the body of the book, the cross to which the most space is devoted is the swastika. However, this is innocent enough, given that the book dates from the year 1912.
In any case, from the Pythagorean Theorem, it's simple enough to determine from the diagram that the radius of the circle is supposed to be the square root of five. Given that the area of a circle is pi times the radius squared, this means that the area of the circle here is five times pi, which is about 15.70796..., which falls short of the area of the square, which is 16.
Later in the book, there is a "squared circle of equal perimeter" which is explicitly stated to be approximate, where the sides of the triangle are 4 and 5 instead of 3 and 4, so I have to think that the author mistakenly thought that this earlier diagram did indeed exactly square the circle.
A better approximation would have been to give the triangle sides of 5197 and 8768 instead of 3 and 4.
The book includes a picture of the author;

Behind the author appears to be an assistant with a typewriter, just what J. R. R. Tolkien was unable to afford; to the right of the image is a pile of books and a teacup with something leaning on them. Despite the resemblance, no doubt it is not a cell phone.
Pi is defined as the radius of the circumference of a circle to its diameter, but it's also used in the formulas for the area of a circle and the volume of a sphere. To start with, let's see how those formulas could be derived.
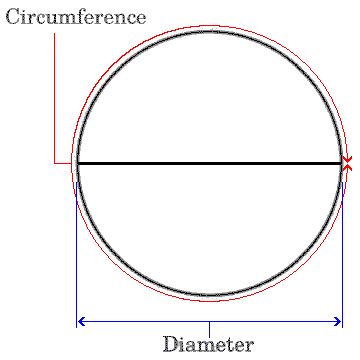
The definition of pi is the ratio of the circumference of a circle to its diameter. The circumference of a circle is the length of the curved line which constitutes the circle itself, and the diameter of a circle is how wide it is at its widest part. Since circles are round, and thus the same in all directions, it's also how high it is at its tallest part, and so on for any direction.
Pi is also used for calculating the area of a circle, the area of the surface of a sphere, and the volume of a sphere.
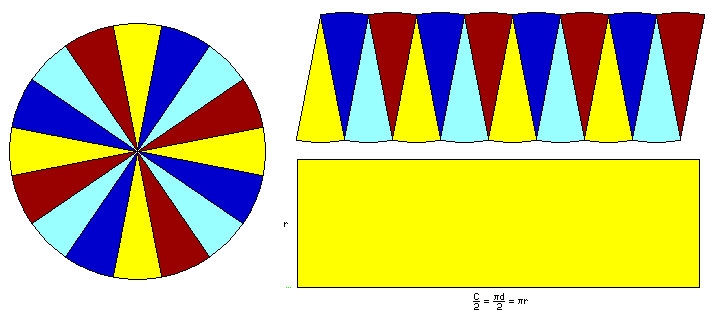
The diagram above is an attempt to justify the formula for the area of a circle, A = pi * r^2. This kind of diagram can be found in many mathematics textbooks, and one was included in a book by Sato Moshun, in Japan, in 1698; also, an illustration of the same idea appears in the Notebooks of Leonardo da Vinci.
Basically, one can cut the circle into more and more slices, and as one does so, the shape that can be built by rearranging those slices gets closer and closer to a rectangle with the radius of the circle as its height, and half the circumference of the circle as its width.
This made ancient diagrams like this particularly notable, since the idea of a limit of an estimate of the area of a shape by cutting it into smaller and smaller pieces is a basic idea that led to the integral calculus.
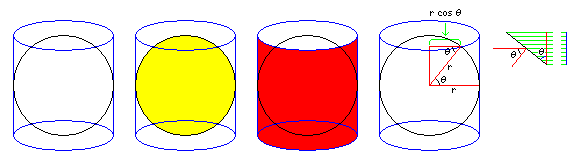
It was Archimedes of Syracuse who found that the surface area of a sphere is the same as that of the curved surface of a cylinder with the same diameter and the same height - just the curved surface, not including the flat top and bottom.
Why this is the case is illustrated by the diagram: the cosine of the angle theta both determines the size of a circle at a given height of the sphere, and the amount vertical distances on the sphere's surface are foreshortened when projected on the surrounding circle.
This is the basis, incidentally, of an equal-area cylindrical map projection, which I describe on this page.
So, since the surface of the cylinder can be unrolled into a rectangle with a height equal to the sphere's diameter, and a width equal to the sphere's circumference, the surface area of a sphere is equal to pi * d^2, or 4 * pi * r^2.
Just as a circle can be cut into many tiny pie wedges, a sphere can be thought of as many tiny little pyramids, with a height equal to the radius of the sphere, and the bases of which total in area to the surface area of the sphere.
This would tell us the volume of a sphere, now that we know the formula for the surface area of a sphere, if we knew how to calculate the volume of a pyramid.
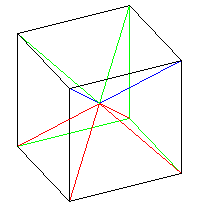
The volume of a pyramid is one-third of the area of its base times its height.
So the volume of a sphere is (4/3) * pi * r^3.
Why the volume of a pyramid is exactly one-third of the product of its base and height can be illustrated the most simply by the diagram above. A cube has six faces, as anyone who has ever played a game with (conventional!) dice knows: and its volume can be divided into six pyramids, with bases having an area equal to the side of the cube squared, and a height equal to half the height of the cube.
And, of course, one-sixth is one-half of one-third.
One of the basic facts about pi is that it is a transcendental number.
I'd like to say a few words about what that means.
The most basic numbers are the integers; we get those by counting objects one after another. Now, there are negative integers, and yet you can't hold -3 pebbles in your hand; extending the number system in this direction leads to the imaginary numbers, which raise a different kind of question, so I will put that aside here.
Instead, the next step is the rational numbers; that is, fractions that have an integer as both the numerator and the denominator. When, instead of counting objects, we measure out liquids, or we measure out lengths, or set up systems of units to use in these measurements, we usually use fractions like this.
Since integers can go as big as we like, we can get as close as we like to any desired volume, weight, or distance with a rational number. So from one kind of practical viewpoint, the rational numbers are all we need.
However, the relationships and formulas that are found in mathematics are useful for many practical purposes, and to derive them, we have to be able to think of numbers and points and lines and shapes in an abstract manner, dealing with their exact values and positions, without concern for the limitations of the real world that often mean that a good approximation is as good as we'll either need or be able to get.
One of the simplest numbers that isn't rational is the square root of two - the length of the diagonal of a square of length one.
It's easy enough, starting with a line of unit length, to draw a square with sides all of that length, in a finite number of steps, using a straightedge and compass strictly in the conventional manner. And that lets you then draw the diagonal and copy it.
So the square root of two is what is called a constructible number. These numbers are those which can be produced from integers by addition, subtraction, multiplication, division, and taking square roots. This includes fourth roots or eighth roots or sixteenth roots, because one can take square roots repeatedly.
One thing that can't be done in a finite number of steps, using a straightedge and compass strictly in the conventional manner, is to trisect the angle. But if you do something sneaky, for example, holding your compass against the straightedge to indicate a length along it, while you move the two tools into position, then you can trisect the angle: Archimedes first found this construction, and I remember seeing an elaborate version of that construction featured in the letters column of Mechanix Illustrated.
But while ingenuity like that of the television character MacGyver certainly has its uses, it's also useful to have a category for the numbers that can be made with straightedge and compass in a pedestrian fashion.
One of the other famous problems that was not solvable with straightedge and compasses was the "Duplication of the Cube", that is, given a line of unit length, drawing a line that is the cube root of two times as long.
So the next level above constructible numbers are those numbers that are expressible by radicals. The numbers that can be produced from integers by addition, subtraction, multiplication, division, and taking the n-th root for any integer n are also a group of numbers that are closed under that set of operations.
If you try to solve a quadratic equation, you can use the formula that the equation a*x^2 + b*x + c = 0 is true if x equals either (-b+sqrt(b*b-4*a*c))/(2*a) or (-b-sqrt(b*b-4*a*c))/(2*a). So the roots of a quadratic equation are numbers that are expressible by radicals.
Formulas were also found, but more complicated ones, to solve the cubic equation, where x^3 is also present, and the quartic equation, which also has x^4, too.
But a famous event in the history of mathematics was the proof that the quintic equation didn't always have solutions that were expressible by radicals. x^5 = 7 has the fifth root of 7 as its solution, so some quintic equations do have such solutions - but the equation x^5 + x + a = 0 does not.
Numbers which are the solutions of equations of the form a*(x^n) + b*(x^(n-1)) + c*(x^(n-2)) + ... z = 0, starting with any n, however large, where all the coefficients a, b, c... are rational numbers, are called algebraic numbers.
But even the algebraic numbers don't cover all the possible values for such things as a distance along a line. The circumference of a circle of unit diameter, which is pi, the number we are talking about, is one of those numbers that isn't algebraic, and that means it is called a transcendental number. The first proof that pi was transcendental was due to Lindemann in 1882.
Archimedes is the first person known to have derived the value of pi by means of mathematical reasoning. Using polygons of 96 sides, one enclosing the circle, and one enclosed by the circle, he established that pi was less than 3 1/7, but greater than 3 10/71 in his work Measurement of the Circle. He was credited by Heron of Alexandria with having subsequently improved those bounds, proving that pi was less than 195882/62351 but greater than 211872/67441 (these figures are, in fact, a modern guess at what was meant, as at least in the copies of Heron that we have, they are garbled); this was in a lost work with the title Plinthides and Cylinders.
Many years later, also using polygons and geometry, Ludolph van Ceulen calculated the value of pi to 34 decimal places. Numerous references state that because of this, pi became generally known as the Ludolphine Number (Ludolphische Zahl) in Germany; thus, for example, it appeared in the title of an 1885 paper by Weierstrass; however, that term was most popular prior to 1910, and was much less common in Germany in the postwar era.
This method of calculating pi was difficult, but at first it was the only valid mathematical method known. Eventually, as a consequence of the development of calculus, it became understood how to easily develop Taylor series for the various elementary functions, but the arctangent series was developed before the invention of calculus.
The earliest mathematical formula for pi was that derived from how it might be calculated geometrically with polygons (starting from a square, rather than from a hexagon as Archimedes did) by François Viète:
pi 2 2 2 ---- = --------- * ------------------- * ----------------------------- * ... 2 sqrt(2) sqrt(2 + sqrt(2)) sqrt(2 + sqrt(2 + sqrt(2)))
This is a somewhat modernized form of his formula, not in the exact form he originally gave. The same is true for the infinite product given by John Wallis in 1650:
pi 2 * 4 4 * 6 6 * 8 ---- = ------- * ------- * ------- * ... 4 3 * 3 5 * 5 7 * 7
The power series for the arctangent function, which can be used to calculate pi, is as follows:
3 5 7
x x x x
atn(x) = --- - ---- + ---- - ---- + ...
1 3 5 7
This series is known as Gregory's series, after James Gregory, who discovered it in 1671; not until much later did Western mathematicians learn that it was discovered by Madhava of Sangamagrama more than 250 years previously.
Since the arctangent given by this series is in radians, the arctangent of 1 is equal to one-quarter of pi. That, however, is a value for which this series converges at an extremely slow rate, so slow as to be useless in practice as a way to calculate pi. For x less than 1, however, it converges at an acceptable rate, faster as x becomes smaller.
If it is being used in an arctangent function, for x greater than one, one would calculate the arctangent of 1/x and subtract that from pi/2, as the series does not converge for x greater than one. For values of x close to 1, either above or below it, say between 1/2 and 2, another transformation so that the angle away from pi/4 would be calculated instead would be used in practice. But today techniques like CORDIC would be used instead, as they are faster. None of these techniques help in calculating the value of pi, however.
One way to use a value less than 1 as the input to the arctangent series and yet produce a result that does lead to a value for pi would be to use the fact that 30 degrees, or, in radians, one-sixth of pi, is the arcsine of 1/2. The Pythagorean theorem can be used to determine that the arcsine of 1/2 is also the arctangent of one over the square root of three.
Since the terms of the arctangent series involve powers of x that are multiplied by x squared at each step, one can do the calculation only using whole numbers until you multiply in the square root of three at the very end. This was how pi was calculated by Abraham Sharp in 1699 to 71 digits.
Isaac Newton, one of the two independent inventors of the calculus, derived the arcsine formula in 1676:
3 5 7
1 x 1 * 3 x 1 * 3 * 5 x
arcsin(x) = x + --- * --- + ------- * --- + ----------- * --- +...
2 3 2 * 4 5 2 * 4 * 6 7
and he used it to calculate pi to at least 15 digits from the fact that pi/6 is the arcsine of 1/2.
Incidentally, pi/10 is the arctangent of sqrt(5 - (2/5) * sqrt(5)) and the arcsine of sqrt(1 + sqrt(5))/4, which latter figure is one half of the golden ratio. This has more to do with the relationship between the golden ratio and the pentagon than any relationship between it and pi, of course.
Because it is possible to construct a 17-sided polygon by straightedge and compasses, there are also expressions involving the square root of 17 that could also be used in this fashion.
It would be more convenient, however, if a simpler quantity not involving a square root, and significantly smaller than 1, could be used in the arctangent formula, because that would lead to a series that would converge more quickly even than the arcsine formula for x=1, let alone the arctangent formula for that value.
While no single rational value of x between 0 and 1 has an arctangent that is a rational multiple of pi, if one is willing to evaluate the arctangent function two or more times, this simplification can be obtained.
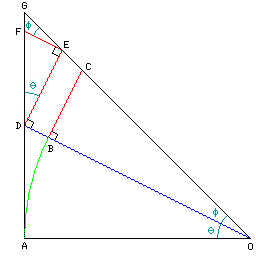
The diagram to the right illustrates how one can calculate, given the tangents of two angles, the tangent of the sum of those angles.
Let the length of the line segment from A to O be equal to 1.
Then, the length of the line segment from A to D is the tangent of the angle theta;
as the length of the line segment from B to O also equals 1, the length of the line segment from B to C is the tangent of the angle phi;
and the length of the line segment from A to G is the tangent of the angle theta plus phi.
Let us denote the tangent of theta by P, the tangent of phi by Q, and the tangent of theta plus phi by R.
From the Pythagorean theorem, we know the length of the line segment from D to O is equal to the square root of P squared plus 1. And therefore the length of the line segment from D to E is equal to Q*sqrt((P^2)+1).
Given that the angle FDE is also theta, the same ratio is applied a second time, and the length of the line segment from D to F is equal to Q*((P^2)+1).
While the small triangle that remains to be understood in order to work out the length of the line segment from F to G which remains is not a right triangle, it could be broken into two pieces that are right triangles. However, it is apparent at this point that we're not taking quite the right approach, and we need to change one thing in the diagram.
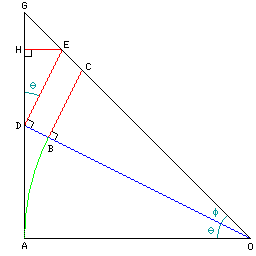
In this diagram, ignoring the point F, and instead paying attention to a new point, H, this time, as the right triangle is turned around, the length of the line segment from D to H is simply Q.
The remaining triangle is now a right triangle. But the angle GEH is neither phi nor theta, it's phi plus theta, and the tangent of that is what we want to calculate from P and Q. Are we in trouble?
No, we aren't. The length of the line segment EH is clearly equal to P times Q. The ratio of P plus Q to 1 minus P*Q is equal to R. One can drop a perpendicular from E down to the line segment AO to make it obvious how this conclusion can be reached: since the ratio of the lengths of the line segments HG and HE is the arctangent of theta plus phi, just as the ratio of the lengths of the line segments AG and AO is the same value, a triangle, smaller in size by the factor (1-(P*Q))/1 can be formed in which the ratio of P+Q to 1-(P/Q) can be seen to be R.
One example, due to Euler, and based on which these diagrams were drawn, is that atn(1) = atn(1/2) + atn(1/3). So if 1/2 = tan(theta) and 1/3 = tan(phi), tan(theta+phi) is 5/6 divided by (1 - (1/2)*(1/3)), which is 5/6 divided by itself, or 1.
Applying this formula repeatedly, though, it becomes possible to obtain even better results.
So that we could use something that converges even faster than powers of 1/2, could it be that if we solve atn(1/2) = atn(x) + atn(1/3), we would have something useful as x; that way, we wouldn't have to calculate the arctangent three times, we could just multiply atn(1/3) by two.
As it turns out, x equals 1/7, since 1/2 is 10/21 divided by (1 - (1/3)*(1/7)) or 20/21.
If atn(1/2) = atn(1/7) + atn(1/3), then it's also true that atn(1/3) = atn(1/2) - atn(1/7).
Thus, we now have pi/4 = atn(1) = 2*atn(1/3) + atn(1/7), which is an improvement, since atn(1/3) converges more quickly than atn(1/2).
So we can subtract arctangents as well as adding them.
This led to the formula pi/4 = atn(1) = 4*atn(1/5) - atn(1/239), derived by John Machin in 1706, which was used for a number of attempts to calculate pi to a large number of digits.
For example, it was used for two of the earliest calculations of pi on a computer, one to 2037 places on the ENIAC by Reitweisner in 1949, and one to 3089 places on the NORC by Nicholson and Jeenel in 1954.
From 1873 to 1945, it was believed that the value of pi was known to 707 digits, having been calculated to that precision, also using Machin's arctangent relation, by William Shanks. In 1945, calculations by D. F. Ferguson established that only the first 527 digits of that value were correct; his first calculations were made with pencil and paper, but he later used a mechanical calculator to help him to derive 808 digits in 1947. While there was a mistake in the value he initially had published in March 1947, in September 1947 he corrected the error.
Originally, when I first wrote this page, I thought that the error was not the fault of William Shanks alone. In 1853, he had published an earlier calculation of pi to 607 decimal places which, also being correct only to the first 527 places, contained the same error that marred his later calculation. This publication was in the form of a book which included each of the terms in the two arctangent series used for the calculation, making it much easier to check portions of the calculation for error than it was to make the calculation in the first place. However, those individual terms were only given to 530 places, not to 607 places. That still left open a possibility of other mathematicians finding the error, since this was three places beyond where it occurred, but it clearly makes the situation different than it would have been had that not been the case.
Another mathematician did check William Shanks' calculation as far as the first 405 (or 440?) digits. Ironically, the mathematician who did so was William Rutherford, who himself, in 1841, had published a value of pi to 208 digits which was correct only to the first 152 digits. That value, however, was soon corrected, in 1844, through a calculation carried out by Zacharias Dase.
A document by Erwin Engert, dated January 1, 2012, is available on the Web, which sorted out typographical errors in published versions of Shanks' 707 digits of pi, and which investigated where the error was made. Later, an article in American Scientist by Brian Hayes, in their September-October 2014 issue, continued the analysis, finding additional details of the errors, but not all the discrepancies have been accounted for, so it is not yet possible to re-calculate the erroneous value of pi that Shanks would have produced to more places.
Doing so might be of interest for this reason: his 707 digits of pi contained the digit 7 less often than might be expected from random chance, unlike the actual value of pi, which so far has given no indication that its digits are not statistically like a random sequence. If this anomaly were to continue in subsequent digits, it might provide an insight into the conditions under which a mathematical transcendental number like pi could have a digit sequence that is not normal.
Although faster methods for computing pi to a large number of places are now known, arctangent formulas have continued to be used in the calculation of pi even fairly recently.
The calculation of pi by D. F. Ferguson to 808 digits in 1947 in which a desk calculator was used was done using the following identity:
atn(1) = 3*atn(1/4) + atn(1/20) + atn(1/1985)
After the calculations on the ENIAC and the NORC used Machin's identity, a calculation of pi to 10,021 places on the Ferranti Pegasus computer by G. E. Felton used the identities
atn(1) = 8*atn(1/10) - atn(1/239) - 4*atn(1/515)
atn(1) = 12*atn(1/18) + 8*atn(1/57) - 5*atn(1/239)
In the first identity, the first term, being atn(1/10) instead of atn(1/5), is both faster-converging and more convenient for decimal calculations than the first term of Machin's series, and the remaining two terms converge very quickly. The second identity, due to Gauss, used for checking the result, was used again in a later calculation to be mentioned below.
One of the most recent such calculations was in 2002, undertaken by Yasumasa Kanada, in which he had a computer calculate pi to over one trillion digits, using the following two arctangent relations:
atn(1) = 44*atn(1/57) + 7*atn(1/239) - 12*atn(1/682) + 24*atn(1/12943)
atn(1) = 12*atn(1/49) + 32*atn(1/57) - 5*atn(1/239) + 12*atn(1/110443)
Because atn(1/57) and atn(1/239) occur in both relations, but multiplied by a different amount, errors for them would still make the two results disagree, and yet labor - or, rather, machine time - can be saved as these values need only be calculated once.
The second identity was found by F. C. W. Störmer in 1896; the first one by Kikuo Takano in 1982, who had used these same formulas himself for calculating pi to a lesser number of digits.
This basic technique was also used earlier, in 1961, by Daniel Shanks and John W. Wrench to calculate pi to 100,265 places on an IBM 7090 computer. Daniel Shanks, an American, is not known to have any relation to William Shanks.
They used the identities:
atn(1) = 6*atn(1/8) + 2*atn(1/57) + atn(1/239)
atn(1) = 12*atn(1/18) + 8*atn(1/57) - 5*atn(1/239)
so again the calculation could be checked even though atn(1/57) and atn(1/239) were only calculated once.
Here, Störmer found the first of the two identities used, and the second one was due to Gauss.
As noted, faster methods of calculating pi were discovered later.
The following series for 1/pi was discovered by the enigmatic Srinavasa Ramanujan:
infinity
_________
\
2 * sqrt(2) \ (4*i)! (1103 + 26390 * i)
----------- * > -------------- * --------------------
9801 / 4 (4*i) (4*i)
/________ (i!) *4 99
i = 0
Yes, 4^(4*i) and 99^(4*i) could be combined to form 396^(4*i); also, 9801 is the square of 99. so this formula can appear in other forms. It was used by R. William Gosper to calculate pi to over 17.5 million digits in 1985. A different series belonging to this class was used by the Chudnovsky brothers, and it has since been used in other calculations for pi:
infinity
__________
\
\ i (6*i)! 13591409 + 545140134 * i
12 * > (-1) * --------------- * --------------------------
/ 3 ((3*i) + (3/2))
/_________ (i!) * (3*i)! 640320
i = 0
again, this is a series for 1/pi.
The denominator of the second factor involves operations such as taking the cube and the square root of 640320 that don't have to be repeated for each term of the sum. Since 640320 is 320 * 2001, 320 being 64 * 5 and 2001 being 3 * 23 * 29, this leads to:
infinity
__________
\
1 \ i (6*i)! 13591409 + 545140134 * i
---------------------- * > (-1) * --------------- * --------------------------
426880 * sqrt(10005) / 3 i
/_________ (i!) * (3*i)! 262537412640768000
i = 0
and it also appears in this form or similar forms in addition to the original form which is somewhat shorter to write, if not to calculate.
How these series are derived involves a number of topics of mathematical interest, as noted in the Wikipedia article on Ramanujan-Sato series.
Series for 1/pi of the type discussed above yield a large number of digits of pi at each step; but since the same number of digits of pi are produced at each step, it might be possible to equal their performance with a suitably-designed arctangent relation in which all the arguments to the arctangent function are sufficiently small numbers.
Recurrence relations are now known, however, that double, triple, quadruple, or more, the number of digits calculated at each step.
The first such relation to be discovered was found by Eugene Salamin and Richard Brent in 1976; they both discovered it independently around the same time.
To find pi by this method, follow this recurrence relation:
a(0) = 1 b(0) = 1/sqrt(2) s(0) = 1/2 a(n+1) = (a(n)+b(n))/2 b(n+1) = sqrt(a(n)*b(n)) s(n+1) = s(n) - (2^(n+1)) * (a(n+1)^2 - b(n+1)^2)
and after iterating it as many times as required to obtain the precision sought, the approximate value of pi will be 2 * (a(N)^2)/s(N).
This recurrence relation includes the process of taking the arithmetic-geometric mean of a and b. While this method of calculating pi was only discovered in 1976, a recurrence relation involving the arithmetic-geometric mean was long known and used for calculating complete elliptic integrals.
For that purpose, this recurrence relation is applied:
a(0) = 1 b(1) = cos(t) a(n+1) = (a(n)+b(n))/2 b(n+1) = sqrt(a(n)*b(n))
and then K(t) is approximated by pi/(2 * a(N)), where N is the number of iterations taken to achieve the desired precision.
E(t) can also be determined, from the formula
infinity
________
K(t) - E(t) 1 \ i
------------- = --- * (sin(t) + > 2 * c(i)^2 )
K(t) 2 /_______
i = 1
where c(i) is defined as (1/2) * (a(i) - b(i)).
Sometimes, the form of the expression is simplified by defining c(0) as sin(x), although that doesn't correspond to the definition of c(i) for other values of i, so that the sum can start from i=0 without an additional term.
In these formulas, t represents the modular angle, often noted by the Greek letter alpha; the argument of the elliptic integral may also be the parameter, noted by the letter m. They are related by m = (sin(t))^2.
Later, a number of improved recurrence relations for pi with even faster convergence were developed by Jonathan and Peter Borwein and others; they developed algorithms which tripled, quadrupled, quintupled, multiplied by seven, and multiplied by nine, the number of correct digits at each iteration. Here is the one that multiplies the number of correct digits by nine at each step:
a(0) = 1/3 r(0) = (sqrt(3) - 1)/2 s(0) = (1 - (r(0)^3))^(1/3) t(n+1) = 1 + 2*r(n) u(n+1) = (9 * r(n) * (1 + r(n) + r(n)^2))^(1/3) v(n+1) = t(n+1)^2 + t(n+1)*u(n+1) + u(n+1)^2 w(n+1) = 27 * (1 + s(n) + s(n)^2)/v(n+1) a(n+1) = w(n+1)*a(n) + ((3^(2*n - 1)) * (1 - w(n+1))) s(n+1) = (1 - r(n))^3 / ((t(n+1) + 2 * u(n+1)) * v(n+1)) r(n+1) = (1 - s(n+1)^3)^(1/3)
The result of this computation is that a(N) is the approximation to 1/pi that improves at this large rate.
Here are the other relations of this type that are known:
the one that triples the number of correct digits at each step is:
a(0) = 1/3 s(0) = (sqrt(3) - 1)/2 r(n+1) = 3/(1 + 2 * ((1 - s(n)^3)^(1/3))) s(n+1) = r(n+1)/2 a(n+1) = (r(n+1)^2 * a(n)) - 3^n * (r(n+1)^2 - 1)
Here, a(N) is the improving approximation to 1/pi.
the one that quadruples the number of correct digits at each step is:
a(0) = 6 - 4*sqrt(2) y(0) = sqrt(2) - 1 y(n+1) = (1 - (1 - y(n)^4)^(1/4))/(1 + (1 - y(n)^4)^(1/4)) a(n+1) = a(n) * (1 + y(n+1))^4 - 2^(2*n + 3) * y(n+1) * (1 + y(n+1) + y(n+1)^2)
Once again, a(N) is the improving approximation to 1/pi.
the one that quintuples the number of correct digits at each step is:
a(0) = 1/2 s(0) = 5 * (sqrt(5) - 2) x(n+1) = (5/s(n)) - 1 y(n+1) = (x(n+1) - 1)^2 + 7 z(n+1) = ((1/2) * x(n+1) * ( y(n+1) + sqrt( y(n+1)^2 - 4*(x(n+1)^3) ))^(1/5) a(n+1) = s(n)^2 * a(n) - (5^n) * ( (s(n)^2 - 5)/2) + sqrt( s(n) * (s(n)^2 - 2*s(n) + 5) ) s(n+1) = 25/( (z(n+1) + (x(n+1)/z(n+1)) + 1)^2 * s(n) )
and, again, a(N) converges to 1/pi.
The one that multiplies the number of correct digits by seven at each step also requires evaluating a trigonometric function to the same high precision as is desired for the approximation to pi, and thus only provides a gain in efficiency if a similarly fast algorithm for calculating the cosine is known. Another algorithm which also multiplies the number of correct digits by seven at each step required a trigonometric function to be evaluated in every step.
Thus, the quintic and nonic algorithms appear to be the most rapid ones available, although there may also be one that multiplies the number of correct digits by sixteen at each step.
The algorithm developed by Brent and Salamin was the one used in 2009 for a calculation of pi to over 2.5 billion digits by a team led by Daisuke Takashi on the T2K Open Supercomputer. This was the last record-setting calculation of pi done on a large, expensive computer: subsequent ones have been done by private enthusiasts on commodity hardware.
The first of these was one to almost 2.7 billion digits by Fabrice Bellard later in 2009. All subsequent ones, in addition to using commodity hardware, also used the y-cruncher software written by Alexander Yee. Surprisingly, although this meant the calculations took longer, many of them were done using the Chudnovsky series, with a second faster iterative calculation being performed only for verification, instead of using two different iterative calculations.
While deriving these fast methods of calculating the value of pi is an impressive accomplishment concerning the computation of pi, this is not the most famous accomplisment of the Borwein brothers in connection with calculating pi.
Incidentally, their father, David Borwein, is also a noted mathematician. He was born in Kaunas, Lithuania, in 1924, but was taken by his parents to South Africa in 1930. In 1948, he moved to London, where his graduate studies took place; from 1963, when he initially came to Canada as a visiting professor, he lived in Canada where he held a number of distinguished posts, including that of the head of the mathematics department of the University of Western Ontario and that of the President of the Canadian Mathematical Society. His own mathematical work dealt with classical analysis, including such things as the summability of integrals.
Jonathan Borwein passed away unexpectedly and suddenly in 2016 at the age of 65 of natural causes, and was survived by his father as well as his brother Peter.
Jonathan and Peter Borwein, together with Simon Plouffe, also developed this series for pi:
infinity __________ \ / \ \ 1 | 4 2 1 1 | > ----- * | --------------- - --------------- - --------------- - --------------- | / i | ((8 * i) + 1) ((8 * i) + 4) ((8 * i) + 5) ((8 * i) + 6) | /_________ 16 \ / i = 0
For i=2, for example, the term would be 1/256 * (4/17 - 2/20 - 1/21 - 1/22).
Now, neither 4/17 nor 1/21 nor 1/22 are fractions which have a terminating representation in hexadecimal notation any more than they would in decimal notation. (For that matter, 2/20, or 1/10, terminates in decimal notation, but it doesn't terminate either in hexadecimal notation.)
However, it is still possible to use this series in an efficient procedure for calculating hexadecimal digits of pi at an arbitrary position without needing to also calculate the digits which come before them, even if how to do this is not trivial.
An improved formula of this type was subsequently developed by Fabrice Bellard:
infinity
__________
\ i / \
1 \ (-1) | 256 64 4 4 1 32 1 |
---- * > ------- * | ---------------- - ---------------- - ---------------- - ---------------- + ---------------- - --------------- - --------------- |
64 / i | ((10 * i) + 1) ((10 * i) + 3) ((10 * i) + 5) ((10 * i) + 7) ((10 * i) + 9) ((4 * i) + 1) ((4 * i) + 3) |
/_________ 1024 \ /
i = 0
Initially, when the first of these series was discovered, there was optimism that a similar formula for calculating high-order decimal digits of pi directly might also be found.
Later, however, a proof was found that a formula of this particular type could not exist for bases other than powers of two because these formulas are related to arctangent relations for pi, such as the identity of Machin noted above, which do not exist in a suitable form for other bases.
Still later, though, a formula of a different type was found that allowed direct calculation of high-order decimal digits of pi. The first such one was found by Simon Plouffe; however, it was quite slow, as the time it would take is proportional to the cube of the position of the digit to be found.
Improved algorithms for high-order decimal digits of pi have since been found, but they are still too slow to be competitive with calculating the entire number. However, they are still of theoretical importance, as it might be possible to gain insights from them for a proof, one way or another, addressing the still unsolved question of whether the digits of pi behave statistically like a sequence of random digits: whether or not pi is normal.
As an alternative way of calculating pi, it occured to me that if there was a high-speed arithmetic-geometric mean algorithm for calculating the arctangent, one could use a Machin-type arctangent relation in connection with that, instead of with the Gregory series.
The first such method I found described in an early paper on the subject of efficient algorithms for the elementary functions required the use of an algorithm for calculating the logarithm that required the value of pi to the full length of the numbers being worked with, but I later found a web page with one without this limitation:
a(0) = sqrt(1 + x^2) b(0) = 1 a(n+1) = (1/2) * (a(n)+b(n)) b(n+1) = sqrt( a(n+1) * b(n) )
with the arctangent of x being approximated by x/(a(N) * sqrt(1+x*x)), where N is the number of iterations carried out, originally given in Numerical Methods that Work by Forman S. Acton, as cited on the Wolfram Research web site.
Machin-like identies have been found that converge even more quickly than the ones given above as having been used in practice. One that I saw which would converge particularly quickly, even using the Gregory series, was this one:
atn(1) = 183*atn(1/239) + 32*atn(1/1023) - 68*atn(1/5832) + 12*atn(1/113021) - 100*atn(1/6826318) - 12*atn(1/33366019650) + 12*atn(1/43599522992503626068)
so there is an arctangent identity with atn(1/239) as the slowest-converging term; this identity was derived by Hwang Chien-Lih in 1997, but he has since derived even better ones, the best one I have seen anywhere having been found by him in 2004:
atn(1) = 36462*atn(1/390112) + 135908*atn(1/485298) + 274509*atn(1/683982) - 39581*atn(1/1984933) + 178477*atn(1/2478328) - 114569*atn(1/3449051) - 146571*atn(1/18975991) + 61914*atn(1/22709274) - 69044*atn(1/24208144) - 89431*atn(1/201229582) - 43938*atn(1/2189376182)
at least, that was the best one I had seen anywhere, when I came across it on Wikipedia, but then I found his web site on the subject, which includes even better ones, such as:
atn(1) = 20435891*atn(1/28841295) + 6458959*atn(1/133311327) + 10571216*atn(1/152087733) - 190529*atn(1/159358932) + 5127580*atn(1/213495433) + 7798670*atn(1/227661182) - 3154610*atn(1/278263393) - 14603096*atn(1/284862638) - 5959396*atn(1/355671793) - 10585611*atn(1/727507932) - 4139726*atn(1/934981432) + 1560722*atn(1/15234751332) - 2675312*atn(1/106334643058) + 6769449*atn(1/138873731225) + 2229180*atn(1/293153860797) - 2967682*atn(1/169838669284032)
Since the successive terms in Gregory's series for the arctangent of x involve x, x^3, x^5, and so on, being multiplied by x^2 each time, having x as one over an eight-digit number means that each step involves multiplying by one over a sixteen digit number, so, although there are more series to sum, this is enough to make Gregory's series comparable to Chudnovsky's series, if still not necessarily quite as fast.
Also, incidentally, since
atn(1) = 183*atn(1/239) + 32*atn(1/1023) - 68*atn(1/5832) + 12*atn(1/113021) - 100*atn(1/6826318) - 12*atn(1/33366019650) + 12*atn(1/43599522992503626068)
and
atn(1) = 4*atn(1/5) - atn(1/239)
we can calculate atn(1/5) as an intermediate result:
atn(1/5) = 46*atn(1/239) + 8*atn(1/1023) - 17*atn(1/5832) + 3*atn(1/113021) - 25*atn(1/6826318) - 3*atn(1/33366019650) + 3*atn(1/43599522992503626068)
which is not surprising, as one expects that these formulas are obtained by repeated application of the tangent addition formula.
Similarly, since
atn(1) = 12*atn(1/18) + 8*atn(1/57) - 5*atn(1/239)
and
atn(1) = 4*atn(1/5) - atn(1/239)
we can also say:
atn(1/5) = 3*atn(1/18) + 2*atn(1/57) - atn(1/239)
Thanks to another identity by Störmer,
atn(1) = 44*atn(1/57) + 7*atn(1/239) - 12*atn(1/682) + 24*atn(1/12943)
knowing also that
atn(1) = 12*atn(1/18) + 8*atn(1/57) - 5*atn(1/239)
we can deduce that
atn(1/18) = 3*atn(1/57) + atn(1/239) - atn(1/682) + 2*atn(1/12943)
and so we have component relations that can be used to trace a line of descent for that identity from Machin's original formula.
Hunting around, I've found another related identity on the web:
atn(1) = 88*atn(1/172) + 51*atn(1/239) + 32*atn(1/682) + 44*atn(1/5357) + 68*atn(1/12943)
so now we can find an expression for atn(1/57) in terms of arctangents of smaller quantities.
However, there's another formula that starts with atn(1/239), unlike the one I first encountered, that is related (it may be due to Jörg Arndt):
atn(1) = 183*atn(1/239) + 44*atn(1/515) - 56*atn(1/682) + 88*atn(1/6050) + 24*atn(1/12943) - 88*atn(6826318)
With that and
atn(1) = 44*atn(1/57) + 7*atn(1/239) - 12*atn(1/682) + 24*atn(1/12943)
we can deduce
atn(1/57) = 4*atn(1/239) + atn(1/515) - atn(1/682) + 2*atn(1/6050) - 2*atn(6826318)
Thus, we now have a series of formulas starting with Machin's original formula, and ending with one the slowest-converging term of which is atn(1/239), where we can follow how the slowest-converging term is replaced with faster-converging ones every step of the way:
atn(1) = 4*atn(1/5) - atn(1/239)
+ 4 * 0 = - atn(1/5) + 3*atn(1/18) + 2*atn(1/57) - atn(1/239)
-----------------------------------------------------------------------
atn(1) = 12*atn(1/18) + 8*atn(1/57) - 5*atn(1/239)
+ 12 * 0 = - atn(1/18) + 3*atn(1/57) + atn(1/239) - atn(1/682) + 2*atn(1/12943)
-------------------------------------------------------------------------------------------------------------------------------------------
atn(1) = 44*atn(1/57) + 7*atn(1/239) - 12*atn(1/682) + 24*atn(1/12943)
+ 44 * 0 = - atn(1/57) + 4*atn(1/239) + atn(1/515) - atn(1/682) + 2*atn(1/6050) - 2*atn(6826318)
-------------------------------------------------------------------------------------------------------------------------------------------------------------
atn(1) = 183*atn(1/239) + 44*atn(1/515) - 56*atn(1/682) + 88*atn(1/6050) + 24*atn(1/12943) - 88*atn(6826318)
Yet another possible arctangent relation, closely related to the one examined here, is:
atn(1) = 183*atn(1/239) - 12*atn(1/682) + 44*atn(1/1240) + 24*atn(1/12943) - 44*atn(1/2485057) - 88*atn(6826318)
which can be considered slightly improved, since now when atn(1/239) is removed at the next step, the slowest-converging term would be atn(1/682) instead of atn(1/515). This relation was developed by Michael Roby Westerfield, a collaborator with Hwang Chien-Lih.
Here is a record of the notable errors in the computation of pi:
The value of pi given by de Lagny to 126 places in 1719 had a 7 instead of an 8 in the 113th place, giving 32723 instead of 32823 in positions 111 to 115.
The value of pi given by Georg Freyherrn von Vega (or Jurij Vega) in 1789 was:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 44767 21386 11733 138
in 1794, he corrected his error. He is best known for having calculated a set of 10-figure logarithm tables which were of inestimable value to generations of mathematicians and scientists.
The value of pi given by William Rutherford in 1851 was:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48473 78139 20386 33830 21574 73996 00825 93125 91294 01832 80651 744
This value was first corrected by Zacharias Dase; later, William Rutherford calculated pi to more places, without error.
The 707 digits computed by William Shanks, of which the first 527 were correct, which appeared in countless sources, sometimes with misprints of various types, from 1873 onwards, were:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 72458 70066 06315 58817 48815 20920 96282 92540 91715 36436 78925 90360 01133 05305 48820 46652 13841 46951 94151 16094 33057 27036 57595 91953 09218 61173 81932 61179 31051 18548 07446 23799 62749 56735 18857 52724 89122 79381 83011 94912 98336 73362 44065 66430 86021 39501 60924 48077 23094 36285 53096 62027 55693 97986 95022 24749 96206 07497 03041 23668 86199 51100 89202 38377 02131 41694 11902 98858 25446 81639 79990 46597 00081 70029 63123 77381 34208 41307 91451 18398 05709 85
In the December 18, 1873 issue of the Proceedings of the Royal Society of London, in which typographical errors in the original publication of Shanks' value were noted, these digits appeared, except that the 679th digit was a 7 instead of a 1, giving 77387 for the 675th through 679 digits.
That digit, not among the typographical errors noted, however, appeared as a 1 in the original publication of Shanks' value in the May 15, 1873 issue of that journal, and thus the most reliable reproductions of Shanks' value give 1 as the digit in that position.
William Shanks also gave the values of the arctangents of 1/5 and of 1/239 which he calculated in order to obtain pi, thus helping those who would seek to locate the error in his calculatiion.
His value of the arctangent of 1/5, with the digits in error shown in bold, was:
0.19739 55598 49880 75837 00497 65194 79029 34475 85103 78785 21015 17688 94024 10339 69978 24378 57326 97828 03728 80441 12628 11807 36913 60104 45647 98867 94239 35574 75654 95216 30327 00522 10747 00156 45015 56006 12861 85526 63325 73186 92806 64389 68061 89528 40582 59311 24251 61329 73139 93397 11323 35378 21796 08417 66483 10525 47303 96657 25650 48887 81553 09384 29057 93116 95934 19285 18063 64919 69751 94017 08560 94952 73686 73738 50840 08123 67856 14800 93298 22514 02324 66755 49211 02670 45743 78815 47483 90799 78985 02007 52236 96837 96139 22783 54193 25572 23284 13846 47744 13529 09705 46512 24383 02697 56051 83776 17781 64242 33783 03370 18192 64880 28277 68611 91509 85606 75901 21359 85563 63034 32100 56649 97826 76360 88711 52327 56610 84900 93773 38023 19504 70687 65729 38513 59243 19759 37947 36057 50636 20935 07853 2833
which value includes a correction to the 75th digit, which was originally printed in error as a 7 instead of an 8 (69977 instead of 69978).
and his value of the arctangent of 1/239 was:
0.00418 40760 02074 72386 45382 14959 28545 27410 48065 30763 19508 27019 61288 71817 78341 42289 32737 82605 81362 29094 54975 45066 64448 63756 05245 83947 89311 86505 89221 28833 09280 08462 71962 33077 33759 47634 60331 84734 14570 33198 60154 54814 80599 24498 30211 46039 12539 49527 60779 68815 58881 27339 78533 46518 04574 25481 35867 46447 51979 10232 83097 70020 64652 82763 46532 96910 48183 86543 56078 91959 14512 32220 94463 68627 66155 20831 67964 26465 74655 11032 51034 35262 82445 12693 55670 49968 44452 47904 33177 28393 07086 31401 93869 51950 37058 64107 70855 85540 45223 55388 14237 67708 36515 69182 52702 00229 30895 44950 04358 54409 34496 44014 24187 24950 92283 86239 54553 33565 16494 21220 06852 38821 94006 45849 29313 23886 73467 64889 18731 81682 83021 21101 37897 11546 96191 84692 18237 33903 04682 04140 79985 6684
In 1853, he had Contributions to Mathematics, Consisting Chiefly of the Rectification of the Circle to 607 Places of Decimals published. It included arctan(1/5) and arctan(1/239) to 609 places, which both were largely in agreement with the later 707-place values, that of arctan(1/5) to 601 of its 609 places, but that of arctan(1/239) agreed in its entirety.
Since his value of arctan(1/5) was only correct to 529 places, that portion of his error in the 707-digit value had already happened in that calculation; the value of arctan(1/5), used in the 707-digit calculation of pi was correct to 591 places, so that part of the error had also already happened.
The book also included the individual terms of the arctangent series that he calculated, but these were only given to 527 places, and so they do not give an opportunity to check the part of his calculation that was in error. An offer was made in the text to provide supplementary sheets giving the details of the latter portion of the calculation, but as this offer appears not to have been taken up, the error in the 607-digit calculation of pi, also present in the 707-digit calculation of pi, was not noted until much later, and so there was an opportunity that was missed.
The value of pi to 808 digits as first given by D. F. Ferguson in March, 1947, had several individual digits in error starting from the 723rd digit, but then continued on with digits that were correct.
The correct value of pi to 810 digits is:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 72458 70066 06315 58817 48815 20920 96282 92540 91715 36436 78925 90360 01133 05305 48820 46652 13841 46951 94151 16094 33057 27036 57595 91953 09218 61173 81932 61179 31051 18548 07446 23799 62749 56735 18857 52724 89122 79381 83011 94912 98336 73362 44065 66430 86021 39494 63952 24737 19070 21798 60943 70277 05392 17176 29317 67523 84674 81846 76694 05132 00056 81271 45263 56082 77857 71342 15778 96091 73637 17872 14684 40901 22495 34301 46549 58537 10507 92279 68925 89235 42019 95611 21290 21960 86403 44181 59813 62977 47713 09960 51870 72113 49999 99837 29780 49951 05973 17328 16096 31859 50244 59455
and that initially given by D. F. Ferguson with the incorrect digits shown in bold and underlined as well, to make these intermittent incorrect digits easier to pick out, is:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 72458 70066 06315 58817 48815 20920 96282 92540 91715 36436 78925 90360 01133 05305 48820 46652 13841 46951 94151 16094 33057 27036 57595 91953 09218 61173 81932 61179 31051 18548 07446 23799 62749 56735 18857 52724 89122 79381 83011 94912 98336 73362 44065 66430 86021 39494 63952 24737 19070 21798 60943 70277 05392 17176 29317 67523 84674 81846 76694 05132 00056 81271 45263 56082 77857 71342 15778 96091 73637 17872 14684 40901 22495 34301 46549 58537 10507 92279 68925 89235 42019 95611 21290 21960 86355 44191 19716 02977 46113 09960 51870 72113 49999 99837 29780 49951 05973 17328 16096 31867 50244 59455
The last two digits of these 810 digits were in parentheses, indicating that their value was uncertain; these appeared in March 1947, and he corrected himself by September 1947.
I've begun work on expanding this page and dividing it into several pages; I had abandoned the project, because it seemed that an initial index page would not be of interest, but as there had been some added material, I've decided to quickly finish off an initial version of the page in its divided form, so as to make the added material on the second page, First Steps in Calculating Pi, immediately available; over time, I may reduce the amount of duplication on the first page and add material to the other pages.