The number of ways in which n objects may be arranged is known in mathematics as n factorial, which is written as n! .
A short table of the first few factorials follows:
0 1 1 1 2 2 3 6 4 24 5 120 6 720 7 5040 8 40320 9 362880 10 3628800 11 39916800
For positive integer arguments, Gamma(n) is equal to (n-1)! and so Gamma(1) and Gamma(2) are both equal to 1, Gamma (3) equals 2, and so on.
For values of z with real part greater than zero, the Gamma function is defined by the equation
_
/ \ infinity
| z-1 -u
Gamma(z) = | u e , du
|
\_/ 0
There is also an important infinite product for the Gamma function, due to Euler, which is valid for all finite z:
infinity / z \
____________ | / \ - --- |
1 gamma z | | | | z | n |
---------- = z e | | | | 1 + --- | e |
Gamma(z) | | | | n | |
--- --- | \ / |
n = 1 \ /
The "gamma" that appears on the right side of the equals sign in the equation above isn't the Gamma function, it's Euler's constant, about 0.57221566... .
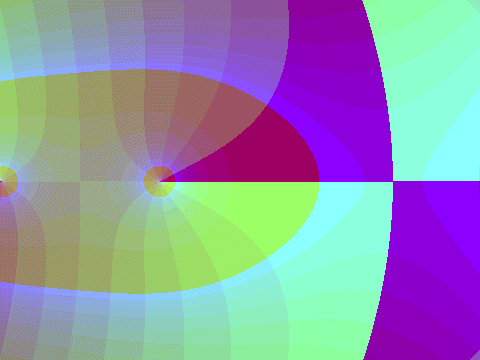
From another page, here's an image of what the Gamma function looks like over the complex plane:

One important formula giving a property of the Gamma function is Euler's reflection formula for the Gamma function:
pi
Gamma(z) * Gamma(1-z) = ---------------
sin( pi * z )
This formula is not valid for the points where the function is not defined because it goes to infinity, at zero and at the negative integers.
As it happens, the Gamma function appears in the reflection formula for the Riemann zeta function, a very important mathematical function because it relates to the prime numbers, thus allowing the tools of mathematical analysis to be brought to bear against number theory problems involving the prime numbers.
z (z - 1) pi * z
zeta( z ) = 2 * pi * sin( -------- ) *Gamma( 1 - z ) * zeta( 1 - z )
2
This equation is known as Riemann's functional equation for the Riemann zeta function.
The mathematician G. H. Hardy is known for writing A Mathematician's Apology in which he argues for the value of pure mathematics. He is perhaps even better known for having introduced Srinivasa Ramanujan to the world.
But Ramanujan would not have contacted him if he hadn't been a renowned mathematician in his own right. And one of his discoveries was a proof that the Riemann zeta function had an infinite number of zeroes of the form 1/2 + yi. This was important, as it is related to the famous Riemann hypothesis that all the zeroes of the Riemann zeta function are either trivial zeroes on the real line, or zeroes of the form 1/2 + yi.
Another proof has established that all the non-trivial zeroes of the Riemann zeta function are at least of the form x + yi for 0 < x < 1. And it follows very simply from the reflection formula for the Riemann zeta function shown above that if there are zeroes of that function which are counterexamples to the Riemann hypothesis, then they will be in symmetrical pairs on the two sides of the x = 1/2 line.
Hardy's proof that, whether or not the Riemann hypothesis is true, at least an infinite number of the zeroes of the Riemann zeta function are of the form which that hypothesis claims that all the non-trivial zeroes should be is also based on that reflection formula, but in a more complicated way.
Just as I generated a diagram of the Gamma function on the complex plane that was shown above, I also generated one for the Riemann zeta function, and here it is:
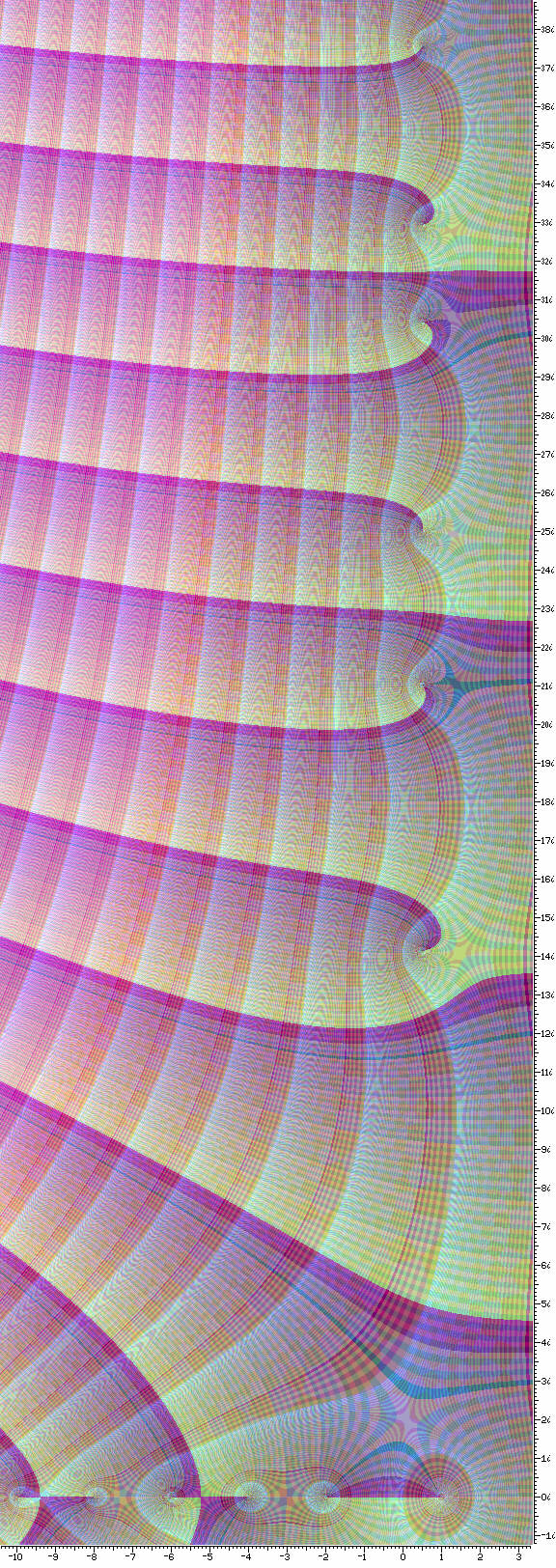
In this diagram are visible the simple pole of the Riemann zeta function at 1 on the real axis, and the trivial zeroes of the Riemann zeta function at -2, -4, -8, and -10 on the real axis. Yes, it also has trivial zeroes for every other even negative number as well.
And the first six non-trivial zeroes of the Riemann zeta function are also visible on the diagram, the ones at
0.5 + 14.13472... i 0.5 + 21.02204... i 0.5 + 25.01085... i 0.5 + 30.42487... i 0.5 + 32.93506... i 0.5 + 37.58617... i