And now we will conclude with a variety of other older machines, and then proceed to somewhat more modern ones.
Since we just looked at the Burtmeier Pony, one version of which had pictures of dice on its reels instead of fruit symbols, it may be appropriate now to look at some specialized forms of slot machine that attempted to more closely simulate dice play, specifically the game of Craps.
A slot machine very highly prized by collectors is the Buckley Bones. This machine has two reels, but instead of the reels having paper strips on which symbols are printed, the reels have compartments, each containing two dice. So as the reels spin to present a compartment with a pair of dice within it, the machine presents an illusion of throwing dice.


The Buckley Bones and the Bally Reliance, except for their branding and styling, are essentially identical. The Bally Reliance is pictured at right, and the Buckley Bones at left. The Bally Reliance first became available in early 1936; the Buckley Bones appears to have become available only in 1937, and apparently the Reliance was the original machine, with the Bones being the same mechanism but with a new cover.
The operation of these machines follows the course of the game of craps.
After inserting a coin, pulling the lever spins the first reel only. If a compartment shows with 2, 3, or 12, that is the end of the player's turn, and the player loses.
If a compartment shows with 7 or 11, the player wins 2 coins.
Otherwise, without inserting another coin, the player may pull the lever again, this time spinning the second reel. If a 7 turns up, the player loses. If the number shown on the first reel is matched, the player wins; but instead of winning even money, as in craps, the payoff varies depending on wht the pont is.
If the player's point is 6 or 8, winning pays even money. If the point is 4, 5, 9, or 10, however, a winning player is paid 8 for 1 (or 7 to 1).
Also, if one won by an initial 7 or 11 four times in a row, one won a Gold Award, presumably a jackpot-sized prize.
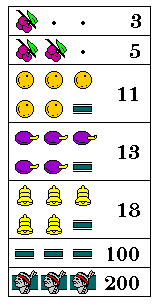
Each reel on the Reliance or the Bones had 13 compartments.
The contents of the left reel were:
7 1 11 1 2 1 3 - 12 1 4 1 5 1 6 2 8 3 9 1 10 1
So initially the player had a 2/13 chance of losing and a 2/13 chance of winning. The chance of a Gold Award was 16/28561.
The contents of the right reel were:
7 7 4 1 5 1 6 1 8 1 9 1 10 1
If a point other than the player's point comes up, the player can pull the lever again without paying another coin for another spin of the second reel.
Thus we can calculate the machine's payout percentage: out of 104 coins played, 13 times 8, the player will recieve:
2/13 * 2 coins 32 (out of 104)
4/13 * 1/8 * 8 coins 32
2/13 * 1/8 * 2 coins 4
16/28561 * 100 coins 4.826
__
72.826 out of 104
for a payout percentage of 70.025%, as the Gold Award was worth 100 coins.
The Mills Novelty Company made a machine of their own which competed with the Reliance and the Bones which was even more elaborate, the Mills Dice. It may even have predated the Reliance and the Bones, for that matter, as it seems to have been advertised a month earlier than they were.

Before either the Mills Dice and the Reliance and the Bones, Western Equipment and Supply had a very successful machine, with an automatic payout, that also was designed to give the appearance of dice being thrown, the Mysterious Eye, pictured at left. It was simpler than even the Reliance, one spin simply led to two pairs of dice becoming immediately visible - and the winning combinations were not closely patterned after those of the game of craps either. It was popular at the time, setting sales records in 1935, so it is would not have been surprising that it inspired attempts to improve on it.
However, I learned that Mills had applied for a patent on the Mills Dice machine fairly early in its development process, so it was actually that patent that created a buzz in the amusement machine industry and led to the development of both the Reliance and the Mysterious Eye.
The Mysterious Eye is described in U. S. Patent 2,135,182. It turns out that it managed to provide automatic payout while actually throwing dice. This was managed by using dice that were not perfectly cubical, but which instead had at least one pair of faces slightly closer together than the others. Thus, after the dice were thrown, the baseplate moved up to hold the dice against the glass faceplate, and partial information about how the dice were facing could be obtained from where the base plate moved.
Assuming the alteration in the shape of the dice did not materially affect how they rolled:
The machine awarded "10 points" for any combination of 1 and 6 in the first two compartments, which would have a 1/9 chance of occurring.
But it would award "30 points" instead if 1 or 6 also came up in the third compartment.
If 1, 3, 4, or 6 came up in the fourth compartment when either of the previous winning combinations was present, "30 points" would also be awarded.
So on the first three dice, 1 and 6 were the faces that were closer together, while on the fourth die, 2 and 5 were closer together.
The chance of only winning 10 points would be 1/9 times (2/3 times 1/3), or 2/81, and the chance of winning 30 points would be 7/81, if I understand the payout schedule correctly.
A 10 point win returned two nickels, so assuming a 30 point win returns six nickels, and one pays a nickel to play, the machine would return 46 nickels for every 81 nickels played, about 56.79%, for a house advantage of 43.21%.

On the Mills Dice, pictured at right, there were three openings through which a coin could be inserted for three possible bets.
One could bet on 11, for a payout of 16 coins if one won.
One could bet on the field, for a payout of 2 coins if either 2, 5, 9, 10, 11, or 12 came up; originally, I thought it was if 2, 3, 5, 8, 10, 11, or 12 came up, as that was what was shown on an early advertisement for the machine, but I have since learned the correct set of numbers for the field, first from a forum post, and then I checked a video of an actual machine to confirm this. The larger set of winning numbers shown in the advertisement would have had an exact 50% chance of coming up, which would mean that bet would make no profit.
One could play a pass/come bet, which followed the normal rules of the game of Craps; 7 or 11 won, 2, 3, or 12 lost, on the first throw, and subsequently one won with one's point, or lost with a 7.
The machine presented a more elaborate illusion of dice being thrown than the Reliance and Bones.
Two dice were ejected, from a ring of thirty dice, into a round area. The area was divided into two chambers, one for each die. In preparation for a subsequent throw, each die would be returned from its chamber into the part of the ring from which it came. The dice had no opportunity to tumble; the numbers on the die were determined by the part of the ring of dice from which they came, not by tumbling when thrown.
All throws of the dice, the first one and subsequent ones, came from the same thirty possibilities, thus making this machine different from the Reliance and Bones, which had one reel for the come-out roll and one reel for subsequent rolls.
The thirty possible rolls of the dice were distributed as follows:
7 5 11 1 2 2 3 4 12 2 4 2 5 2 6 4 8 4 9 2 10 2
A throw of 7 comes up 5 times out of 30, one-sixth of the time, exactly as with real dice. Other possibilities, however, have changed.
11 comes up one time out of 30, but only pays 16 coins, so that bet only returns 53.33% of what the player wagers.
The winning Field numbers are 2, 5, 9, 10, 11, or 12, and those six numbers cover 11 possibilities, returning 22 coins out of 30, or 73.333...%. Had the numbers I had seen in the early advertisement been the winners instead, 2, 3, 5, 8, 10, 11, or 12, they would cover 15 out of 30 possibilities, making that bet fair.
The bet that is presumably the most popular would be the one involving most of the machine's complexity, the one that simulates the game of craps.
The odds break down like this:
6/30 chance of winning on the first roll (7,11) 756 coins
8/30 chance of losing on the first roll (2, 3, 12)
8/30 chance of having a 2/7 chance to win (4, 5, 9, 10) 288 coins
8/30 chance of having a 4/9 chance to win (6, 8) 448 coins
----
1492
so out of 63 * 30 coins played, that is, 1,890 coins, the player would recieve 1.492 coins in return, for a payout percentage of 78.94%, and thus that bet yielded a house advantage of 21.06%.
When Bally introuduced the Reliance at the 1936 Coin Machine Show, this introduction was accompanied by a show, "Dance of the Dice", presented by The Two Zephyrs, a comedy and dance act.
The Two Zephyrs performed with Duke Ellington over a period of several years, so they were apparently an act of some significance.
One of the Two Zephyrs, who I only know of as "Big Zeph", passed away in 1940, and Melvin Edward White, known as "Slappy" White, replaced him. The remaining partner, "Little Zeph", was Clarence Schelle.
Melvin White later left the Two Zephyrs; another comedy act, Canfield and Lewis, consisting of James "Spizzy" Canfield and Willie Lewis broke up, and White joined with Lewis to form Lewis and White. Then, in 1947, he moved on again, to team up with Redd Foxx.
Of course, we remember Redd Foxx from the television show "Sanford and Son", on which Melvin Lewis made a guest appearance; before, he had a... salty... comedy routine, and some phonograph records of it exist as well.
Meanwhile, the Two Zephyrs continued to exist, performing with Duke Ellington at least as late as 1950 (and as early as 1937, as well, from accounts I have seen). So the act did continue after Melvin Lewis, replacing him.
However, while Melvin Lewis is remembered due to other successes in his career, so far I have not been able to find out who he replaced, or who he was replaced by, in the few accounts of the group I have been able to find online.
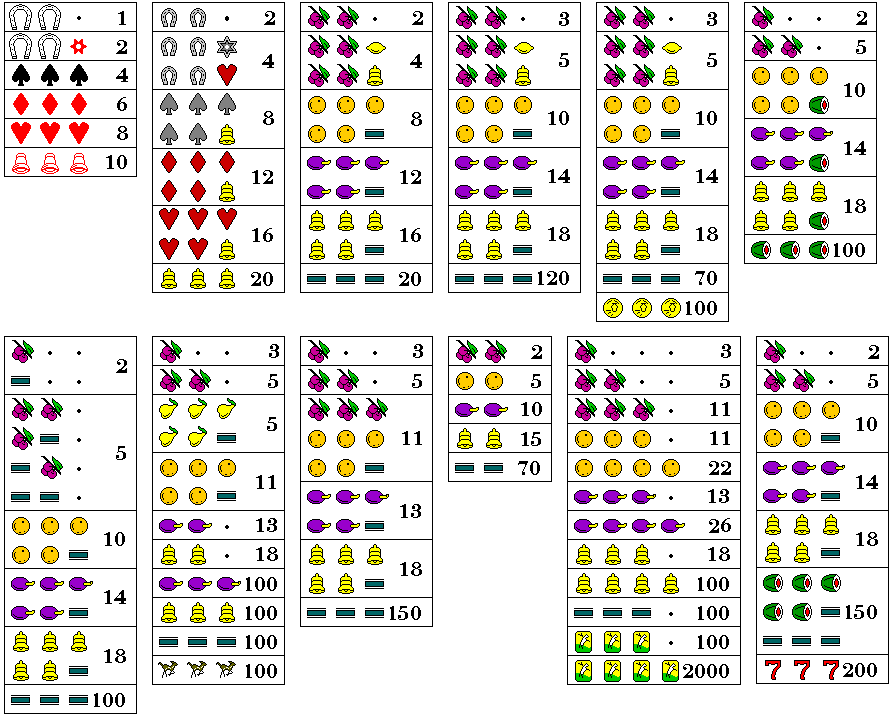
Repeating the earlier image of slot machine payouts through the years for ease of reference:

The fifth arrangement on the second row is that of another machine made by Jennings. The payout for four plums is depicted as 26; on the original Jennings Buckaroo, it was 22 in order to simplify the payout mechanism slightly, but on the Jennings Golden Nugget, it was made 26 to be double that for three plums. The Jennings Buckaroo was the first four-reel machine introduced after World War II. The most common date I have seen given for it is 1955, but some sources say it came out in 1958, and one source says that Jennings at least began producing them in 1954. This is an important date because in advertising for Jennings slot machines up to 1950, when slot machines were still being widely sold, no evidence of cherries on the third reel has turned up; since the payout structure of the four-reel Jennings Buckaroo includes cherries on the third reel, if not the fourth, it seems likely that their three-reel machines with cherries on the third reel either became available at the same time, or preceded it.
One arrangement of symbols on the reels for the Jennings Buckaroo (that of the V12-117 reel strips) is the following:
Cherry 2 6 3 - Orange 6 2 4 10 Plum 4 1 10 6 Bell 3 7 1 3 Bar 4 3 1 - Buckaroo 1 1 1 1
which leads to payouts (from 160,000 coins instead of 8,000) as follows:
Reel Combinations Value Amount
1 2 3 4 Paid
%... 3 2 * 14 * 20 * 20 = 11,200 * 3 = 33,600
%%.. 5 2 * 6 * 17 * 20 = 4,080 * 5 = 20,400
%%%. 11 2 * 6 * 3 * 20 = 720 * 11 = 7,920
OOO. 11 6 * 2 * 4 * 10 = 480 * 11 = 5,280
OOOO 22 6 * 2 * 4 * 10 = 480 * 22 = 10,560
@@@. 13 4 * 1 * 10 * 14 = 560 * 13 = 7,280
@@@@ 26 4 * 1 * 10 * 6 = 240 * 26 = 6,240
AAA. 18 3 * 7 * 1 * 17 = 357 * 18 = 6,426
AAAA 100 3 * 7 * 1 * 3 = 63 * 100 = 6,300
===. 100 4 * 3 * 1 * 20 = 240 * 100 = 24,000
BBB. 100 1 * 1 * 1 * 19 = 19 * 100 = 1,900
BBBB 2000 1 * 1 * 1 * 1 = 1 * 2,000 = 2,000
-------
131,906
which gives a payout percentage of just over 82.44%.
The V12-112 reel strips give another arrangement of symbols on the reels for the Jennings Buckaroo, with slight modifications to the first two reels, and a major transformation of the fourth reel. However, there are no oranges on the fourth reel in that set as pictured in my source; if I change one of the plums on that reel to an orange, I would get:
Cherry 2 7 3 - Orange 7 2 4 1 Plum 5 1 10 6 Bell 3 8 1 3 Bar 2 1 1 - Buckaroo 1 1 1 10
and that would work out to the following:
Reel Combinations Value Amount
1 2 3 4 Paid
%... 3 2 * 13 * 20 * 20 = 10,400 * 3 = 31,200
%%.. 5 2 * 7 * 17 * 20 = 4,760 * 5 = 23,800
%%%. 11 2 * 7 * 3 * 20 = 840 * 11 = 9,240
OOO. 11 7 * 2 * 4 * 19 = 1,064 * 11 = 11,704
OOOO 22 7 * 2 * 4 * 1 = 56 * 22 = 10,560
@@@. 13 5 * 1 * 10 * 14 = 700 * 13 = 9,100
@@@@ 26 5 * 1 * 10 * 6 = 300 * 26 = 7,800
AAA. 18 3 * 8 * 1 * 17 = 408 * 18 = 7,344
AAAA 100 3 * 8 * 1 * 3 = 72 * 100 = 7,200
===. 100 2 * 1 * 1 * 20 = 40 * 100 = 4,000
BBB. 100 1 * 1 * 1 * 10 = 10 * 100 = 1,000
BBBB 2000 1 * 1 * 1 * 10 = 10 * 2,000 = 20,000
-------
142,948
which gives a payout percentage of just over 89.34%, so changing the plum to an orange did not create an unprofitable, and hence impossible, set of reel strips.
The payouts for the Jennings Buckaroo are also reproduced again in the second column of the image below:

The first four-reel conventional slot machine (five-reel machines with playing card symbols, and without automatic payout, predated the conventional slot machine) was one by Caille from 1930, well before the war, illustrated at right. Instead of extending the machine by adding another reel on the right, the Caille Grand Prize, a four-reel model of the Caille Superior, had one extra reel on the left; the only symbol on it was a lemon, the other positions being blank; thus, that lemon was required for a special larger jackpot, while the prizes for the combinations on the other three reels remained unaffected.
That resulted in a payout schedule like that illustrated as the first arrangement in the image above however, one could only win the grand prize if the symbols lined up also had the digits 1, 2, 3, and 4 overprinted on them, and this was not true of all the lemons on the second reel, all the bells on the third reel, or all the lemons on the fourth reel, so winning the prize was more unlikely than just having all the appropriate symbols lined up would be.
One set of reel strips for this machine had the following distribution of symbols:
Blank 16 - - - Lemon (U) - 1 - 2 Lemon (N) 4 2 - 2 Cherry - 5 5 - Orange - 3 5 5 Plum - 3 3 5 Bell (U) - 4 3 3 Bell (N) - - 2 - Bar - 2 2 3
Thus, out of 160,000 pulls, the four-reel jackpot would come up 32 times, or once out of 5,000 pulls. This prize was typically equivalent to 100 coins, so it was neither particularly larger nor particularly more unlikely, than a jackpot could be from a conventional three-reel machine.
Although the machine had automatic payout for the other prizes, the four-reel jackpot was awarded by the operator.
The five-reel machines with playing cards that preceded Charles Fey's original Liberty Bell slot machine were classed as trade stimulators in the terminology used by antique collectors, as one had to put a coin in to pull the lever and spin the wheels, but then the merchant would have to look at the combination displayed to pay out any prize manually. The "New Deal" trade stimulator by Pierce had five reels, but one could change the front of the machine to display only three or four of them. So it could have five reels with playing cards, with prizes awarded based on poker hands, it could have three reels with the Mills fruit symbols, and payouts like those of a slot machine, or it could have four reels, where the three reels in the middle had Mills fruit symbols, but the fourth reel, either on the left or the right, showed a payout amount, which would be awarded if any three matching fruit symbols came up.
Another more conventional four-reel slot machine, in addition to the one made by Jennings, was made by Pace, as a variation of the Pace Comet Deluxe, and its payouts are illustrated in the third column of the illustration above.
The fourth column shows a set of payouts used by Mills, when, somewhat late in the era of mechanical slot machines, it presented its own take on the four-reel slot machine in a Hi-Top body.
I've also seen images of four-reel slot machines apparently by Mills with other payout schedules: one with a basically identical payout schedule, except that four oranges only pay 14 and four plums only pay 18, and one where in addition to substituting for oranges, plums, and bells on the third reel, the bar can substitute for oranges, plums, and bells on the fourth reel as well.
Instead of the melon, shown here as an additional jackpot symbol, the machine as manufactured used an owl, the Mills trademark, in a circle, but that symbol was often replaced by a symbol representing the casino using the machine.
Like the Pace four-reel machine, four oranges and four plums give the same prize, and like both the Jennings Buckaroo and the Pace four-reel machine, four bells are a jackpot.
But in some ways, this machine's payout schedule illustrates that Mills remained steeped in classic slot machine tradition. Cherries are still found only on the first two reels. The bar substitutes for an orange, plum, or bell on the third reel, where it had always done so on three-reel machines.
More recently, slot machines had been designed to have 22, 23, or 25 positions per reel, and currently electronic machines are used in casinos that simulate a slot machine with perhaps 128 positions on each reel, and so it's hardly necessary to add a fourth reel if one wishes to have a large jackpot that would have to also be very infrequent.
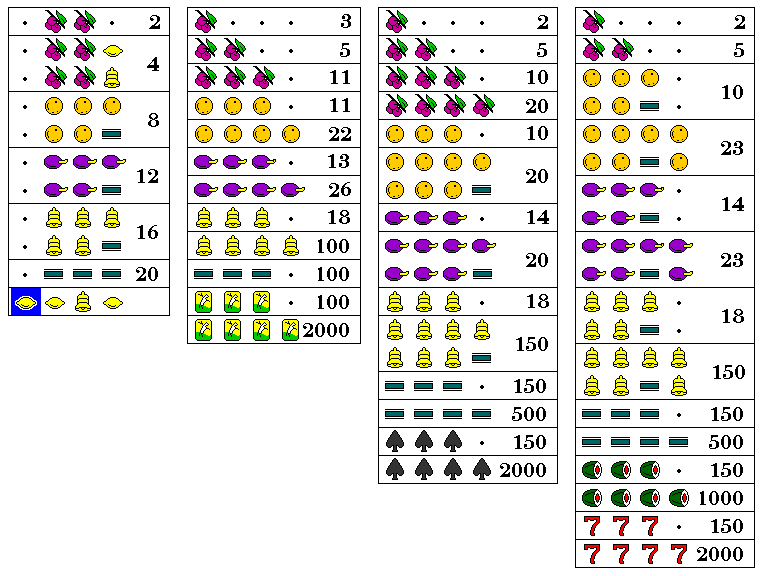
While the fruit symbols introduced on the Mills Operator's Bell quickly became the standard, slot machines were made which instead had patriotic symbols on the reels, or symbols associated with baseball or other sports.
One company, Caille, initially attempted to use fruit symbols, as made popular by the Mills machines, without copying their set of fruit symbols exactly.

The first set of payouts in this illustration show the appearance of the symbols in the Caille Operator's Bell. In the Caille Liberty Bell, which used the same fruit symbols, the letters G, U, and M overlaid the fruit symbols as in the first Mills machines with fruit symbols, where the spearmint leaf was present instead of the cherry. However, while the reel strips of those Mills machines represented the letters G, U, and M in a variety of ways, for example drawing square letters on the Bell, building letters out of many small Plums, and intertwining Lemons on a branch with the letters, Caille simply overprinted the letters in the same style on all the symbols.
Here, the bar was a stick of Liberty Fruit Chewing Gum, at a 45 degree angle, with a patriotic shield symbol.
The apple, with a stem above it, looked like it might have actually been a single cherry, but the same drawing, with "Apple" on a green bar across it, appeared in the later Caille Victory Bell, so I can only accept that it was intended to be an apple.
The second set of payout symbols was used with versions of the Operator's Bell that replaced the bell symbol with another fruit, the pineapple, to further emphasize the machine's role as a gum vendor, as opposed to a gambling device.
The third set of payouts in this illustration are those of the Caille Victory Bell, which is of historical interest as the apple, strawberry and pineapple made their appearance again as three of the additional fruit symbols used when Adolph Caille founded A. C. Novelty and brought out the innovative and unusual Multi-Bell Seven-Way, to be discussed below.
Note that while the Liberty Bell remained a symbol on this machine, it took over the role of the bar, while the pineapple took over that of the bell. On the other hand, plums (as well as the lemon) kept their original role, but were drawn differently, the symbol depicting a pair of plums rather than a single plum.
The Victory Bell was made during the Second World War; or, rather, since metals were critical war materials, older machines were converted to this type with new reel strips.
Other early Caille machines used other fruit symbols in a different way:
The fourth set of payouts are those of the Caille Little Merchant, as well as the nearly-identical Watling O.K. Deluxe. Note that here, bananas replace the cherries, pineapples replace oranges (instead of bells), pears replace the plums, grapes replace the bells, and strawberries replace bars (instead of oranges). The lemon retains its identity, but is drawn differently, at an angle and on a branch.
And on one occasion, Caille took the standard Mills fruit symbols, and had a bit of fun with them, surrounding each symbol with a dynamic-looking frame. This is illustrated in the fifth set of payouts, belonging to a machine from 1934 which was no doubt terribly embarassing in hindsight, the Caille Dictator.
The sixth set of payouts are those of a smaller machine with a wooden case, the Caille Merchant. In addition to avoiding confusion between the Caille Little Merchant and the Caille Merchant, there was also a much later small machine by Jennings called the Little Merchant. Note how the bar is now drawn as a stick of gum at an angle, depicted as a three-dimensional object.
A number of books about slot machines, or about gambling in general, refer to a persistent myth that it is possible for operators to just turn a screw somewhere in a slot machine to adjust its payout percentage. Instead, they note, it would be necessary on a mechanical slot machine to change the symbols on the reel strips, and also change the disks with holes in them which indicate to the mechanism which symbol is on each reel in a given position in a corresponding manner.
One might be able to change a machine's percentage slightly with a screwdriver by changing how large the maximum size of the jackpot is allowed to be.
That sounds very sensible to me, particularly as those accounts did include the qualification that something like that might be possible if the machine was rigged.
However, I have encountered what may be the source of this rumor.
An early Caille catalog, in its entry for the Caille Liberty Bell, contains the following statement:
"Percentage regulator changes profits from 25% to 50% without change of reward card."
While the machine could have come with an alternate set of reel strips, this certainly does sound like the kind of adjustment that was rumored.
However, I have found more information in a book about the 1911 session of the California legislature. At that time, both Mills and Caille upright machines had in them a two-position lever which, when set in the higher percentage position, prevented the rarer colors with higher payouts from coming up when they were played, but they could still come up if the colors at lower odds were palyed instead. So appareently the "percentage regulator" on a slot machine would make it behave as if it were "bugged".
Before turning to the chief topic of this section, to introduce the ideas it uses, I would like to examine another unusual slot machine that is less well known, the Alwin by Buckley, also sold as the Deluxe Cent-a-Pack. (There was also a plain Cent-a-Pack which was a normal three-reeler.)
This machine had four reels.
The first reel had a number indicating a prize amount, such as 4, 5, 10, 15, 20 or 30.
The remaining three reels had the symbols of a conventional slot machine, such as cherries, oranges, lemons and bells.
If three of any symbol showed on the pay line, one received the payout amount shown on the first reel, except that three bars still paid a jackpot of 50.
There was also a four-reel machine called "The New Deal" by Pace which may have been similar; some of those machines had the payout amount on the first reel like the Alwin, and others had it on the fourth reel. (There was also a three-reel conventional slot machine version, and a five-reel one with playing card images on the reels, which paid off for poker hands, so they used this name for machines of different kinds.)
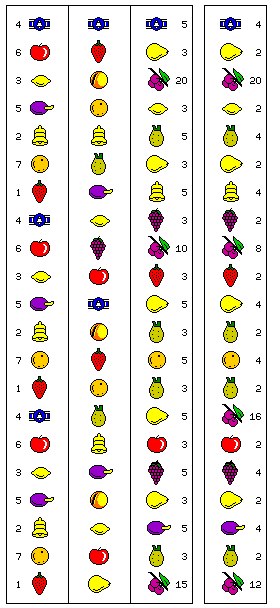

An unusual slot machine, called the Multi-Bell Seven Way was devised by Adolph Caille after he had sold the Caille Brothers slot machine business, and so he started a new company, A. C. Novelty, to produce and sell it. (Eventually, the company was renamed to A. C. Manufacturing during the 1950s.) The machine is pictured on the left.
It had twelve different kinds of symbols; the seven which could form a jackpot combination, and on which the player could wager: Strawberries, Bells, Lemons, Bars, Plums, Apples, and Oranges, and five others: Cherries, Pears, Apricots, Grapes, and Pineapples, which only appeared on the second and third reels.
The player could choose which one of the first seven symbols to wager on, and would win a prize if that symbol came up on the first reel. The amount of the prize was indicated on the last reel; it might be anything from twice to 20 times the amount wagered.
If three of the symbol chosen by the player came up, then a jackpot would be paid out.
The payout odds were given on the third reel along with the third symbol; those odds were not the same for every occurrence of the same symbol.
The diagram to the right shows the arrangement of the symbols on its reel strips as I had reconstructed it from images of the machine, as well as from a couple of videos of the machine I had encountered.
The videos were of the version with larger numbers on the third reel; later, I saw an image of the actual reel strips for the version with smaller numbers, which confirmed my reconstruction of the first two reels, which apparently are the same in both versions, and so now the image at right shows both versions of the strip for the third reel.
The second reel had two copies of each of those seven symbols printed on their reel strips, as well as seven other symbols, and the third reel only one of each of those symbols: even so, in order for jackpots to be rare, it was still necessary that only three of the chosen symbol could pay a jackpot. On the second reel, the extra symbols were one bunch or grapes, one pear, two pineapples, and three apricots, according to one source I found; but this source also claims, incorrectly, that cherries do not appear on the third reel.
While three of any of the seven fruit symbols on which the player could wager would constitute one of the seven jackpot combinations offered by the machine, players were only eligible for the jackpots corresponding to the symbol, or symbols, on which they wagered. It was still necessary to reduce the frequency of jackpot combinations, and so the middle reel operated as a 14-stop reel; that is, one out of every three positions printed on the reel strip could not actually appear on the pay line.
It is not surprising, unfortunately, that this machine was not a great success at the time. It was ungainly and unattractive in appearance, while conventional slot machines were competing to attract the eye. More important, its play was both unfamiliar and complicated. Due to its uniqueness and rarity, however, it is highly sought after by collectors today.

This machine hearkened back to the early days of coin-operated gambling devices before Charles Fey invented the slot machine as we know it today. Basically, a typical upright was a coin-operated version of a Wheel of Fortune. The player can choose to wager on a color that only appears a few times on the wheel, to win a large prize if it comes up, or on colors that appear more often for lower prizes.
One of the earlier such machines was the Mills Owl, pictured at right, with the picture retouched by hand to make the colors of the segments of the wheel visible. It was a successor to their earlier Klondyke from 1897.
The Mills Owl had a wheel with 50 colored segments, in five different colors.
The breakdown of colors and their payouts were:
Red 18 2 Black 18 2 Yellow 8 5 Gray 4 10 Green 2 20
The first column shows the color, the second the number of spaces on the wheel that are that color, and the third the payout in coins if that color came up and was the color on which the player bet by inserting a coin in the associated slot.
An even-money bet on red or black would return 36 coins out of every 50, for a house advantage of 28%.
The other bets return 40 coins out of every 50, for (surprisingly) a lower house advantage of 20%.
The green spaces on the wheel, a dark green in color, also had an owl symbol on them, which would later become the Mills trademark.
One thing I haven't done much so far is to provide an overview of the history of slot machines as a whole as an enterprise; this page started with a focus on how the payout schedules of slot machines evolved, and not on other aspects of the story.
After Charles Fey invented the first three-reel automatic payout slot machine in San Francisco, the 1906 San Francisco earthquake prevented him from gradually, with his new invention, acquiring the ability to establish a major slot machine manufacturer.
Mills, Caille, and Watling were, at the time, all established manufacturers of upright coin-operated gambling machines like the Mills Owl shown above. Mills was the first company to begin making the new slot machines that Charles Fey invented; apparently, this was with Charles Fey's direct assistance in return for a supply of the initial production to sell and re-establish himself in business.
Caille and Watling later also entered the field, and despite competition between those companies, apparently the technology was shared on amicable terms. Also, for a time, Charles Fey was employed by the Watling firm.
O. D. Jennings was a Mills salesman, and Ed Pace had a business selling used slot machines, before they entered into the manufacture of slot machines, founding two more of the early firms in the business. Other firms, like Buckley, had similar origins much later on.
As may be apparent from what is present elsewhere on these pages, Mills was the largest company in the slot machine business, and was responsible for numerous innovations.
Caille, Jennings, and Pace came out with a few innovations of their own, and generally tried to keep up with Mills in features and styling.
After making what was perhaps the most beautiful slot machine ever made, the Rol-a-Top, Watling, on the other hand, while it did keep up with changes to payout schedules and other features, like "future pay", decided it couldn't really improve on perfection. And so, while there were the Diamond Front and Castle Front versions of the Rol-a-Top, it largely didn't change over the years from 1935 to 1950, and Watling was significantly behind the other major slot machine companies in sales.
However beautiful a slot machine may look, the passing customer will be more confident that a modern-looking one will actually work when he puts his coin in the slot and pulls the lever. And so shiny chrome machines from Pace and Jennings that were plain in comparison pulled ahead.
It has been noted above that the Caille brothers sold out to retire, and then returned to the field with a very innovative machine that was not sufficiently successful to permit the founding of a major new slot machine producer, although it seems to have enjoyed at least a modest degree of success, sufficient to permit a few variations on the design to be produced.
Mills and Jennings attempted to stay in the field when casinos switched to using electromechanical slot machines, but they were not able to do so, leaving Bally unchallenged. But then Bally in its turn succumbed to other companies achieving dominance when the switch was made to fully electronic slots, either using reels as indicators only, or with video displays.

The Mills Futurity slot machine, pictured at right, is popular with slot machine collectors. It had the feature that if one went ten consecutive plays without a win, one would get one's ten coins back. Since some wins paid less than ten coins, it was still possible for the machine to make a profit.
One way to help that along would simply be to make the lower payments particularly common. However, the Mills Futurity went further than that; it was a "ten-stop" machine of a very special kind.
That is, although there were twenty symbols printed on each wheel, the wheels could actually only stop on ten of them.
Ten-stop slot machines were a common form of crooked slot machine in the old days. However, the Mills Futurity had a difference: depending on where the indicator of consecutive non-winning plays pointed, a different set of ten symbols was available.
The Pace Kitty, a machine inspired by the Mills Futurity, and intended to compete with it, did not resort to any such technique; however, it funded the jackpots which it paid out after ten losing plays by putting "kitty" symbols on the first reel which could not be part of any winning combination.
The Mills Futurity worked like this:
Usual set of Alternate set
symbols of symbols (4 or 10 losing plays)
(*) Lemons - - 3 - - -
(%) Cherries 1 1 - 8 8 -
(O) Oranges 3 3 1 - - 5
(@) Plums 2 1 1 - - 3
(A) Bells 0 5 4 1 1 1
(=) Bars 4 0 1 1 1 1
Another variation of the Mills Futurity existed with the Gold Award symbol as well: and one version of the reel strips for that machine are like this:
Usual set of Alternate set
symbols of symbols (5 or 10 losing plays)
(*) Lemons 1 - 3 - - 1
(%) Cherries 1 1 - 8 8 -
(O) Oranges 1 3 1 - - 4
(@) Plums 2 1 1 - - 3
(A) Bells 1 1 1 - - -
(=) Bars 4 0 1 1 1 1
(o) Award - 4 3 1 1 1
On pulls 4 and 10, the winning combinations of three bells and the jackpot, three bars, were at least possible, so one could consider the machine to not actually be rigged in an outright fashion. Incidentally, the cheating mechanism could be removed from the machine, and so it may be useful to examine the result of doing so.
The payout odds for this machine, for the different kinds of pull, are shown below:
Usual Pulls 4 and 10 Combined
%%. 3 1 * 1 * 3 * 3 = 9 8 * 8 * 9 * 3 = 1728 9 * 9 * 12 * 3 = 2916
%%*, %%A 5 1 * 1 * 7 * 5 = 35 8 * 8 * 1 * 5 = 320 9 * 9 * 8 * 5 = 3240
OOO, OO= 10 3 * 3 * 2 * 10 = 180 3 * 3 * 8 * 10 = 720
@@@, @@= 14 2 * 1 * 2 * 14 = 56 2 * 1 * 5 * 14 = 140
AAA, AA= 18 1 * 1 * 2 * 18 = 36 1 * 6 * 6 * 18 = 648
=== 20 1 * 1 * 1 * 20 = 20 5 * 1 * 2 * 20 = 200
--- ---- ----
280 2104 7854
with three bars also paying off the jackpot.
So normally it only pays 28% of what it takes in, but on the fourth and tenth spins, it pays out more than twice what it takes in.
In the case of the Gold Award machine, the payouts are:
Usual Pulls 5 and 10 Combined
%%. 3 1 * 1 * 6 * 3 = 18 8 * 8 * 9 * 3 = 1728 9 * 9 * 15 * 3 = 3645
%%*, %%A 5 1 * 1 * 4 * 5 = 20 8 * 8 * 1 * 5 = 320 9 * 9 * 5 * 5 = 2025
OOO, OO= 10 1 * 3 * 2 * 10 = 60 1 * 3 * 7 * 10 = 210
@@@, @@= 14 2 * 1 * 2 * 14 = 56 2 * 1 * 6 * 14 = 168
AAA, AA= 18 1 * 1 * 2 * 18 = 36 1 * 1 * 3 * 18 = 54
=== 20 1 * 1 * 1 * 20 = 20 5 * 1 * 2 * 20 = 200
ooo 50 1 * 1 * 1 * 50 = 50 1 * 1 * 1 * 50 = 50
--- ---- ----
190 2118 6352
Three bars also pays the jackpot. The Gold Award does not pay a jackpot, but is instead a fixed prize that is paid in the form of a "Gold Award" token to be redeemed with the merchant. That prize might be 20, 50, 75, or 100 coins, depending on the machine. The calculation above was made assuming the Gold Award prize to be 50 coins; however, I have found that reproduction award cards stating the Gold Award to be 75 coins appear to be the ones currently most offered for sale.
If the cheating mechanism is taken out, then, in the absence of the Futurity feature, and not considering jackpots, the machine would be profitable, but it would have a low percentage in the case of the basic machine; in the case of the Gold Award machine, however, the percentage would be a more usual one of 20.6% in the absence of jackpots.
To figure out the actual percentage of the machine, one has to follow the sequence of events from the first pull. To keep the numbers reasonable, I will scale things to 1000 plays at the beginning, allowing fractional values for the additional spins, rather than either using more decimals and stating things in terms of a single play, or ensuring all numbers are integers by counting over 10 to the 30th power sequences.
Usual: 1000 combinations, 32 winning, 968 losing Pulls 4 & 10: 1000 combinations, 643 winning, 357 losing
Thus, one has:
Pull
1) 32 chances of an average win of 280/32, on an expenditure of 1 coin
2) 968/1000 * 32 chances of an average win of 280/32, on an expenditure of 2 coins
3) (968/1000)^2 * 32 chances of an average win of 280/32, on an expenditure of 3 coins
4) (968/1000)^3 * 643 chances of an average win of 2104/643, on an expenditure of 4 coins
5) 357/1000 * (968/1000)^3 * 32 chances of an average win of 280/32, on an expenditure of 5 coins
6) 357/1000 * (968/1000)^4 * 32 chances of an average win of 280/32, on an expenditure of 6 coins
7) 357/1000 * (968/1000)^5 * 32 chances of an average win of 280/32, on an expenditure of 7 coins
8) 357/1000 * (968/1000)^6 * 32 chances of an average win of 280/32, on an expenditure of 8 coins
9) 357/1000 * (968/1000)^7 * 32 chances of an average win of 280/32, on an expenditure of 9 coins
10) 357/1000 * (968/1000)^8 * 643 chances of an average win of 2104/643, on an expenditure of 10 coins
357/1000 * (968/1000)^8 * 357 chances of the return of the 10 coins played
Thus, the percentage for one complete series of pulls, long or short, until a prize is returned can be worked out:
Pull
Expenditure Return
1) 1000 280
2) 968 271.04
3) 937.024 262.36672
4) 907.039232 1908.410544
5) 323.813006 90.667642
6) 313.450990 87.766277
7) 303.420558 84.957756
8) 293.711100 82.239108
9) 284.312345 79.607457
10) 275.214350 579.050992
982.515229
----------- -----------
5605.985581 4708.621725
Since by that time, one has spent almost 4,000 coins, quitting after the fourth pull, which returns half of them, is not profitable, although it's less bad than quitting after any of the first three pulls. Similarly, if one goes past the fourth pull, it pays to continue until the tenth pull.
Thus, exclusive of jackpots, it pays out 83.99% of what it takes in, for a percentage of 16.01%, which is not bad for a slot machine that is "rigged". And this does not even count any jackpot paid in addition to the 18 coins for three bars.
Of course, the machine does pay out jackpots. If we assume that the jackpot consists of 100 coins, the number of coins paid for jackpots - which can only happen on the fourth and tenth plays - can be calculated in the same fashion:
Pull 4) (968/1000)^3 * 1 chance of a win of 100 10) 357/1000 * (968/1000)^8 * 1 chance of a win of 100
giving the following increment on the return:
Pull
Return
4) 90.703923
10) 27.521435
-----------
118.225358
This amounts to 2.11% of what was spent, so the payout is increased to 86.1%, reducing the machine's percentage to 13.9%. For other values of the jackpot, the change to the percentage scales linearly, as the jackpot amount does not affect which spins win.
From one source, it appears that the Gold Award version of this machine switched to the alternate symbols on the fifth and tenth spins instead of the fourth and tenth spins. This could have the effect of increasing the percentage of the machine, at least if otherwise it would be worthwhile to quit after the fourth spin: but since it has a higher percentage for the house on the normal spins, it is unclear why this change would be needed.
As I'm not aware that anyone else has attempted to calculate the percentage of a Mills Futurity slot machine, I've decided that it's probably worthwhile to attempt to calculate the percentage for the Gold Award version of it as well.
So, repeating the calculation:
Usual: 1000 combinations, 22 winning, 978 losing Pulls 5 & 10: 1000 combinations, 642 winning, 358 losing
Thus, one has:
Pull
1) 22 chances of an average win of 190/22, on an expenditure of 1 coin
2) 978/1000 * 22 chances of an average win of 190/22, on an expenditure of 2 coins
3) (978/1000)^2 * 22 chances of an average win of 190/22, on an expenditure of 3 coins
4) (978/1000)^3 * 22 chances of an average win of 190/22, on an expenditure of 4 coins
5) (978/1000)^4 * 642 chances of an average win of 2118/642, on an expenditure of 5 coins
6) 358/1000 * (978/1000)^4 * 22 chances of an average win of 190/22, on an expenditure of 6 coins
7) 358/1000 * (978/1000)^5 * 22 chances of an average win of 190/22, on an expenditure of 7 coins
8) 358/1000 * (978/1000)^6 * 22 chances of an average win of 190/22, on an expenditure of 8 coins
9) 358/1000 * (978/1000)^7 * 22 chances of an average win of 190/22, on an expenditure of 9 coins
10) 358/1000 * (978/1000)^8 * 642 chances of an average win of 2118/642, on an expenditure of 10 coins
358/1000 * (978/1000)^8 * 358 chances of the return of the 10 coins played
Thus, the percentage for one complete series of pulls, long or short, until a prize is returned can be worked out:
Pull
Expenditure Return
1) 1000 190
2) 978 185.82
3) 956.484 181.73196
4) 935.441352 177.733857
5) 914.861642 1937.676958
6) 327.520468 62.228889
7) 320.315018 60.859853
8) 313.268087 59.520937
9) 306.376189 58.211476
10) 299.635913 634.628864
1072.696569
----------- -----------
6351.902670 4621.109363
So in this case, the machine returns 72.75% of what is put in, for a profit of 27.25%, which, again, is highly reasonable for a slot machine. This is based on the assumption that the Gold Award payout is 50 coins, but excludes any jackpot paid on the three bars. It is, however, a higher percentage, as anticipated, than that of the plain version.
As both three Gold Award symbols and three bars occur on only one combination, and only for the fifth and tenth spins, the same calculation will let us determine how to adjust the percentage for the amount of the jackpot and for a change in the size of the Gold Award from the value of 50 that was assumed.
Again, for a jackpot of 100:
Pull 5) (978/1000)^4 * 1 chance of a win of 100 10) 358/1000 * (978/1000)^8 * 1 chance of a win of 100
giving the following increment on the return:
Pull
Return
5) 91.486164
10) 29.963591
-----------
121.449756
which is 1.91% of what was spent, so for a Gold Award of 50 coins and a jackpot of 100 coins, the return is increased to 74.66%, and the profit decreased to 25.34%. Again, for any other change in the sum of the Gold Award and the jackpot, the change scales linearly.
Incidentally, it might be asked why the choice of a particular sequence of pulls, the one starting from the indicator being at zero, and ending with either a prize being won from the reels, or the prize from the indicator hitting ten being won, produces a percentage that can be meaningfully called "the percentage" of that slot machine.
Of course, this choice can be easily justified. Since the indicator is reset to zero immediately following either the reels awarding a prize, or ten coins being returned because the indicator has reached ten, a very long sequence of consecutive pulls on the machine would, except for short sequences of pulls at the beginning and end, consist of a series of this kind of sequence one after another. Thus, the percentage for that kind of sequence is indeed the limiting value for a sufficiently long sequence of pulls.
This is the sort of thing that is too obvious for words... at least if one is a mathematician.


Another interesting machine from Mills was the Bonus; this had the letters of the word "BONUS" overprinted on five of the symbols on the first reel, and as they appeared, one at a time in order, the word "BONUS" built up in a display at the top. When the word was completed, a special payout of 18 coins was made. An early Mills Bonus slot machine, with the Horsehead style of case, is shown on the left.
This machine remained popular for some time, and thus the BONUS feature continued to be offered in Mills' later machines. The machine illustrated on the right is such a machine, in the "hi-top" style. This style of machine was first introduced in 1947, with the Mills Jewel Bell.
The very first Mills Bonus machines actually used a 10-stop structure similar to that of the Futurity, but in their case, they alternated between the odd and even stops on odd and even plays. This was apparently intended to prevent a lucky player from completing the word BONUS in only five spins. However, a year or two later, either it was recognized that the risk involved of making it appear that these machines were rigged outweighed this issue, or, perhaps even more likely, it was decided that the chance of obtaining the letters B-O-N-U-S in a small number of spins was so low that attempting to avoid that improbable occurence did not justify the extra cost of this mechanism, and so subsequent Mills Bonus slot machines worked in the conventional manner as normal 20-stop machines.
In the case of the conventional Mills Bonus machines, the reels contained the following symbols:
(*) Lemons 4 - 4 (%) Cherries 6 7 - (O) Oranges 3 5 6 (@) Plums 5 1 6 (A) Bells 1 5 3 (=) Bars 1 2 1
Given the payouts of
%%. 3 %%*, %%A 5 OOO, OO= 10 @@@, @@= 14 AAA, AA= 18 === 100
we can calculate how many coins this paid out for each 8000 coins put in, on average:
Reel Combinations Value Amount
1 2 3 Paid
6 * 7 * 13 = 546 * 3 = 1638
6 * 7 * 7 = 294 * 5 = 1470
3 * 5 * 7 = 105 * 10 = 1050
5 * 1 * 7 = 35 * 14 = 490
1 * 5 * 4 = 20 * 18 = 360
1 * 2 * 1 = 2 * 100 = 200
----
5208
As for the BONUS payments, what proportion of the coins put in do they correspond to?
Assuming a player comes to a machine with no letters showing in the annunciator, and plays, with the normal return of 5208 coins out of every 8000 coins played, how long, on average, will it take for the BONUS combination to complete, returning an extra 18 coins?
Well, since at each step, one particular letter, with one chance of 20 in coming up, is what is needed to advance to the next state, that time is five times as long as it takes for one symbol that appears only once out of 20 possibilities to come up.
Rather than a complicated calculation of the powers of 19/20, however, this suggests that if one treated the BONUS prize as a prize of 18/5 coins, paid whenever the letter B came up, the percentage would be the same.
So that would be 18 coins back from every 100 coins played, or 1440 coins back from every 8000 coins played.
The payouts of the earliest BONUS machines were different:
%%. 3 %%*, %%A 10 OOO, OO= 10 @@@, @@= 14 AAA, AA= 18 === 50
And the symbols on the two halves of each reel were:
Symbols together with Symbols with no
the letters B-O-N-U-S letters
(*) Lemons - - - 2 - 4
(%) Cherries 4 5 - 1 3 -
(O) Oranges 1 2 4 2 1 3
(@) Plums 1 - 5 3 1 1
(A) Bells 3 2 - 2 1 1
(=) Bars 1 1 1 0 4 1
So for every 1000 coins put in when the letters could turn up, one can calculate what is paid out:
Reel Combinations Value Amount
1 2 3 Paid
%%. 4 * 5 * 10 = 200 * 3 = 600
OOO,OO= 1 * 2 * 5 = 10 * 10 = 100
AA= 3 * 2 * 1 = 6 * 18 = 108
=== 1 * 1 * 1 = 1 * 50 = 50
----
850
And for every 1000 coins put in when the letters could not turn up, what is paid out is:
Reel Combinations Value Amount
1 2 3 Paid
%%. 1 * 3 * 5 = 15 * 3 = 45
%%A,%%* 1 * 3 * 5 = 15 * 10 = 150
OOO,OO= 2 * 1 * 4 = 8 * 10 = 80
@@@,@@= 3 * 1 * 2 = 6 * 14 = 84
AAA,AA= 2 * 1 * 2 = 4 * 18 = 72
----
431
which means the machine paid back 1,281 out of every 2,000 coins, or only 64.05%, not including the BONUS award.
Instead of a letter coming up 1/20 of the time on every spin, it comes up 1/10 of the time on half the spins, so it may still be reasonable to treat its value as 18 coins out of every 100, thus giving the machine an 82% payout.
I have been informed that it was possible to change a cam on this machine, so that instead of the two sets of symbols alternating with every turn, the pattern could be changed, presumably to make the symbols without the letters B-O-N-U-S, and with a lower payout percentage, more likely at the discretion of the operator.
Also, while this special mechanism was used only on the Horsehead style of Bonus Bell, and not on the Hi-Top style, it's important to note that most Horsehead Bonus Bells did not have the special mechanism, so this type of machine is quite rare. Also, before the Hi-Top version of the Mills Bonus Bell came out, but after the end of World War II, Horsehead Bonus machines were introduced in the 50 cent denomination; none of these would have had that mechanism.
It may also be noted that SEGA at one point, much later, made a slot machine that was inspired by the Mills Bonus Bell. It had an electrical display on which the letters B-O-N-U-S lit up one by one; but the display was advanced by an "Advance Bonus" symbol coming up on the first reel, not by the next letter coming up. Of course, either way, there was one position on the reel that advanced the bonus, even if in the original design that position changed at each step, so this in itself would not affect the odds.

As for the Pace Kitty, pictured at right, the symbols on its reels are:
(^) Kitty 4 - - (*) Lemons - - 4 (%) Cherries 8 7 - (O) Oranges 2 6 6 (@) Plums 4 2 5 (A) Bells 1 3 3 (=) Bars 1 2 1
The conventional payouts were:
%%. 2 %%*, %%A 4 OOO, OO= 8 @@@, @@= 12 AAA, AA= 16 === 70
assuming the jackpot to be 50 coins, in addition to the regular 20-coin payout for three bars.
Since a Kitty symbol on the first reel caused one coin to be added to the Kitty, which would eventually be returned to the player after 10 losing plays in a row, it can be treated as a combination that rewards one coin to the player. That would, however, lead to an inaccurate calculation of the percentage if the Kitty was likely to overflow before it was paid out. The Kitty had a capacity of 50 coins.
Performing that calculation:
Reel Combinations Value Amount
1 2 3 Paid
^.. 4 * 20 * 20 1600 * 1 = 1600
%%. 8 * 7 * 13 = 728 * 2 = 1456
%%*, %%A 8 * 7 * 7 = 392 * 4 = 1568
OOO, OO= 2 * 6 * 7 = 84 * 8 = 672
@@@, @@= 4 * 2 * 6 = 48 * 12 = 490
AAA, AA= 1 * 3 * 4 = 12 * 16 = 192
=== 1 * 2 * 1 = 2 * 70 = 140
----
6118
for a total payout percentage of 76.48%.
Excluding the combination with a Kitty on the first reel, there were 1,266 winning combinatins out of the 8,000 possible combinations. So the chance of ten combinations in a row that did not win would be about 17.8%, which would make it unlikely that, with a 20% chance of adding one coin in every spin, that more than 50 coins would accumulate in the Kitty.
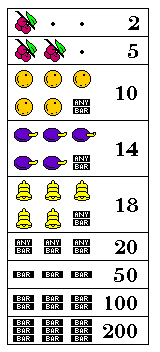

So far, we have looked only at fully mechanical slot machines, which, of course, are no longer in use.
The sixth set of payouts in the second row of the large illustration near the top of this page are those of the Bally 742A slot machine. They are almost identical to the payouts of the Mills 21 Bell, except that the payout for three melons is larger, and the 7 is now an ordinary symbol occupying a space on the reel in its own right, rather than being overprinted on anything else.
Today's slot machines often have single, double, and triple bar symbols on them, and so I thought I would look for where this started.
The Bally 809, from 1967, was the first machine to allow you to put in from one to five coins for a single spin, multiplying the prizes by the number of coins paid, although an earlier machine from Bally, the Double Up, also known as the Bally 808, allowed one to play one or two coins in this manner.
It was an electromechanical slot machine. That is: the spin of the reels was still the actual randomizing element which decided if a play would win or not. But instead of each reel being associated with a disk with holes, so that three reels with the same symbol would allow a rod to go through three corresponding holes, instead the reels were associated with disks that had notches the depth of which indicated what symbol was printed on the reel strip in each position. The notches allowed a wiper to move and make electrical contact with the one of several contacts that corresponded to the symbol.
This design was first used by Bally in 1946, on the Bally Triple Bell console machine, shown to the right, which meant that, although competing slot-machine makers were still slow to adopt the innovation, it was possible for them to do so when they saw the need as the patents would have expired.
The Bally 809 also had the single, double, and triple bar symbols so common on slot machines today. This machine was one of the earliest to use the double and triple bar symbols, along with the Double Up from 1966. The "Any Bar" symbol used on the actual machine's payout chart to indicate that a single, double, or triple bar may appear in that position is used here, consisting of the words "Any Bar" on two short bars.
The payout percentage of 82.5% was identical on the Bally "Money Honey" slot machine from 1963, which was the first electromechanical slot machine in the conventional format, as opposed to console machines such as the Triple Play. It did not include the multiplier feature, and used a different set of symbols on its reels, not including the double or triple bar.
The Money Honey machine, also known as the Bally 742, is also of interest. One of the symbols was a drawing of a girl's face, the titular "Money Honey". This symbol paid 18 coins if it appeared in any of the three visible positions on all of the three reels, except for paying a jackpot if all three appeared on the pay line; thus, this machine can be thought of as another descendant of the Buckley Criss-Cross. On one version of the machine, a jackpot was also paid for a bar on each of the three reels in any position, but that one had cherries on the third reel.
The symbols on its reels are:
(%) Cherries 2 5 - (O) Oranges 4 1 10 (@) Plums 5 1 5 (A) Bells 1 8 1 (=) Bars 1 1 1 (*) Stars 2 1 1 (C) Melons 4 2 1 (&) Girls 1 1 1
The machine's payouts were:
%.. 2 %%. 5 OOO, OO= 10 @@@, @@= 14 AAA, AA= 18 === 150 *** 100 CCC 50 &&& 200
in addition to those for the bars and faces in any position, and so the payout percentage can be calculated as follows:
Reel Combinations Value Amount
1 2 3 Paid
%.. 2 * 15 * 20 = 600 * 2 = 1200
%%. 2 * 5 * 20 = 200 * 5 = 1000
OOO, OO= 4 * 1 * 11 = 44 * 10 = 440
@@@, @@= 5 * 1 * 6 = 30 * 14 = 420
AAA, AA= 1 * 8 * 2 = 16 * 18 = 288
=== 1 * 1 * 1 = 1 * 150 = 150
*** 2 * 1 * 1 = 2 * 100 = 200
CCC 4 * 2 * 1 = 8 * 50 = 400
&&& any 3 * 3 * 3 = 27 - 1 = 26 * 18 = 468
&&& 1 * 1 * 1 = 1 * 200 = 200
----
4766
and so it returned 4766 coins out of 8000, for a payout percentage of 59.575%, and thus a profit of 40.425%, however, as there are multiple payout variations of this machine, I may have used the reel strips for a different set of payouts for my calculation.
Thus, for example, if, despite the fact that the example I found called for a cherry to be on the third reel, one changed the payout for three bars to be 100 coins for the three bars in any position, instead of 150 coins for them on the center line, that would add 2650 coins, leading to a payout of 7316 coins from every 8000, still profitable, for a payout percentage of 91.45%. But that is now higher than the 82.5% claimed for the machine.
Having three different kinds of bars, and having a payout of 20 coins (or, for that matter, 18 coins) for any mixture of those three different kinds of bars is, of course, reminiscent of having a payout of 18 or 20 coins for only one kind of bar, but in three different positions.
Of course, there is one important difference: instead of 27 possibilities of which one is a jackpot, now there are 27 possibilities of which three are jackpots.
The 809 had a multiplier feature, where one could wager one to five coins on a single pull of the handle. Thus, it did not have another feature which has since become common on the slot machines today: the 5-line pay progressive feature, where one can pay more than one coin in order to win on additional lines in the window in addition to the center line. This feature also existed on the Bally electro-mechanical slot machines; the Bally 922, from 1971, was one machine with progressive 5-line play. The Bally 831, from 1968, had progressive 3-line play; the first coin won on the conventional pay line, the second on the line above, and the third on the line below. The 922 continued the pattern with the fourth coin paying on the diagonal line going from the top left to the bottom right, and the fifth coin paying on the diagonal from the bottom left to the top right. The jackpot for three sevens was higher for a win on the fifth line, as an inducement to play more coins.
While three bars in any position wouldn't work with that feature, three different kinds of bars instead would be perfectly compatible. Hence, it seems to me that the slot machines of today can trace some of their typical features through to the early Bally electromechanical machines, and beyond them to the fully-mechanical Buckley Criss-Cross.
Although the Bally 922 didn't have the double and triple bar symbols, the Jennings 400 was one example of an electro-mechanical slot machine that combined those symbols with 5-line play. I have seen one source which stated that the Bally Triple Bell allowed 3-line play, but as far as I can tell from looking at images of it, it offered a multiplier feature, and the ability to play using three different denominations of coins, but not 3-line play.
Incidentally, while Bally introuduced the currently popular single, double, and triple bar symbols, the idea of having multiple kinds of bar on a slot machine was introduced at an earlier point. Some Jennings Standard Chief machines used in casinos had both ordinary bars, and special bars - the special bars could both substitute for an ordinary bar, and provide a larger payout if one had three special bars in a row.
The special bars were surmounted by an Indian head of similar form to the one which adorned the cases of earlier pre-war Jennings slot machines from the first Jennings Chief onwards.
The same head design, but in full color instead of metallic grey, without a bar behind it, appeared on the first reel of early Jennings "Wild Indian" machines. Later, a cartoony full-figure image of an agitated brave in buckskin breeches replaced it.
Mills had a Deuce Wild slot machine both in Chrome Bell and Hi-Top models, and there was a Wild Lemon console by Bally, so a symbol on the first reel that could substitute for anything, just as a bar on the third reel could substitute for several things, was another added feature on some slot machines.
In the case of Bally's Wild Lemon console from 1947, however, the lemon only qualified as a wild symbol when the "Wild Lemon" light on the console was lit, not on every pull.
For whatever reason, the 2 on the Mills Deuce Wild machine was overprinted on a bell symbol, instead of standing alone; whether to add visual interest, or for consistency with the 21 Bell (although as that one first appeared as a Hi-Top machine, while there are Chrome Bell Deuce Wild machines, that hardly seems possible, but payout schedules can be retrofitted) or on general principles of some sort is not clear.
The Mills machine even had a payout schedule that explicitly showed the 2 substituting within every possible winning combination. So on the right I show such schedules for all three of these machines, although the other two did not. The actual payout schedule on the Mills machine just used a printed digit 2 rather than showing the symbol as it appeared on the reels - and like most payout schedules on slot machines, it was largely in the reverse of the order I use, starting with the larger prizes and working down to the smaller ones.
Of course, while it hardly needs to be said, as it is well known, it should at least be mentioned, if only for reasons of acknowledgement, that from the 1930s to the 1960s, unlike today, nothing was considered amiss in the commercial use of Native American imagery, as though American Indians, like, say, ancient Egyptian Pharaohs, were figures of the distant history of ancient times... rather than a group of people still in existence, whose own views on the matter ought to be consulted. It was as if the concept of "cultural appropriation", so familiar today, had not even yet been raised... which, I suspect, is not entirely true, even if the phrase was not coined, and the idea was little heeded.
Another example of an early machine with the single, double, and triple bar has its payouts shown at left; this was an electronic slot machine from 1979, the Sircoma Fortune Triple Bar Special.
Let us suppose that we wished to create a slot machine with a payout schedule like the following:
%.. 2 %%. 4 %%%, %%*, %%A, %%= 8 OO. 10 OOO, OO= 20 @@. 12 @@@, @@= 24 AA. 14 AAA, AA= 28 === 50 *A* 50
The idea is to provide a payout schedule that is very generous, combining the classic and modern approaches to cherries, and also modifying the payouts for the orange, plum, and bell so as to make a three-reel machine behave almost like a four-reel machine.
Can a reasonable distribution of symbols on the reel strips produce a profitable slot machine with this payout schedule?
It isn't easy, but if one takes the extreme measure of putting only one cherry on the first reel, it is barely possible:
If the symbols on the reels are distributed as follows:
(*) Lemons 6 0 1 (%) Cherries 1 6 6 (O) Oranges 5 1 6 (@) Plums 1 6 5 (A) Bells 6 1 1 (=) Bars 1 6 1
then, the result is:
Reel Combinations Value Amount
1 2 3 Paid
1 * 14 * 20 = 280 * 2 = 560
1 * 6 * 11 = 66 * 5 = 330
1 * 6 * 9 = 54 * 8 = 432
6 * 1 * 13 = 78 * 10 = 780
6 * 1 * 7 = 42 * 20 = 840
1 * 6 * 14 = 84 * 12 = 1008
1 * 6 * 6 = 36 * 24 = 864
6 * 1 * 18 = 108 * 14 = 1512
6 * 1 * 2 = 12 * 28 = 336
1 * 6 * 1 = 6 * 50 = 300
6 * 1 * 1 = 6 * 50 = 300
----
7262
giving a house advantage of just over 9.2%.
Of course, making the machine look like a four-reel machine in terms of how it handles the orange, the plum, and the bell, but having to limit jackpots to 50 coins is to omit the most attractive feature of a four-reel slot machine.
However, if one added just one symbol to the machine's repertoire, providing an additional jackpot for three sevens or three melons, that would make it easy to adjust things to allow room for at least that one jackpot to be more generous. Of course, allowing lemons on the first reel and responding to that by making lemon-bell-lemon a jackpot means there is already one extra jackpot after three bars, but then there are real slot machines with both melons and sevens.
Actually, though, it's obvious that only a drastic measure will salvage this design so as to yield something of practical use.
If the payouts for three oranges, three plums, and three bells are restored to their conventional values, then one could still retain payouts for two oranges, two plums, and two bells at half of that, thus still meeting the goal of having winners more frequently than if matching symbols on all three reels are required for nearly every prize, and now have room for a generous jackpot.
As well, the constraint to a maximum of six of any one symbol on any reel would need to be discarded. This could yield something like this:
(*) Lemons 1 0 1 (%) Cherries 1 9 6 (O) Oranges 8 1 6 (@) Plums 1 8 5 (A) Bells 8 1 1 (=) Bars 1 1 1
Apply to that a payout schedule such as:
%.. 2 %%. 4 %%%, %%*, %%A, %%= 8 OO. 5 OOO, OO= 10 @@. 6 @@@, @@= 12 AA. 7 AAA, AA= 14 === 100 *A* 200
and the result becomes:
Reel Combinations Value Amount
1 2 3 Paid
1 * 11 * 20 = 220 * 2 = 440
1 * 9 * 11 = 99 * 5 = 495
1 * 9 * 9 = 81 * 8 = 648
8 * 1 * 13 = 104 * 5 = 520
8 * 1 * 7 = 56 * 10 = 560
1 * 8 * 14 = 112 * 6 = 672
1 * 8 * 6 = 48 * 12 = 576
8 * 1 * 18 = 144 * 7 = 1008
8 * 1 * 2 = 16 * 14 = 224
1 * 1 * 1 = 1 * 100 = 100
1 * 1 * 1 = 1 * 200 = 200
----
5443
and now the payout percentage is a mere 68.0375%, more like that of a typical slot machine, and allowing some room to adjust things upward. But not enough room to allow even so much as a second cherry on the first reel, so it's still a tight squeeze.

Now, let's look at another possibility. This one is more complicated, so it may not be possible to make a purely mechanical slot machine of ordinary size with such a payout schedule. Perhaps it would instead require at the least an electromechanical console.
Here, the motivation is this:
Unfortunately, despite being creative and ground-breaking, the AC Novelty Seven-Way Multi-Bell did not prove to be a great success in the marketplace, and I presume this is because it was too different and unfamiliar.
The Mills 4 Bells, on the other hand, also let the player choose, to a limited extent, whether to bet on oranges, plums, bells, or bars.
So in a way, it was similar to the Seven-Way Multi-Bell. However, picking a particular symbol only doubled (or, in one case, tripled) the regular prize for that symbol, so it really wasn't that different from a conventional slot machine.
So the idea behind the payout schedule shown at right is to offer the player five choices, one for every symbol that appears on the reels, and, while largely retaining the conventional payout structure of an ordinary slot machine, to still move to some extent in the direction of the Seven-Way Multi-Bell in that when the player chooses one of the five symbols on which to bet, a prize, although small, will be won even if that symbol only comes up on the first reel.
Aside from questions of implementation, however, there is another reason to doubt whether such a payout schedule is even possible.
Except for the very earliest payout schedules, where the prizes were relatively small, and there were no jackpots, it was necessary to decrease how often winning combinations came up by skewing the distribution of symbols on the wheels; so instead of having, say, five oranges and four plums on each of the first two reels, one might have eight oranges and one plum on the first reel, and two oranges and seven plums on the second reel.
But for a payout schedule like the one shown at right to make sense, it would seem that a relatively even distribution of symbols on the reels is required, making it impossible for a profitable arrangement to be constructed. And, indeed, I tried that, and it definitely did not work. Perhaps, though, the distribution of symbols could be made uneven in such a way that the additional payout for each chosen symbol is equal.
Let's see what would happen for one possible arrangement:
(%) Cherries 3 5 6 (O) Oranges 4 4 4 (@) Plums 4 4 3 (A) Bells 3 6 6 (=) Bars 6 1 1
For the basic payouts, clearly this distribution will be highly profitable:
Reel Combinations Value Amount
1 2 3 Paid
%%. 3 * 3 * 14 = 126 * 2 = 252
%%% 3 * 3 * 6 = 54 * 4 = 216
OOO, OO= 6 * 5 * 4 = 120 * 10 = 1200
@@@, @@= 3 * 5 * 5 = 75 * 14 = 1050
AAA, AA= 2 * 6 * 7 = 84 * 18 = 1512
=== 6 * 1 * 1 = 6 * 50 = 300
----
4530
The remaining number of coins is 3470, so that is the limit for any of the additional payouts.
Reel Combinations Value Amount
1 2 3 Paid
Cherries:
%.. 3 * 17 * 20 = 1020 * 3 = 3060
%%. 3 * 3 * 14 = 126 * +3 = 378
%%% 3 * 3 * 6 = 54 * +4 = 216
----
3654
Oranges:
O.. 6 * 15 * 20 = 1800 * 2 = 3600
OO. 6 * 5 * 15 = 480 * 5 = 2400
OOO, OO= 6 * 5 * 5 = 120 * +10 = 1200
----
6400
Plums:
@.. 4 * 15 * 20 = 1200 * 2 = 2400
@@. 4 * 5 * 15 = 300 * 7 = 2100
@@@, @@= 4 * 5 * 5 = 100 * +14 = 1400
----
5900
Bells:
A.. 4 * 16 * 20 = 1280 * 2 = 2560
AA. 4 * 4 * 13 = 208 * 9 = 1872
AAA, AA= 4 * 4 * 7 = 112 * +18 = 2016
----
6448
Bars:
=.. 1 * 19 * 20 = 380 * 3 = 1140
==. 1 * 1 * 19 = 19 * 10 = 190
=== 1 * 1 * 1 = 1 * +150 = 150
----
1480
If we change the payout in the case where cherries are chosen to 2 coins instead of 3 coins for a single cherry, we lower the additional payout by 1020 coins, from 3654 coins to 2634 coins, which allows that choice to be profitable.