Note: to supply some context, images of the slot machines mentioned, taken from old advertisements for them, have been included where possible. However, much clearer images, in full color even, are easily available with a quick web search if one is interested. |
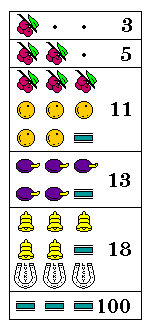
Some books on gambling illustrated the following as a typical slot machine arrangement:
(%) Cherries 5 7 3 (O) Oranges 4 1 10 (@) Plums 6 1 4 (A) Bells 1 9 1 (U) Horseshoes 2 1 1 (=) Bars 2 1 1
perhaps with payouts like these:
%.. 3 %%. 5 %%% 11 OOO, OO= 11 @@@, @@= 13 AAA, AA= 18 UUU 18 === 100
if it were, as I had recently come to suspect, a Jennings Standard Chief Bell or Jennings Export Chief, which indeed had those payouts.

This is a more modern arrangement, of the general style favored in the postwar era. Lemons are completely removed from the machine; instead, the horseshoe is added. Some accounts of this arrangement instead refer to the added symbol as a melon. Many modern machines have a second jackpot symbol; while earlier machines with a jackpot symbol other than the bar (and on some of them, three bars only won 20 coins rather than a jackpot) used a gold coin symbol for a "gold award", the melon, as well as a red number 7, were common added jackpot symbols, so I had originally expected three horseshoes to win a jackpot instead of just 18 coins.
And now even a single cherry on the first reel wins. Note, however, that there were many different payout arrangements used in the postwar era; no one arrangement was nearly universal, as was the case with the prewar era. And often, both pre-war and postware, even slot machines with the same model name had different reel strips and corresponding payout discs available for them.
The melon as an extra jackpot symbol appears to have been introduced by Mills on their Melon Bell machine; they've also used a 7 in this role instead. The melon was later also found on Bally and Sega machines.
Here, a greater effort has been taken to limit the number of times a winning combination occurs. There is only one bell on the first and third reels, so the second reel can safely have nine bells on it, and so there is only one orange, and one plum, on the second reel.
We can note that if every possible combination of the reels occurs exactly once in 8000 plays, then the machine takes in 8000 coins, it will give out the number of coins calculated as follows:
Reel Combinations Value Amount
1 2 3 Paid
5 * 13 * 20 = 1300 * 3 = 3900
5 * 7 * 17 = 595 * 5 = 2975
5 * 7 * 3 = 105 * 11 = 1155
4 * 1 * 11 = 44 * 11 = 484
6 * 1 * 5 = 30 * 13 = 390
1 * 9 * 2 = 18 * 18 = 324
2 * 1 * 1 = 2 * 18 = 36
2 * 1 * 1 = 2 * 100 = 200
----
9364
and, of course, this can't be right, and so that arrangement of symbols must belong to the reel strips of a machine with smaller payouts in some respect.
Changing the payout for one cherry to only two coins would reduce the total payout to 8064 coins, and so some additional changes, such as paying 3 coins for two cherries and 5 coins for three cherries would be enough to make the machine at least slightly profitable. As the book from which I learned of this machine mentioned the Jennings Lucky Bell was an earlier, almost identical machine, perhaps it was the one with this schedule of symbols, and lower payouts such as those.
And only a slight change would be needed to make the higher payouts profitable; one of the simplest would be to replace some of the cherries on the first reel by additional horseshoes.
So the basic idea behind a slot machine is that the chances of a winning combination are reduced by having very unequal numbers of symbols on the different wheels.
This particular arrangement resembles some used on Jennings slot machines known to me. For example, the V-12-70 set of reel strips, which does not include an extra jackpot symbol, has this arrangement:
(%) Cherries 3 7 3 (O) Oranges 7 1 10 (@) Plums 6 1 5 (A) Bells 1 10 1 (=) Bars 3 1 1
And their payouts would be:
Reel Combinations Value Amount
1 2 3 Paid
3 * 13 * 20 = 580 * 3 = 1740
3 * 7 * 17 = 357 * 5 = 1785
5 * 7 * 3 = 105 * 11 = 1155
7 * 1 * 11 = 77 * 11 = 847
6 * 1 * 6 = 36 * 13 = 468
1 * 10 * 2 = 20 * 18 = 360
3 * 1 * 1 = 3 * 100 = 300
----
6655
for a profit of 16.8125%.
And then there's V-12-88, which has this arrangement:
(%) Cherries 2 8 3 (O) Oranges 8 1 10 (@) Plums 6 3 5 (A) Bells 2 8 1 (=) Bars 2 1 1
This principle could be taken to extremes, as this example illustrates:
(*) Lemons 2 1 5 (%) Cherries 5 2 1 (O) Oranges 1 1 10 (@) Plums 1 5 2 (A) Bells 1 10 1 (=) Bars 10 1 1
With 20 symbols on each wheel, three of the same symbol, one on each reel, can only come up 10 times for any one symbol, for a total of 60 times for all six different symbols. So that could pay out a jackpot of 100 coins in each case, giving a total payout of 6000 coins out of 8000, or a payout percentage of 75%.
While there were actual slot machines with 9 or 10 occurences of the same symbol on one reel, that means that one often sees the same symbol twice among the three visible symbols on any given reel. If one were to restrict oneself to using any given symbol at most six times on a given reel, so that this need never occur, could one still design a machine that could be profitable paying only jackpots?
Since a 50 coin payout still counts as a jackpot, it is possible:
(O) Oranges 6 4 1 (@) Plums 1 6 4 (A) Bells 4 1 6 (=) Bars 6 1 2 (C) Melons 2 6 1 (7) Sevens 1 2 6
If three bars, three melons, and three sevens each paid 100, then each symbol would pay 1200 coins, since in each case three of that symbol could occur 12 times. Each of the first three symbols occurs three in a row twice as often, so if the payout were 50, half as much, then we have six symbols each paying 1200 coins, for a total payout of 7200 out of 8000, or 90%. Of course, a jackpot-only machine should really have a lower percentage than that, unlike one with many small payouts.
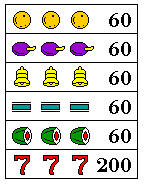
There have been actual slot machines made that only pay jackpots. Most of them have numerous blank positions on the reels, but in the book Slot Machines: A Pictorial History of the First 100 Years, there is pictured a Mills hi-top slot machine modified by the Nugget casino in Sparks, Nevada (not the Golden Nugget casino in Las Vegas) so that all the winning combinations paid jackpots without resorting to that expedient; its payout schedule is shown at right.
I don't know how the symbols were distributed on its reels, but one possibility might be something like this:
(O) Oranges 6 5 1 (@) Plums 1 6 3 (A) Bells 3 1 6 (=) Bars 6 1 3 (C) Melons 3 6 1 (7) Sevens 1 1 6
which would lead to the following payout:
6 * 5 * 1 = 30 * 60 = 1800
1 * 6 * 3 = 18 * 60 = 1080
3 * 1 * 6 = 18 * 60 = 1080
6 * 1 * 3 = 18 * 60 = 1080
3 * 6 * 1 = 18 * 60 = 1080
1 * 1 * 6 = 6 * 200 = 1200
----
7320
which would lead to a house advantage of 8.5%; just by allowing up to 7 of the same symbol on a reel, so that the same symbol would occasionally be visible twice, that could easily be considerably increased:
7 * 3 * 1 = 21 * 60 = 1260
1 * 7 * 2 = 14 * 60 = 840
2 * 1 * 7 = 14 * 60 = 840
7 * 1 * 2 = 14 * 60 = 840
2 * 7 * 1 = 14 * 60 = 840
1 * 1 * 7 = 7 * 200 = 1400
----
5020
for a house percentage of 37.25%.
The following diagram shows
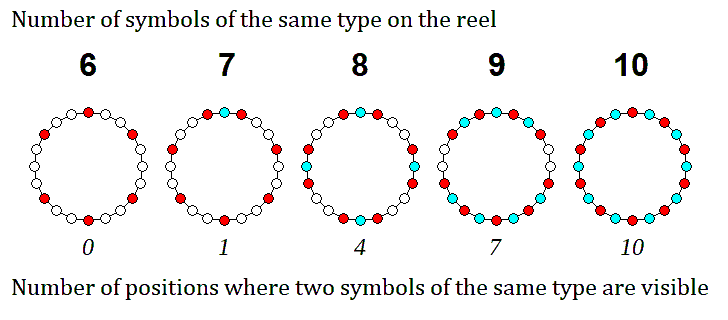
how, as the number of times that we want the same symbol to appear on a reel with 20 positions increases, if we try to keep them as evenly spaced as possible, the number of positions in which two of the same symbol are visible in a normal 3-line window will increase. (Of course, the circles filled with red represent the locations of the symbol that is being repeated, and the circles filled with light blue-green are the locations which, when they come up on the center line, will be flanked by two of that symbol, one above and one below.)
As for those with blank positions on the reels, sometimes they had positions that were actually blank, as on the Seeburg 3-Line Stars and Bars and many others, and in at least one case, a Pace Deluxe Cherry Bell, which closely resembles the Pace Comet, modified by another casino, the Harrah's Club casino, had each reel bearing one word from the phrase "Pays Jackpots Only" in the positions that would not form part of any prize.