The theory of probability is an entertaining branch of mathematics that has occasionally been the subject of controversy.
In the beginning, the notion of probability was considered by some to be impious; everything that could either happen, or fail to happen, will do so in accordance with God's will, and thus the concept of probability is meaningless.
And, of course, the clearest classical illustrations of probability are associated with the disreputable activity of gambling.
But other controversies are also associated with probability. Bayesian statistics are a recent invention whose validity is controversial.
What are Bayesian statistics?
In classical probability, one starts with assumed probabilities: a die has six identical sides, and so we assume that an ideal die has an equal probability to have any of its six faces uppermost after being thrown. From that, we can then draw conclusions about the chances of various combinations of dice being thrown.
Bayesian statistics, instead, deal with inferring probabilities by induction. If we observe an event happening on the average one time out of every ten, we can conclude that its actual probability of happening is most likely one time out of ten, and, depending on how many observations we have made, we can also talk about the probability that the real probability is higher or lower than the observed value.
But in a physical system, an actual probability of an event happening already exists, and all that can happen is that during a series of observations, one might, with a certain probability, see more or fewer occurences of that event than are more likely. In a sense, this simply takes the original objection to probability, based on a deterministic universe, to the next higher level.
The response, of course, is that just as the roll of a die is deterministic if we could know the state of every atom in the air through which the die is thrown, and the brain and body of the thrower, actual probabilities of events are things we may either know or be ignorant about, and in the absence of an opportunity to obtain knowledge of a priori probabilities in a reductionist fashion, by breaking down a system into its component parts, each of which are simple enough to fully understand, observation of behavior is another method to obtain information.
The tragedy of the Space Shuttle Columbia provided an illustration of the meaning of Bayesian statistics. In a news report after that tragedy, Jesco von Putkammer was interviewed by a reporter, and he denied that the tragedy meant that the Space Shuttle was necessarily unsafe. In effect, he noted that if the chance of a fatal accident with the Space Shuttle were one in a million, that would not prevent the accident from taking place on the 25th flight, as it did, instead of the 1,000,000th flight, or the 500,000th flight.
And that is absolutely true, yet it is also reasonable, in the absence of other information, to conclude that the likeliest value for the risk is on the order of one in fifty, even if that value is itself highly uncertain.
Much of classical probability theory would seem to be nothing more than an exercise in simple arithmetic.
Thus, although it is complicated, there seems to be nothing profound about calculating the odds for a slot machine or one-armed bandit. This is a gambling device that has three reels, each with 20 symbols on it, these symbols often being chosen from a set of six or seven different symbols.
One example of the assortment of symbols that can appear on a slot machine is:
(*) Lemons 3 - 4 (%) Cherries 7 7 - (O) Oranges 3 6 7 (@) Plums 5 1 5 (A) Bells 1 3 3 (=) Bars 1 3 1
which is designed for a machine with the following schedule of payouts:
%%. 3 %%*, %%A 5 OOO, OO= 10 @@@, @@= 14 AAA, AA= 18 === 120
This payout schedule is one of those illustrated below.
A large number of slot machines made prior to World War II by many manufacturers had the schedule of payments shown above, except that the combination of three bars paid out 20 coins plus the jackpot, whatever it might be; for purposes of a simple calculation, a fixed jackpot of 100 coins is assumed.
The number of times the various combinations of symbols would occur, on average, if the machine were operated 8000 times can be calculated in a straightforwards manner, and these probabilities (scaled up by a factor of 8000, the total number of combinations) can then be multiplied by the amount paid for the combination to work out how profitable the machine is:
Reel Combinations Value Amount
1 2 3 Paid
7 * 7 * 13 = 637 * 3 = 1911
7 * 7 * 7 = 243 * 5 = 1215
3 * 6 * 8 = 144 * 10 = 1440
5 * 1 * 6 = 30 * 14 = 420
1 * 3 * 4 = 12 * 20 = 240
1 * 3 * 1 = 3 * 120 = 360
----
5586
for a profit of 30.175%. Thus, in the first line, the calculation is based on the fact that there are seven cherry symbols on the first reel, seven cherry symbols on the second reel, and thirteen symbols that are neither a lemon nor a bell on the third reel.
More about the fascinating world of slot machines continues on this page.
The study of probability as a mathematical discipline can be said to have its start in a question concerning the throw of three dice. A mathematician was asked why it should be likelier to throw 10 with three dice than to throw 9. Each combination can be made in six ways:
9 can be made as 1-2-6, 1-3-5, 1-4-4, 2-2-5, 2-3-4, 3-3-3;
10 can be made as 1-3-6, 1-4-5, 2-2-6, 2-3-5, 2-4-4, 3-3-4.
Although there are 56 visibly different combinations that can be thrown with three identical dice, assuming that each one is equally likely is a mistake. Realizing this is what began the journey to making probability a science.
It is reasonable to assume that one die is equally likely to come up with any one of its six faces. Starting with what we do know, instead of guessing what three dice might do, to break down their behavior into a combination of the behaviors of three dice, one thinks of three dice that differ in color, or which are thrown in three separate dice cages.
This then leads to the conclusion that instead of 56 equally probable outcomes, there are 216 possibilities equal in likelihood. A combination where all three dice come up with the same number, such as 3-3-3, reflects only one of those possibilities, but one where all three dice are different, such as 2-3-4, reflects six of them. When two of the dice show the same number, and the third one is different, three of the 216 possibilities are involved.
Thus, the chance of throwing a 9 is 6+6+3+3+6+1 or 25 out of 216, while the chance of throwing a 10 is 6+6+3+6+3+3 or 27 out of 216.
The odds of throwing different totals with three dice approximates a bell curve or normal distribution, and this has made the use of three dice popular for determining traits in role-playing games:
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 3 6 10 15 21 25 27 27 25 21 15 10 6 3 1
Most people are familiar with the game of Craps.
In this game, the player throwing a pair of dice wins if he throws 7 or 11 on his first throw, but loses if he throws 2, 3, or 12 on his first throw. If he throws another number, then he continues to throw the dice until he either throws that number again and wins, or he throws a 7 and loses.
The chance of throwing each of the possible numbers from 2 to 12 with two dice follows a triangular distribution:
2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 5 4 3 2 1
and the chance that the player throwing the dice will win can be determined by looking at the thirty-six possibilities for the first throw and their consequences:
2 is thrown 1 time, and leads to a chance to win of 0 3 is thrown 2 times, and leads to a chance to win of 0 4 is thrown 3 times, and leads to a chance to win of 3/9 5 is thrown 4 times, and leads to a chance to win of 4/10 6 is thrown 5 times, and leads to a chance to win of 5/11 7 is thrown 6 times, and leads to a chance to win of 1 8 is thrown 5 times, and leads to a chance to win of 5/11 9 is thrown 4 times, and leads to a chance to win of 4/10 10 is thrown 3 times, and leads to a chance to win of 3/9 11 is thrown 2 times, and leads to a chance to win of 1 12 is thrown 1 time, and leads to a chance to win of 0
The reason the chance to win is 3/9 when 4 is thrown is because there are 3 ways to throw a 4, 6 ways to throw a 7, and only those two throws count, and the first one is decisive, afterwards.
The chance to win, therefore, is:
1 3 2 2 5 5 1 1 - * - + - * - + -- * -- + - + -- 6 9 9 5 18 11 6 18
which works out to 244/495, or 49.292929... percent.
This might seem complicated enough. But the game of Craps is a simplified descendant of the game of Hazard.
In the original form of the game of Hazard, the two dice are thrown first to establish the main point; this can only be 5, 6, 7, 8 or 9, and they are thrown again until such a number is obtained.
Then, they are thrown once to obtain a chance point; this can be 4, 5, 6, 7, 8, 9, or 10. If, on that throw, the main point is thrown again, the caster wins. As for the throws of 2, 3, 11, and 12, their significance depends on what the main point is:
If the main point is: Wins Loses 5 or 9 2, 3, 11, 12 6 or 8 12 2, 3, 11 7 11 2, 3, 12
When the main point is 7, which it will be 6 times out of 24 (or 1 time out of 4), one obtains the same probabilities of winning as in the modern game of Craps.
When the main point is 6, the chances of winning are as follows:
2 is thrown 1 time, and leads to a chance to win of 0 3 is thrown 2 times, and leads to a chance to win of 0 4 is thrown 3 times, and leads to a chance to win of 3/8 5 is thrown 4 times, and leads to a chance to win of 4/9 6 is thrown 5 times, and leads to a chance to win of 1 7 is thrown 6 times, and leads to a chance to win of 6/11 8 is thrown 5 times, and leads to a chance to win of 5/10 9 is thrown 4 times, and leads to a chance to win of 4/9 10 is thrown 3 times, and leads to a chance to win of 3/8 11 is thrown 2 times, and leads to a chance to win of 0 12 is thrown 1 time, and leads to a chance to win of 1
and the chance of winning is the same when the main point is 8; the roles of the throws of 6 and 8 are interchanged, but as their likelihood is identical, the overall chance is the same.
The chance of the main point being either 6 or 8 is 10 times out of 24 (or 5 times out of 12). When the main point is either 6 or 8, the caster's chance of winning is 6961/14256, or 48.82856341189674523007856341189674523007856... percent.
When the main point is 5, the chances of winning are as follows:
2 is thrown 1 time, and leads to a chance to win of 0 3 is thrown 2 times, and leads to a chance to win of 0 4 is thrown 3 times, and leads to a chance to win of 3/7 5 is thrown 4 times, and leads to a chance to win of 1 6 is thrown 5 times, and leads to a chance to win of 5/9 7 is thrown 6 times, and leads to a chance to win of 6/10 8 is thrown 5 times, and leads to a chance to win of 5/9 9 is thrown 4 times, and leads to a chance to win of 4/8 10 is thrown 3 times, and leads to a chance to win of 3/7 11 is thrown 2 times, and leads to a chance to win of 0 12 is thrown 1 time, and leads to a chance to win of 0
and the chance of winning is the same when the main point is 9; the roles of the throws of 5 and 9 are interchanged, but as their likelihood is identical, the overall chance is the same.
The chance of the main point being either 5 or 9 is 8 times out of 24 (or 1 time out of 3). When the main point is either 5 or 9, the caster's chance of winning is 1396/2835, or 49.241622574955908289241622574955908289... percent.
Given the probabilities of the different main points, the caster's chance of winning in the original form of the game of Hazard is 1979/4032, or 49.0823412698412698... percent.
As the probabilities of winning for each of the possible values of the main point are so nicely balanced, to speed things up, the rule was changed so that instead of first rolling the dice until a main point was obtained, the caster could simply choose, and announce, his own main point before throwing for the chance point.
Since the caster's chance of winning was 49.29% for a main point of 7, 49.24% for a main point of 5 or 9, and 48.83% for a main point of 6 or 8, 7 was the caster's best choice, which led to the modified game of Hazard quickly changing to the modern game of Craps.
In the form of Craps played in a casino, Bank Craps, people can also bet against the player throwing the dice; so that this bet is also profitable for the casino, the most common rule is that if the caster loses by throwing a 2 on the first throw, a bet against the caster is not lost, but does not win either. This makes the house percentage on a bet against the caster only slightly less than that on a bet for the caster. Some Bank Craps layouts instead bar 3, making the percentage on a bet against the caster considerably higher; others offer bettors a choice of betting against the caster with 2 barred, or of betting against the caster with 12 barred; this provides a small additional reassurance of fair play.
In Hazard, since the caster's chance of winning is significantly smaller for a main point of 6 or 8, if 2 were barred on a bet against the caster, although the house would have an advantage, it would be only 0.435 percent, between a quarter and a third of that for the other bets with or against the caster; thus, either 3 or 11 (which is a losing throw when 6 or 8 is the main point, 12 in this case being a winning throw) would more likely be barred were there such a thing as Bank Hazard.
And if there were, the betting layout might look like this:

The Big 6 and Big 8, and 4, 6, 8 and 10 the hard way would always be rolled against 7, as in Craps, so the odds of these bets would remain the same; even money for the Big 6 and Big 8, 7 to 1 (or 8 for 1) for 4 and 10 the hard way, 9 to 1 (or 10 for 1) for 5 and 9 the hard way.
The layout is shown here with odds that give a lower house percentage than is usual on a few bets. Thus, a field bet pays triple, rather than double, if 2 is rolled, and bets on 2 or 12 pay 31 to 1 (or 32 for 1).
The rule of play for Bank Hazard that is envisaged as being applicable to this layout is that the shooter may announce his main point, whether 5, 6, 7, 8, or 9, and may also announce "Roll for Main" or just "Main" to indicate that his main point will be decided by the dice; if no announcement is made, the main point is 7 by default; thus, unless a main point is specified, play proceeds as at Craps.
The shooter may also announce "Wrong" or "To Lose" or "Miseré" in addition to his point; in that case, he retains control of the dice if he throws a losing combination, including one that is barred (one that neither wins nor loses for wrong bettors) and loses control of the dice if he throws a winning combination. This does not affect which dice rolls win for bettors on the Pass Line and the Don't Pass line, thus, in that case, bettors who believe the shooter is "on a roll" would bet on the Don't Pass line in order to win.
Furthermore, when the shooter is rolling for a main point, instead of rolling the dice indefinitely until a number from 5 through 9 is thrown, it would seem appropriate for the rules to provide that a throw of 2, 3, 4, 10, 11, or 12 when rolling for the main point would make the default value of 7 the main point. This way, the main point is always decided by a single throw of the dice, removing what was perhaps the single biggest reason that Hazard was displaced by Craps.
The rolls which lose or win immediately on the throw for the Chance point are given above in the rules for Hazard.
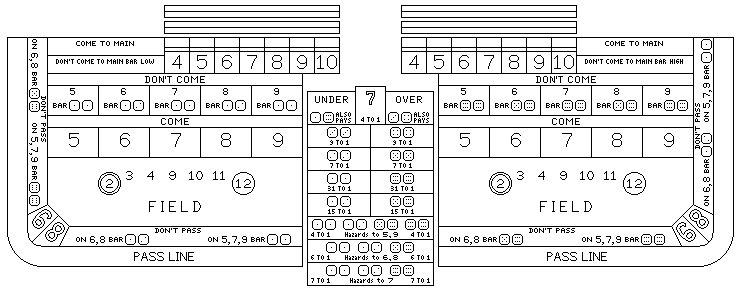
The fact that each of the "Come" and "Don't Come" lines on the layout are divided into five areas, the feature which most strongly distinguishes it from a Bank Craps layout, gives the Come and Don't Come bettor the same freedom as the shooter to chose a point. Bets placed on the "Come to Main" and "Don't Come to Main" are moved to the appropriate space on the Come or Don't Come line below them when a roll from 5 to 7 decides the main point applicable to them.
Note that the Place bets on the layout include the number 7, unlike those on a Bank Craps layout. The meaning of these bets, therefore, is determined by the current main point of the shooter, and bets cannot be placed on the space corresponding to that point, which is covered by a marker. Since a bet can be placed on chance points other than the shooter's chance point, if the shooter wins, it is possible that a bet might be undecided at that time, and the shooter can call a different main point for his next throw (or the point can change if he is remaining with "Roll for Main"); hence, there are two rows above the place area to which bets can be moved that remain associated with a different main point no longer in use, that point being indicated by a marker of appropriate size.
The odds for the place bets are:
Main Point is 7 Main Point is 6 or 8 Main Point is 5 or 9
True Normal Normal True Normal Normal True Normal Normal
Wrong Wrong Wrong
4,10 2 to 1 9 to 5 5 to 11 5 to 3 6 to 4 2 to 4 4 to 3 5 to 4 2 to 3
5,9 3 to 2 7 to 5 3 to 5 5 to 4 6 to 5 3 to 6 1 to 1 11 to 12 11 to 12
6,8 6 to 5 7 to 6 4 to 5 1 to 1 11 to 12 11 to 12 4 to 5 3 to 4 6 to 5
7 -- -- -- 5 to 6 4 to 5 7 to 6 2 to 3 7 to 5 3 to 5
A place bet or don't place bet at true odds may be made up to what one has wagered on the pass line or the don't pass line.
The spaces for Under and Over 7 are restored to the layout, but they are modified so that Under 7 also pays when 7 is rolled as 1-6, and Over 7 also pays when 7 is rolled as 3-4, so that the percentage on those spaces is reduced to 5 5/9%. Also, in addition to a space for betting on 2, 3, and 12, the three combinations which are craps when 7 is the main point, spaces are provided for betting on 2, 3, and 11, the three combinations which are craps when 6 or 8 is the main point, and for betting on 2, 3, 11, and 12, all four of which are craps when 5 or 9 is the main point.
Many books on gambling will note that, in an American casino, a bet for the caster at Craps carries a house percentage of 1.414% against it, while a bet on a single number at Roulette, on the American layout with two zeroes, carries a house percentage of 5.263% against it, as does a bet on red or black, since American roulette does not have the prison rule of European Roulette, with one zero, which reduces the percentage against these bets to half that against that of other bets on the layout.
It is quite correct, therefore, that a bet on the line at Craps would be a better bet than a bet on red or black, or odd or even, or high or low, in an American-style casino.
But let us suppose one has a single chip in one's hand, and one's intent is to gamble it so as to win about 30 times its value if one is lucky.
One can bet it on a single number at Roulette, and one's average return will be 5.263% less than the chip's value, although what will actually happen is that one will either lose it, or win 36 times its value. Or one can let it ride five times in a row at Craps, to either lose it, or win 32 times its value; then, one faces a percentage of 6.8735% against one.
To compare different bets offered in a casino in a useful manner, as instruments towards a goal of winning one's stake times a given amount, a game with a probabity p of winning n times one's stake can be considered as equivalent to a game with a probability p^(log(N)/log(n)) of winning N times one's stake, and different games should be compared with a constant N. How to apply this rule to games with multiple different payouts, such as playing the field in Craps, or gambling with a slot machine, however, is less obvious; presumably, the best way is to divide the input stake between the possible payouts in such a way that the normalized expectation for each one is identical.
If one wishes to talk about mathematics and gambling, another item of interest is the arrangement of numbers on the roulette wheel:

the diagram above shows how the numbers on the European and American roulette wheels are arranged to allow red and black, high and low, even and odd, the three dozens and the three columns all, simultaneously, to come close to alternating.
The numbers are shown as they are typically printed on the wheel; on the European single-zero wheel, the numbers are printed with their tops facing out, and their bottoms towards the center, and thus the numbers are shown in clockwise order; on the American double-zero wheel, the numbers are printed with their bottoms facing out, and their tops towards the center, and thus the numbers are shown in counter-clockwise order. Here is a picture similar to a common one, showing the European and American roulette wheels side by side:

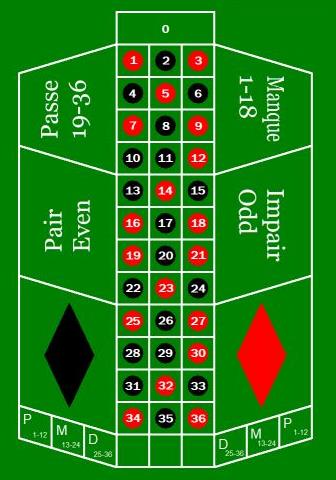
Another common diagram, which I have also drawn myself, illustrates the roulette layout; the European single-zero form is shown. This is useful for clearly understanding which numbers are red, and which numbers are black, and why.
One old French book (Nouvelle Marche Irrégulière sur le Jeu de la Roulette) showed a diagram of a roulette wheel with both 0 and 00 which had the other numbers arranged as in the current European single-zero roulette wheel, except that instead of the sequence being 26 0 32 15 19... it started off 26 32 15 0 19... with the zero advanced two places, and thus the double-zero was between 5 and 24. (However, the tops of the numbers were facing to the center of the wheel, so the numbers went around counter-clockwise, as on the American double-zero roulette wheel.)
Also, in Macao, the roulette wheels have a single zero, but the sequence of numbers is the same as that of the American roulette wheel. The single zero is in the position that the double-zero, 00, has on the American wheel. The numbers are printed with their tops facing outwards, so the natural reading direction is clockwise; the numbers proceed, therefore, clockwise, from the 0 in the same order as they proceed counter-clockwise from the 00 on the American roulette wheel.
Thus, the roulette wheel in Macao follows the same clockwise convention as a European roulette wheel, but with the numbers in the order 0 27 10 25 29... .
The following diagram
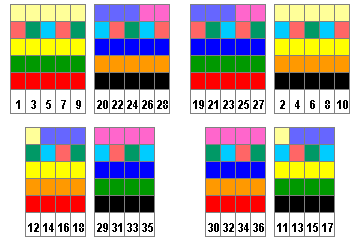
illustrates the difficulties faced in making an improved order of numbers for roulette wheels. In the first half of the top row, we see ten numbers consisting of five that are red, odd, and low, and five that are black, even, and high.
Alternating numbers from those two groups, to give a stretch of ten numbers that alternate from red to black, from odd to even, and from low to high, while it could lead to a good mixture of the numbers from the three columns, would lead to the result containing five numbers from the first dozen, three numbers from the second dozen, and two numbers from the third dozen.
If priority is given, as on the European roulette wheel, to the alternation from low to high over that from odd to even, the eight numbers in the first half of the bottom row that consist of four that are red, even, and low, and four that are black, odd, and high will complement this first group in respect of the distribution of the three dozens.
The following diagram shows one possible improved ordering for the numbers on the roulette wheel in the top row:

the second row shows an early French arrangement of the numbers on the roulette wheel that appears in at least one old engraving of a roulette wheel and layout (with tops facing out, hence in clockwise order), and the third row shows an arrangement that appeared in many old books on the rules of various games. I have also seen an illustration in an old book where that arrangement of numbers is used with 0, 00, and Eagle (for triple zero), where the Eagle is added immediately adjacent to, and preceding, the 00. (This arrangement also has the tops facing out, and thus goes around the wheel clockwise.) The wheel and layout from that old illustration are shown below:
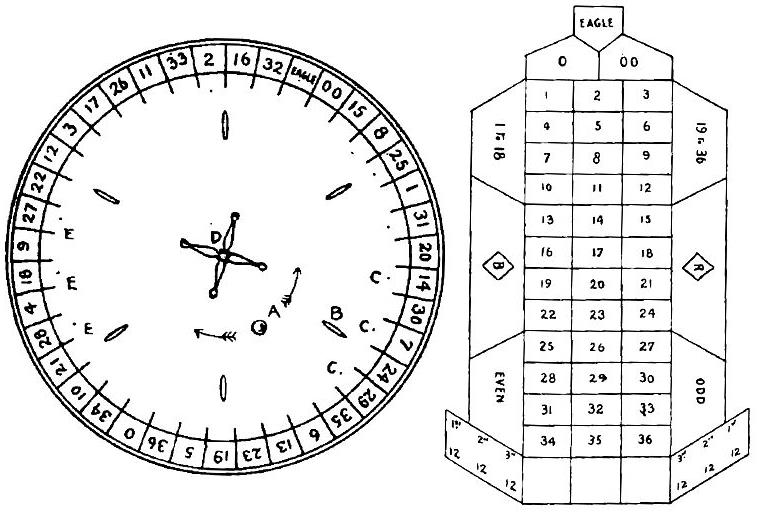

The fourth row shows an arrangement used in a coin-operated gambling device from 1936, Roll-Ette from the H. C. Evans company. It was called Ro-Bo-Lette instead in an advertisement announcing that it would be presented at the 1936 Coin Machine Show, and it was called Rou-Lette instead in an early advertising flyer that included a picture of the machine. A picture of one is shown at right. Interestingly enough, they had previously made roulette wheels with the standard arrangement. As the way it was designed allowed a player to place a bet on one number in each of the three columns, I looked to see if there was any particular property in the second row of colored blocks, indicating which columns the numbers belong to, but I did not notice one. Note that while the colors do not alternate, the size of clumps of any one color is still limited. (The feet of the numbers face out, so they go around the wheel counter-clockwise.)
The Evans Roll-Ette sold, originally, for $262.50 in 1936, making it considerably more expensive than smaller-sized slot machines. Used machines were still being sold in 1946, for $89.50 by the Milwaukee Coin Machine Company, for example. In 2006, one sold for $12,500 at auction, and in 2015, another one sold for over $56,000, as it is now one of the rarest and most sought after coin machines.
In the three historical arrangements shown, as opposed to my attempt at an improved arrangement, the numbers that are red and black do not alternate.
I would be inclined to suspect that what had been the case for roulette wheels laid out according to these two older arrangments is that the numbers on the wheel still did alternate between red and black, since bets on the red and black colors were still provided for both of them, according to the sources for those wheel arrangements, but which numbers were red, and which numbers are black, differed from the modern case.
However, the old engraving of a roulette wheel and layout shows a layout similar to the modern one, with the numbers arranged in three columns. If red and black numbers did alternate on the wheel, one would also expect that red and black numbers would appear on the layout in some symmetric fashion, even if it was a different one from that used today.
3 6 9 12 15 18 21 24 27 30 33 36
-- -- -- -- --
2 5 8 11 14 17 20 23 26 29 32 35
-- -- -- -- -- -- --
1 4 7 10 13 16 19 22 25 28 31 34
-- -- -- -- -- --
Instead, we find a messy and unbalanced arrangement.
In the case of the alternative arrangement of the roulette wheel shown in some game books, since there is both a 0 and a 00, the alternation of red and black would be independent in each half, allowing some freedom in choosing an arrangement:
3 6 9 12 15 18 21 24 27 30 33 36 A D A B D B A C B C C C 2 5 8 11 14 17 20 23 26 29 32 35 B D D B D B C D A D B C 1 4 7 10 13 16 19 22 25 28 31 34 C B D B C A C A D B D A
That is, if A is red, and B is black, C could be red, and D could be black, or those two letters could be the other way around, with D red and C black.
While there are stretches that suggest some sort of alternation, it still doesn't seem that either way of assigning the colors works particularly well, although making D and C respectively similar to A and B helps to create larger patches that are checkerboard-like instead of solidly colored.
The earliest roulette wheels in France, like those currently in use in United States casinos, had both a zero and a double-zero. However, some sources note that instead of being green, 0 was red - and it was considered to be odd and low as well; and 00 was black - and it was considered to be even and high as well.
This did not mean that the even-money bets gave the house no percentage; if a zero or double-zero won for such a bet, it neither lost nor won; thus, for those bets, it was as if the wheel only had one zero instead of two.
This, I think, explains why the modern European single-zero roulette game includes the prison rule; when the single-zero roulette wheel was introduced in 1843 by Louis and François Blanc at Bad Homburg, in order to be accepted as a true improvement on the existing double-zero roulette wheels, it needed to cut the percentage in half on all the bets, including the even-money bets, which, at the time, had a house advantage as if only one zero were present on those double-zero wheels.
The prison rule in European roulette is this: when zero comes up, the even-money bets, instead of being lost outright, are moved to an area within the spaces on which they are placed, called the prison, and then on the next spin, either they are lost, or, if this time they win, then they are simply returned (to the main area of the same space of the layout on which they were placed, from which the player may retrieve them) without additional winnings; once again, the same thing as is called "no action" in Craps.
Later on, since coloring 0 red and 00 black caused confusion and complaints, those numbers were colored green instead, and both zeroes simply lost on the even money bets as is the case today with the 38-number wheel.
The old French arrangement from one engraving, although it did not alternate the colors, turns out to have large areas of similarity with the arrangement of numbers on the American roulette wheel with 0 and 00.
Old French
0 11 24 30
*
23 4 14 33 2
-- -- * --
6 18 31 19 8 12 29 25 10 27
-- -- -- -- -- -- -- -- -- --
1 13
-- --
34 16 21 35 3
* * * *
22 5 15 32 20 7 17 36 26 9 28
-- -- * -- -- -- * * -- -- --
American
0 2 14 35
23 4 16 33 21
-- -- --
6 18 31 19 8 12 29 25 10 27
-- -- -- -- -- -- -- -- -- --
00
1 13
-- --
36 24 3 15 34
22 5 17 32 20 7 11 30 26 9 28
-- -- -- -- -- -- -- --
In addition to the matching numbers being underlined in both lists, the numbers that do not match in the old French arrangement, but which are still of the correct alternating color for their position are marked with an asterisk.
Of course, the Old French arrangement goes around the wheel clockwise, while the American one goes around the wheel counter-clockwise, so from that point of view more than just a few numbers are changed.
Retaining the modern arrangement of red and black numbers on the layout, if it is felt desirable to have a different sequence of numbers for Roulette with three zeroes, one could take the third arrangement in the illustration as a basis by referring to its red and black numbers alternately, leading to this sequence:
0 34 10 21 28 18 4 9 22 27 17 12 26 E 3 11 16 33 32 2 25 15 1 8 14 31 00 30 20 7 24 23 29 19 35 5 6 36 13
but that leads to several adjacent pairs of consecutive numbers, 33 and 32, 31 and 30, 24 and 23, and 5 and 6, so further rearrangement would be needed.
Alternation of the major bets on the roulette layout, however, is not the only characteristic that an arrangement of numbers on the wheel should satisfy. Various bets on three, four, or six numbers are possible on the roulette layout as well. In order to ensure that the numbers involved in any such wager are widely distributed on the wheel, it is sufficient to ensure that the numbers in any two consecutive rows of the layout are widely distributed. The following diagram:

illustrates how the arrangements considered above fare in this respect.

I have now encountered an image online of a very old French roulette wheel with a nonstandard layout, but not the same as the very old one I saw in a drawing. The arrangement has a strong resemblence to that on an American roulette wheel, and it goes as follows:
0 2 14 35 23 4 16 33 21 6 17 31 18
7 34 28 25 10 36 13 27 5 12 3 24
17 15 22 1 32 20 7 11 30 26 9 28
Red and black alternate most of the way around the wheel, with 0 green, as usual. However, not only are both 28 and 2 black, but as well both 5 and 12 are black.
Thus, the series of numbers around the wheel, except for the zero, consists of two sequences with an odd number of numbers in them, one from 2 to 5, and the other from 12 to 28, which both begin and end with a black number. So the wheel has 17 red numbers and 19 black numbers, which means that while red and black can still be used to make the layout look pretty, it would not be possible to let people bet on the colors!
Incidentally, like a typical French roulette wheel, the numbers had their bottoms towards the center of the wheel.
The numbers from 32 to 8, including the zero, are in the same sequence as on an American roulette wheel, except for being in reverse order. (However, as the numbers face the opposite way, they're in the same positions on the wheel.)
Then, 34 replaces 12.
And then the sequence continues, with the numbers 29, 25, and 10 matching the American roulette wheel.
Also, 17 is red instead of black, 5 and 12 are black instead of red, and 22 is red and 1 is black instead of the other way around.
I've put an image of how the roulette layout looks with these numbers changed in color over to the right of this description of that roulette wheel: the layout appears to completely lose the symmetry it formerly had.
While the Roulette wheel with both a 0 and a 00 originated in France, even back when it was common there, a higher percentage was taken on Roulette wheels in the United States, at least some of the time.
Several old books on games pictured an American roulette game where the wheel had the numbers from 1 to 28 instead of 1 to 36, and in addition to 0 and 00, a third zero was present, represented by the image of an Eagle.
These books showed the following arrangement of numbers on those wheels:
E 20 11 18 13 16 27 2 25 0 4 23 6 21 8 19 10 17 00 12 15 14 1 28 3 20 5 24 7 22 9
in a diagram like that shown on the right side of the image below, with the picture of the wheel shown enlarged on the left.
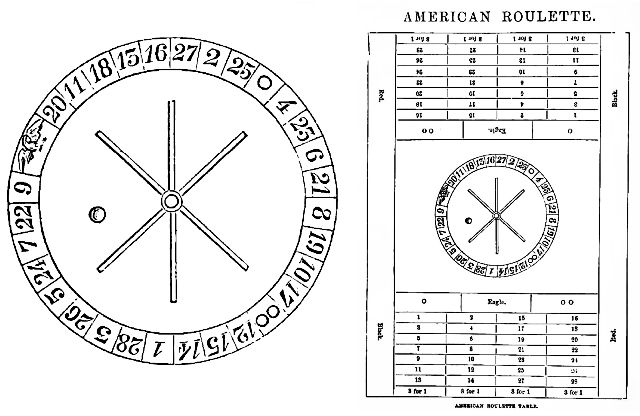
Spaces on the layout are also shown for betting on red or black, but not for the other even-money bets. The numbers from 1 to 28 are organized in four columns, and a bet on a single column is also possible. (The numbers on the wheel are shown with their tops facing out, thus are given in clockwise order.)
Which of those numbers are red, and which are black, though, is something at which I could only guess. However, recently I saw a photograph of a roulette wheel of this general type which was offered at auction. But it had a different arrangement of numbers on it:
E 16 3 12 21 4 25 8 17 22
R B R B R B R B R
0 14 7 26 15 10 19 2 23 6 27
R B R B R B R B R B
00 13 20 9 28 11 18 5 24 1
B R B R B R B R B
thus, the three zeroes are spaced as equally as is possible, the 0 is flanked by two red numbers, and the 00 is flanked by two black numbers. (This wheel had the bottoms of the numbers facing outward, so the numbers proceeded counter-clockwise around the wheel.)
And so all the odd numbers are black and all the red numbers are even on this wheel, which explains at least why there are no Even or Odd bets on the layout, if not the absence of High and Low bets.
Odd and even numbers also strictly alternate in the arrangement shown for 31-number wheels in the game books, except that in that arrangement the 0 and 00 are also flanked by one odd and one even number, like the Eagle, and so it is very likely that the same convention applied to them.
The overhead costs of having a croupier, heating and lighting, security, and so on, are constant, while the stakes players wager may be large or small. Thus, the games in a casino with lower percentages may have a higher minimum bet, with games having higher percentages having lower minimum bets.
In the case of roulette and games similar to it, this contrast is clearer than in most other cases.
An interesting intermediate form of Roulette is Roulca, originated at the Baden-Baden casino, and still chiefly played there.
The Roulca wheel has 25 compartments. One, called "Carteuni", bears on it a symble consisting of the four card suits in a vertical column, in the order Heart, Club, Diamond and Spade: this symbol plays the role of the zero.
The Roulca layout is similar to that for Roulette. On the side are large spaces - to the left, Low (lit. Second Half), Even, and Black; to the right, High (lit. First Half), Odd, and Red. Below the large spaces are four small spaces to bet on the four suits; from the outside in, Spade, Diamond, Club, and Heart.
As on the roulette layout, there are three columns of spaces for betting on individual cards, and below them there are three spaces for betting on the columns.
The spaces for cards are laid out in this order:
AH KC QD JS 10H 9C KD QS JH 10C 9D AS QH JC 10D 9S KH AC JD 10S 9H QC AD KS
As it is played in a German-speaking area, the Queen is noted by D (Dame) and the Jack is noted by B (Bauer).
As best I can make out, the order of the cards on the wheel seems to be:
(0) JD AC JH 9S AH KS 9D JS 9H JC AD KC QH 10S QD 10C 10H QC 10D QS KH AS KD 9C
Making use of the fact the cards were of the North German pattern was of significant assistance in interpreting the image. I read the cards from the wheel in a clockwise direction.
However, a Super Roulca slot machine shows this order of cards around the wheel, also read clockwise:
(0) JD KS AH QC KD 10S KH JC 10D QS 9H AC QD 9S 10H KC AD JS 9D 10C QH AS JH 9C
I had noticed that some online casinos offer a game called "Roulette 24", involving a wheel with numbers like the normal roulette wheel, but with 25 spaces and one zero like the wheel for Roulca. I had not thought that important enough to mention, but I recently came across a search result indicating that this game is also used in real brick-and-mortar casinos in Luxemburg.
This is the order of numbers on the wheel I've seen online, as it is consistent, perhaps it is also the real one used in Luxemburg:
0 15 19 4 21 2 9 22 16 11 3 6 1 8 23 10 5 24 7 20 18 13 14 17 12
Of the numbers from 1 to 24, the same ones are red and black as in regular Roulette, since as one ends the layout early at that point, the number of red and black numbers remains equal. (As should not be surprising, the wheel follows the European convention of having the tops of the numbers facing outwards, and so the numbers are read clockwise.)
As the wheel has 25 spaces and one zero, the house percentage is 4%, higher than that of European roulette, but lower than that of American roulette.
The game of Boule has an even higher percentage.
The wheel has 18 compartments, with the numbers from 1 to 9 in order twice. (Tops outward, clockwise.)
The layout looks like this:
------------------- | LOW 1234 | |-------------------| | | 1 | ODD | 2 | | |B|---| 1379 |---| | |L| 3 |-------| 4 |R| |A|---| 5 |---|E| |C| 6 |-------| 7 |D| |K|---| EVEN |---| | | | 8 | 2468 | 9 | | |-------------------| | HIGH 6789 | -------------------
As 5 is counted as neither high nor low, neither red nor black, and neither even nor odd, it plays the role of the zero, so the house advantage is 1/9th or 11.1111...%.
The red numbers are the ones in the column on the right, 2, 4, 7 and 9; the black numbers are the ones in the column on the left, 1, 3, 6 and 8.
Another gambling game resembling Roulette seen in France appears to have had an even higher percentage. It appeared in several forms, under several different names, one of which was Rodet; it involved a wheel with 24 compartments, twenty of which contained the numbers from 1 to 20, the other four having various kinds of zero; in one example, 0 simply occurred four times; in another, the four playing card suits appeared, and in another there was 0, 00, and a star, and presumably a fourth symbol which I have not seen.
Little is known about the origins of Roulette. An old game, played with a wheel similar to the Roulette wheel, is E. O., where the wheel has 40 compartments; players bet on "E" or "O", standing for even or odd, and the wheel is marked with the letters E and O alternating, but with one E and one O marked as barred, thus only returning the player's stake if they win. Thus, the wheel's house advantage is as if one out of 40 spaces was a zero, or 2.5%. But it is not clear if E. O. is older than Roulette or not.
The game of Biribi had a layout with numbers in order on which bets were placed, some Biribi layouts had extra spaces for certain groups of numbers similar to what a Roulette layout has. In Biribi, there was no wheel, the numbers were on slips of paper drawn from a bag. Usually, the layout was larger than that for Roulette. One layout used the numbers from 1 to 70, with the numbers from 33 to 38 treated as zeroes, somewhat reminiscent of the layout for Boule. There were also layouts for Biribi that used only 64 numbers, and only 36 numbers.
It is possible that one layout for Biribi looked something like this:
The house percentage would have been quite high.
Wagering on red or black, or on high or low, since there were 70 numbers of which 6 were zeroes, would have involved a house percentage of just over 8.57%.
At the top of the layout were the digits 1 to 9 and 0. For those bets, in order that each one would involve an equal number of possibilities, the numbers from 33 to 38 would not have been treated as zeroes or as in any way special; instead, the bets there would simply be paid at odds of 8 to 1, for a house advantage of 10%.
The yellow circles would allow one to bet on a column of the layout. The one in the center, for the column of "zeroes", presumably would be paid at 11 to 1, while the other ones would be paid at 7 to 1, and in each case the house advantage would be 8.57% also.
As for bets on individual numbers, I had suspected that instead of a house percentage of 8.57%, these bets at higher odds would also face a higher percentage; for example, perhaps a bet on a single number would be paid at 59 to 1, one on two numbers at 29 to 1, and one on four numbers at 14 to 1; making the house percentage on these bets equal to just under 14.29%, one part in seven. However, I have found at least one contemporary source for the game of Biribi that indicates that this was not the case, instead, such bets were indeed paid at 63 to 1, 31 to 1, and 15 to 1, for the usual percentage of 8.57%.
While there is no confusion on the layout about the fact that the six green numbers in the middle are neither red nor black, and it's also clear that they aren't on the high side (39 to 70) or the low side (1 to 32), they're still odd and even. So instead of having a space for bets on odd and even on this layout, there are spaces, each paying at 3 to 1 odds, and each with a house percentage of 8.57%, for the four combinations of red and black with odd and even. Thus providing another choice of odds, and making things simple to avoid any arguments.
In the 19th century, a game something like Roulette, but using playing cards, with a relatively high house percentage, was sold under the name of Diana.

Two decks of cards were shuffled and placed in a shoe. The first two cards were drawn face down, and the third card was the one that decided the bets.
There were four even-money bets: red and black, and high and low. Low would be Ace to Six; High would be 7, 8, 9, 10, Q and K. Red and Black also lost if any Jack turned up.
The even money bets, and bets on a suit at 3 to 1 (but note that the odds are printed 3 for 1 for bets on the suits! That would be a 25% house advantage if the Jacks were allowed to win; if not, that would be 30.77%, which, sadly, is not impossible) would have a high house percentage of 7.69%, or one part out of thirteen.
Betting on the jacks, like betting on any other rank, paid 8 for 1, or 7 to 1, and betting on an individual card paid 32 for 1, or 31 to 1. So these bets had an even higher house percentage of 38.46%, or five parts out of thirteen.
However, I have seen a photograph of an actual Diana layout, offered for sale at auction, which had somewhat better odds. The odds for a suit were printed on it as being 3 to 1, so the percentage would be 7.69%, and the odds for a rank were 8 to 1, so the percentage would now be 30.77%, "only" four parts out of thirteen. I don't know if the payout for individual cards was also correspondingly increased to 35 to 1.
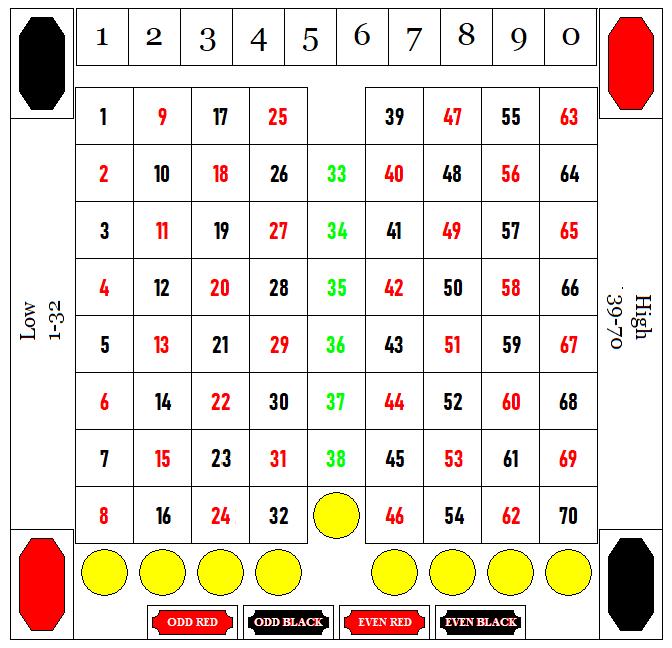
Also, there are new modern variations. At least one modern version of Roulette with 60 numbers and two zeroes is played with a physical wheel somewhere, under the name of Super 62 Roulette; Roulette with 100 numbers and five zeroes is offered for online gaming.
I have managed to find more information about Super 62 Roulette. It turns out that this game is proprietary, having been invented by Nicholas Sorge for Empire Global Gaming.
The arrangement of numbers on the reel (counter-clockwise, with the tops facing the center and the bottoms facing outwards) is:
0 5 36 57 18 39 60 1 22 43 4 25 56 17 38 39 20 21 42 3 24 45 16 37 58 19 40 41 2 23 44 00 10 31 52 13 34 55 6 27 48 9 30 51 12 33 54 15 26 47 8 29 50 11 32 53 14 35 46 7 28 49
The numbers on the layout are arranged in five columns, with the black numbers shown here as underlined:
1 2 3 4 5 -- -- 6 7 8 9 10 -- -- 11 12 13 14 15 -- -- -- 16 17 18 19 20 -- -- -- 21 22 23 24 25 -- -- 26 27 28 29 30 -- -- 31 32 33 34 35 -- -- -- 36 37 38 39 40 -- -- -- 41 42 43 44 45 -- -- 46 47 48 49 50 -- -- 51 52 53 54 55 -- -- -- 56 57 58 59 60 -- -- --
Thus, on the wheel, 49 is black and 5 is red, 44 is black and 10 is red, so both zeroes are preceded by a black number and followed by a red number.
There is only one photograph that I could find on the Web of a roulette wheel made in this fashion, on which four numbers were not visible, but the whole pattern of numbers on the wheel could be seen in U.S. patent 7,637,503 B2; the game itself was the subject of patent application 11/725,073 but that, apparently, did not lead to the grant of a patent.
This version, with two zeroes and 60 regular numbers, has an advantage substantially lower than that of American roulette, but still somewhat higher than that of European roulette.
Another version with more numbers, invented by Eric Joseph Kriznik in Slovenia, cuts the advantage of the house to half of the value found in European roulette, except perhaps for the even-money bets. At least one source says the percentage is the same on every bet, implying that there is no prison rule for Roulette 73.
A wheel for this game is pictured in the Cammegh catalogue, so apparently it is played somewhere.
The arrangement of numbers on the wheel is based on that of the European roulette wheel. Start with the numbers on the European wheel. Then, except for the zero, follow each number with a number of the same color, but from the second half of the layout.
The order of the numbers on the wheel is:
0 32 68 15 51 19 55 4 40 21 57 2 38 25 61 17 53 34 70
6 42 27 63 13 49 36 72 11 47 30 66 8 44 23 59 10 46
5 41 24 60 16 52 33 69 1 37 20 56 14 50 31 67 9 45
22 58 18 54 29 65 7 43 28 64 12 48 35 71 3 39 26 62
so the number following each of the numbers from the original European roulette wheel is the number 36 greater than it; in this way, the wheel takes full advantage of the properties of the European roulette wheel, and does not try to develop a novel random-seeming order of the numbers that players would need to come to trust.
This version of Roulette is called Roulette 73. The layout simply shows the numbers in six columns, and so red and black numbers on the layout do not have a simple and obvious pattern any more.
Also of some interest are two variant forms of Roulette devised by IGT which currently only exist for electronic on-line play, Double Bonus Spin Roulette and Triple Bonus Spin Roulette.
The first is claimed to return 98.06% of wagers to the player, the second, 98.11%, so both have a house advantage slightly less than that of European Roulette.
The arrangement of numbers on the wheel is, in both cases, based on that of the European roulette wheel.
For Double Bonus Spin Roulette, 0 is between 26 and 32, as usual; 00 is between 1 and 20, and B, on a yellow space, is between 27 and 13. Going clockwise, there are 13 numbers between 00 and 0, 11 numbers between 0 and B, and 12 numbers between B and 00.
For Triple Bonus Spin Roulette, again 0 is between 26 and 32, 00 is between 20 and 14, B, again on a yellow space, is between 10 and 5, and 000 is between 13 and 36. So, going clockwise, there are 12 numbers between 00 and 0, 12 numbers between 0 and 000, 6 numbers between 000 and B, and 6 numbers between B and 00.
To understand the principle behind these games, imagine that all one had was a double-zero American roulette wheel, but one wanted to offer people the lower percentage of European roulette. One way to do that would be to simply ignore the result, and spin again, whenever a 00 came up.
One could do something similar to reduce even more zeroes to a single zero. If one has a triple zero wheel, one way to make its percentage equivalent to a single-zero wheel would be to treat both 0 and 00 as zeroes, but if 000 comes up, instead of taking bets on other numbers away, spin again with a special bonus spin that pays double - once to eliminate 000, and once to eliminate 00.
And with four zeroes, one could have the fourth zero give triple pay to leave only one zero of house advantage.
Instead of one spin that pays double or triple, the bonuses in Double Bonus Spin Roulette and Triple Bonus Spin Roulette give two or three extra spins respectively - and this is done by means of an animation; in Double Bonus Spin Roulette, instead of a ball, two lights are shown as appearing in random pockets of the wheel; in Triple Bonus Spin Roulette, the roulette wheel is replaced by one with three rotating bands of numbers but still one ball.
To further improve the situation for the player, the bonus space in Double Bonus Spin Roulette is made 1.5 times as wide - and thus 1.5 times as likely to come up - than the other spaces on the wheel. The one for Triple Bonus Spin Roulette is also expanded, but not by quite as much - to 1 1/3 the width (the first source I saw said 1.3 times, but 1 1/3 is confirmed by the calculation of the house percentage below) of the other spaces on the wheel.
One can bet on the Bonus space on the wheel; that is done at reduced odds, because the bet is also eligible for special large prizes during the bonus spin.
In Double Bonus Spin roulette, a bet on B pays 11 to 1, a bet on B and one zero pays 5 to 1, and a bet on B and all two zeroes pays 3 to 1. If a B comes up in one of the bonus spins, one wins 120 times one's bet, and if it comes up in both bonus spins, one wins 1,200 times one's bet.
In Triple Bonus Spin roulette, a bet on B pays 11 to 1, a bet on B and one zero pays 5 to 1, a bet on B and two zeroes pays 3 to 1, and a bet on B and all three zeroes pays 2 to 1. All those bets make one eligible to win 1,200 times one's bet if two of the three bonus spins come up B, and 12,000 times one's bet if all three of the bonus spins come up B.
Usually, a game offering special features for more excitement will also have a higher house percentage. Why is this game so generously offering a lower percentage than European roulette?
For one thing, an online casino has much less overhead than a real one that has to pay a salary to a human croupier. For another thing, while the house percentage influences how much money a casino makes, because players will usually take their winnings and bet them again, the proportion of the money that players bring with them to play that the casino retains is usually several times the percentage. So a slightly lower percentage in exchange for keeping players more interested is not a problem.
Let us attempt to calculate the house percentage for the regular Roulette bets in Triple Bonus Spin Roulette.
Let us assume the Bonus space is indeed 1 1/3 times as likely as a normal space to come up.
Of 40 1/3 chips wagered by the player, then, 36 are returned in the normal manner by winning numbers coming up directly on the spin.
There will also be 1 1/3 triple bonus spins (on average). Here, the bonus space counts as just another zero; each bonus spin again returns 36 parts out of 40 1/3 parts of what is wagered.
So the player pays 40 1/3 chips, and recieves 36 chips plus 4/3 * 9 * 36/121 chips, which comes out to 39.57... chips out of 40 1/3, or 98.1080527286385754...% of what is wagered.
Of course, the percentage on the bets on the bonus, with large payoffs, will be higher.
The number 36 is equal to 4 times 9. On the other hand, the number 24 is equal to 3 times 8, and so it offers what is perhaps a more attractive selection of odds for different bets. But the number 30 would be even better, being 2 times 3 times 5.
But if one chooses to play on a wheel with 24 numbers and one zero, or even 30 numbers and one zero, one faces a higher percentage than on a wheel with 36 numbers and one zero, although a lower one than on a wheel with 36 numbers and two zeroes.
If only one could play whatever kind of roulette one liked, with 24 numbers, with 30 numbers, or with 36 numbers, without the percentage changing, with the same low house percentage for all three games!
One way would be to have no zeroes, and a percentage fee for all bets, but that is too complicated.
24, 30, and 36 are all multiples of six. So one could have a wheel with 24 numbers and four zeroes, a wheel with 30 numbers and five zeroes, and a wheel with 36 numbers and six zeroes... and they would all have the same house advantage, one part in seven!
That solves half the problem, the percentages are all the same now, but they are terribly high, not low at all!
But wait... if single-zero Roulette cuts the percentage in half on the even-money bets with the prison rule, perhaps something similar could be done to adjust the percentage of this game to what is wanted?
And so here is my idea.
Have the wheel marked with four, five, or six seroes to accompany 24, 30, or 36 numbers respectively.
When a zero comes up, no bets are either paid or removed from the layout.
When the wheel is spun again, if a number other than zero comes up, all bets are either paid in full or taken, normally, as if the zero had not come up on the previous spin.
If zero comes up a second time, however, all bets are lost - except for bets on zero (or perhaps on 00, to indicate obviously what the rule is doing), which are paid at 47 to 1.
In this way, no matter which wheel one plays on, the house advantage is low, as if one is playing on a wheel with 48 numbers and one zero.
Thus, the house advantage is lower than on the European roulette wheel with 36 numbers and one zero, except for the even-money bets. This can be fixed, of course, by also having the conventional prison rule for those bets: when they are lost due to zero coming up twice, then they are put in prison, and the next spin determines if they are truly lost, or simply returned as barred. It is simplest and most consistent for two more zeroes, rather than just one to be a loss on the next spin for that purpose.
You have heard the phrase "Less is More"; here, more zeroes is less of a house advantage! But is one zero with 48 numbers too low a house percentage to be practical?