The ancient Romans, in addition to using normal six-sided cubical dice, also sometimes played games with dice having fourteen sides, in the shape of a cuboctahedron. Such dice have six large square faces, and eight small triangular faces.
Given that the square faces are more likely to come up than the triangular ones, but by a proportion it is not really possible to determine, are such dice useful for playing games?
It does not seem that a real problem would be caused if one were to use one die of that type for playing a game of Snakes and Ladders. But other types of games seem to require an exact calculation of odds. What if one were to try to adapt the rules of, say, Bank Craps to such dice?
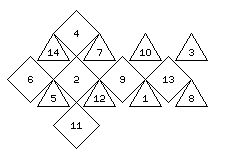
Let us assume the faces of the die are numbered in a symmetrical fashion, taking into account the distinction between square and triangular faces:
Triangular: 1 3 5 7 8 10 12 14 Square: 2 4 6 9 11 13
The faces might have the arrangement illustrated below:

Throwing two dice produces a total from 2 to 28, and 15 would presumably be the most likely total. If the chance of a triangular face coming up is p, and the chance of a square face coming up is q, then we believe that p is less than q, and we know that 8p + 6q equals 1. The chances of the different totals are:
p*p p*q q*q
2 28 1
3 27 2
4 26 2 1
5 25 4
6 24 3 2
7 23 6
8 22 4 3
9 21 2 6
10 20 3 4 2
11 19 4 4 2
12 18 2 8 1
13 17 6 2 4
14 16 1 12
15 8 6
If two players each roll the dice, and the one with the highest total wins, the odds would, of course, be fair regardless of the type of the dice used.
A game with specific odds quoted for specific rolls of the dice is also possible, if the layout were divided into three independent sections, one for rolls of two square faces, one for rolls of two triangular faces, and one for rolls of one square face and one triangular face, and in each case, rolls not applicable to a section were simply ignored for wagers there.
If the square faces were numbered from 1 through 6, and the triangular faces from 0 to 7, many games played with ordinary dice might be able to be played with only a very slight adaptation. Even without taking such a step, it should be able to achieve something.
If one were to start a series of rolls of the dice described above with the totals of 14, 15, and 16 winning immediately, these add to 10, 24, and 6 combinations in the three columns respectively.
If, on the other hand, totals from 3 through 7 and 23 through 27 lost immediately, these combinations also add to 10, 24, and 6 combinations in the three columns. So, if a total of 2 lost, and a total of 28 won, the chances of winning or losing on the first throw would be even.
If one throws another low number, from 7 through 13, then one might win if one throws a number from 2 through 14, lose on a number from 16 through 28, and roll again on 15; if one throws another high number, from 17 through 22, one might win if one throws a number from 16 through 28, lose on a number from 2 through 14, and roll again on 15. This would be similar to Craps, but quicker, and with dead-even odds, despite the fact that the shape of the dice makes the exact odds of the combinations unknown.
The analogous game with conventional dice would be to win immediately if one throws a 7 on the first throw, to lose immediately with 2, 3, 11, or 12, and if one throws a number from 4 to 6, one's point is "low", and one wins if one throws a number from 2 through 6 before a number from 8 through 12; if one throws a number from 8 through 10, one's point is "high".
One could also consider 26-sided dice, which have eight triangular faces, and a group of six square faces surrounded by square faces, and twelve square faces bordered by two square faces from the other group, and two triangular faces.
These could be numbered like this:
Triangular: 2 5 9 12 15 18 22 25 12-Square: 1 4 6 8 10 13 14 17 19 21 23 26 6-Square: 3 7 11 16 20 24
so as to make the numbering on each kind of face spaced as evenly as possible.
While it may again be quite rare for the triangular faces to come up, both kinds of square faces would normally come up in practice, even if the 6-square faces would be individually about twice as likely.
You may wish to go to a related page, where I discuss ancient Greek and Egyptian dice, such as the green glass one which made the headlines when it was sold at auction for about $20,000.