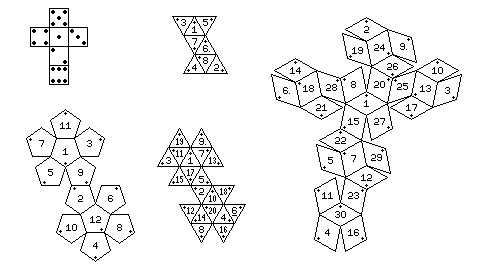
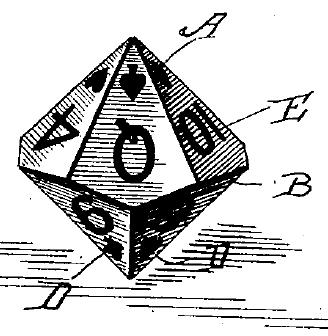
On a related topic, given how the numbers are arranged on ordinary dice, and to alternate high and low numbers, the arragements of numbers shown here seem to me to be appropriate ones for polyhedral dice; and the existence of an arrangement not devised by a manufacturer seeking to keep its competitors from copying its own arrangement might even lead to all polyhedral dice being made the same way, the way cubical dice are (although it could well be, particularly for the d8 and d12, that the arrangements shown here are already taken):
Of course, the question of why one wouldn't want to get the attractive special polyhedral dice, now that they are inexpensive and easily available, comes up too, but to have a way one could manage in a pinch is always useful.
The numbers are all shown upright, for ease of drawing, so the dots in the triangles, pentagons, or rhombi are present to show how the numbers might actually be oriented, indicating the corner towards which the top of the number would be directed.
It wasn't that long ago that dice were six-sided cubes, and that was that.
Even the arrangement of spots on a die is uniform around the world, as shown in the top half of this diagram:
In the middle, however, is shown another arrangement of spots on dice sometimes encountered in ancient times, where instead of opposite sides of a die containing numbers of spots that add to 7, the opposing pairs are adjacent numbers; 1 and 2 are opposite, 3 and 4 are opposite, and 5 and 6 are opposite.
Dice from Harappa that are thousands of years old followed this arrangement, and Etruscan dice from before 500 BC were also arranged this way, while those from after 350 BC were arranged in the current fashion, which came to us from them through ancient Rome.
Finally, on the bottom, is shown a still more rare arrangement of numbers, where the 5 is opposite the 4, and the 6 is opposite the 3, as these numbers add to nine, found on dice used for divination from Tibet to Mongolia. However, this arrangement has many variations; sometimes while 5 is placed opposite 4, the opposition of numbers that total to nine is not taken further.
Dice with spots are used in one form of Tibetan divination which uses three dice, known as Palden Lhamo divination; the better-known system of Tibetan divination with dice, however, uses dice with letters or syllables from the Tibetan abugida, and is known as Mo. Images of dice for this on the Internet show many different arrangements, and so the arrangement in the diagram below is not to be taken as a recommendation:
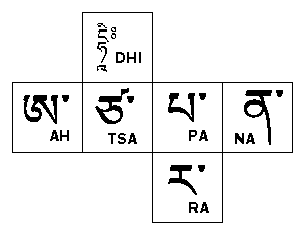
Although I tried, by using the correspondence given between these symbols and spots, if ordinary dice are used, from one source, and the arrangement of spots on traditional Tibetan dice shown in the diagram above. It could have been, though, that the correspondence was given to put the symbols in their proper locations on a die if common Western dice were used, rather than that being intended as an inherent numerical correspondence of the symbols, in which case I would have it wrong.
In ancient Rome, fourteen-sided dice in the shape of a cuboctahedron were sometimes used. Well, at least they have one of them in the British Museum, and it appears that the numbers on it were arranged so that the numbers from 1 through 6 were on the large square faces, and the numbers from 7 through 14 were on the small triangular faces. The assignment of numbers to the faces appears to be as shown in the diagram below:
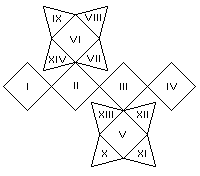
From this, I conclude it was likely to have been used for some game where two, or possibly more, players took turns throwing the same dice, and competed to reach the highest total; for such a game, the fact that large numbers were harder to attain would not be an issue, it might even have seemed natural.
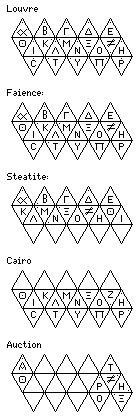
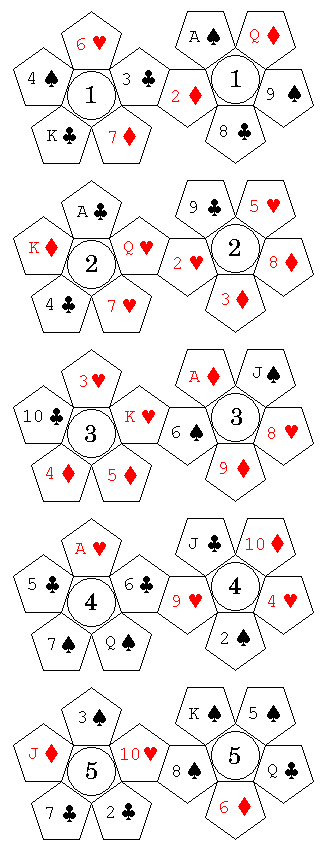
The New York Metropolitan Museum of Art once exhibited two ancient Greek icosahedral dice, one in faience and one in steatite engraved with the letters of the Greek alphabet. They have graciously made one image of the one in steatite available in the public domain, as I learned through the collection of images at Wikipedia, and thus I have included this image on the left. Recently, a glass blue-green icosahedral die made the news when sold at auction. It had appeared to me that this die was engraved with unusual symbols, perhaps astrological in origin. However, the Louvre museum also has an icosahedral die with similar symbols on its faces. from Egypt during the Ptolemaic period, and images of a reproduction of that die are on the Dice Collector web page: this die clearly has Greek letters on its faces, implying that what seemed to be astrological symbols were stylized or script forms of Greek letters. A rhombic dodecahedron with letters on its faces is also in the Louvre.
The arrangement of letters on the one in the Louvre in particular, and on these dice in general (sometimes with rotations of the three segments relative to each other) is shown in the top diagram in the image at the right.
The Greek letters from alpha to upsilon are present on these dice.
The top cap of five triangles shows the letters alpha, beta, gamma, delta, and epsilon; the one unusual thing is that alpha is written in a squared form, reminiscent of runes, and in the script or lower-case form, whereas the others are in the form we are used to for Greek capital letters.
The middle band shows the letters from zeta to omicron. They are shown starting with theta, and wrapping around, so the order is theta, iota, kappa, lambda, mu, nu, xi, omicron, zeta, and eta. Two letters are in an unexpected form. Theta is written as a circle with a dot in the middle, like the astrological symbol for the Sun, rather than with a line across the middle. The letter zeta is written in a script or cursive style, with loops at the two corners in the letter, so that it cannot be confused with nu.
The bottom cap of five triangles shows the letters from pi to upsilon. They are shown starting with sigma, so the order is sigma, tau, upsilon, pi, and rho. Sigma is written like the Roman capital letter C, which avoids confusion with mu; Upsilon is written like a capital Y, which is common even in present-day Greek-language typestyles.
If one assumes that the same pattern is employed in some of the other dice of this type I have seen pictured on the Web, some parts of their arrangements can be inferred beyond the portions actually visible. Thus, the one in faince seems to have the same arrangement of letters as on the one in the Louvre, but, at least on the visible faces, seems to have the orientations of the letters arranged more systematically. This was an image I saw on Flickr; the text seemed to imply that the image was of an item on temporary loan, and another search result indicated that a faience die of this type belongs to the British Museum. Of course, more than one may have survived, so I can't infer with certainty that this was their specimen on loan.
The one in steatite at the same exhibition seems to have had the letters in a slightly different position, with the central band rotated relative to the cap with the letters from alpha to epsilon. None of the letters in stylized form were visible in the photograph, so I can't be sure what forms were used for them on this specimen.
Someone else placed a photograph on Flickr of a display case containing several icosahedral dice in a museum in Cairo that he had seen. He had done so for a particularly poignant reason, having seen these ancient d20-like dice on the same day that E. Gary Gygax passed away. One die was clearly enough visible in the photograph so that several of its letters could be made out; it, too, could follow the same pattern as the others, if one assumes that one of the letters is a zeta not drawn in a stylized script form rather than an eta.
The glass one sold at auction by Christies recently for over $17,000 uses the same stylized forms as the one in the Louvre for zeta and theta, but a different form for alpha, but the letters must follow a different order; this isn't actually particularly surprising.
I suspect these dice were used for divination rather than for a game; at this site is an ancient Greek set of divinatory meanings for the 24 letters of their alphabet.
Once, I encountered a 26-sided die in the shape of a small rhombicuboctahedron for playing a baseball game on a board in a thrift shop, but failed to snap it up, and I did have a set of octahedral poker dice, so there may well have been occasional exceptions during the 1960s and before; in the 1930s and perhaps even in the 19th Century.
When cubical dice were first used in ancient times, they were usually made from bone, but sometimes they were made from ivory, wood, metal, or polished stone.
In the earlier part of the 20th century, dice were usually made from plastic, but occasionally inexpensive wooden dice would be packaged instead with some children's games.
But dice can still be made from materials other than plastic; thus, some high-quality dice made from wood are pictured below, along with dice made from polished stone:
Casino dice had sharp edges, while some Chinese-made dice would have corners so rounded as to be spheres with six shallow domes removed to leave six flat circular faces. Not all Chinese dice are that rounded, but a pronounced rounding of the corners is characteristic of dice made according to that pattern.
Here is an image of three dice in the Chinese style. In addition to having rounded corners, note that the two rows of dots on the six are closer together, and the two dots on the two are in an orthogonal line instead of a diagonal line like the dots on the three. As well, the dot for the one is enlarged, and the dots for the one and the four are red.
This last characteristic was introduced into the photo above by retouching it in a paint program; while at one time, dice in the Chinese style were very common accompanying inexpensive board games, these days manufacturers in China have become more sophisticated about the demands of Western markets - even the manufacturers of these dice, which I picked up in a dollar store, which were made from molds designed for dice of the Chinese pattern, but which had all the spots painted black as these were destined for a Western market.
The story I had always believed about why those dots were red on Chinese dice was because red is considered an auspicious color among the Chinese, and, at least in Cantonese, the word for the number four sounds like the word for death; the word for one sounds like the word for "certain", thus also making it a participant in the problem.
However, in searching for more information, I have found that there is another story current: a Chinese Emperor was playing a dice game with one of his wives or concubines, and he was on the point of losing; the only roll that would allow him to win was a four - and so he asked for a four out loud, and a four came up.
In honor of that event, he decreed how dice were to be colored henceforth.
Many versions of that story also name the game - calling it sugoroku.
I have my doubts about that. Sugoroku is, of course, a Japanese word. Of course, the Chinese do play wei ch'i (or, as they would transliterate it today, weiqi) even if the English-speaking world knows it by its Japanese name, Go.
The English-speaking world also knows sugoroku by another name... backgammon. The Japanese learned the game from Western sailors, and it became such a craze in Japan that the Emperor banned it. With the exception that the sisters at one particular Buddhist convent in Japan could continue to enjoy that game as recreation.
I had been quite doubtful of this story, but after a web search, I found that backgammon was known as Shan-Liu in China, and was quite popular there around 700 AD, and remained popular with the elite after it faded from more general popularity. As well, there was a Chinese game of the same general type known as Coan Ki, and so either game could have formed the basis of the legend.
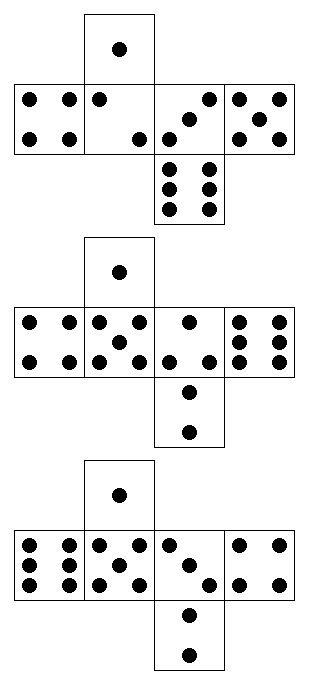
Sometimes, dice used for various types of game, although still having the standard six sides, would have other markings on them than the usual sequence of from one to six spots. There were poker dice, with card symbols on them, both in sets of five identical dice, and in sets where two of the five dice had one space showing a Joker, and the other 28 available faces showed the 8, 9, 10, Jack, Queen, King, and Ace of each of the four suits, so as to allow the same hands, including flushes, to be made as in Poker played with playing cards, instead of being equivalent to playing poker dice with five ordinary dice. There were dice for Crown and Anchor, and even dice for Hoo Hey How with pictures of a fish, a prawn, a crab, a rooster, a gourd, and a coin for a similar game. (The Vietnamese version, Bau Cua Ca Cop, replaces the coin with a stag, and there are a number of other variations.) There were dice with letters on them for word games.
For now, I will just illustrate this with an image of the most common type of poker dice, where all six dice are identical:
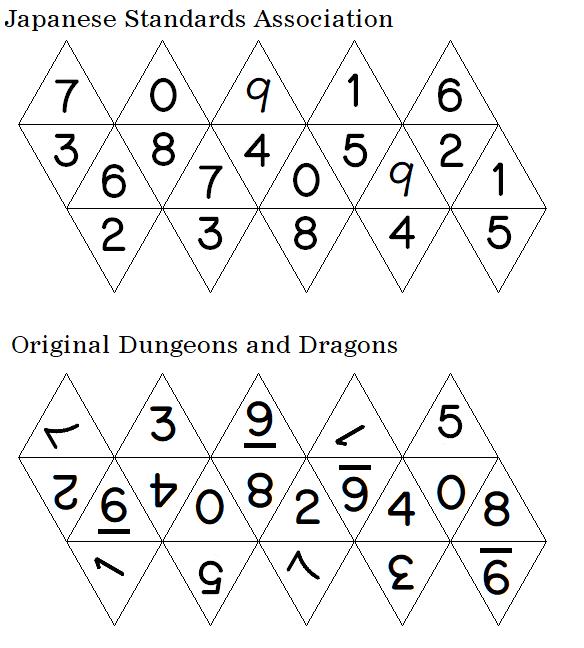
In 1966, the book Random Number Generators by Birger Jansson was published. This book was chiefly concerned with algorithms for generating pseudo-random numbers deterministically on computers for simulation purposes. The cover showed a set of three icosahedral dice of different colors, each one with the digits from 0 through 9 on them, repeated twice. These dice were distributed by the Japanese Standards Associatiion to facilitate random sampling, and were expensive due to the limited production.
The Dice Collector web site features a set here, and I was able to learn more information about them there.
Instead of distinguishing the 6 from the 9 with an underscore or a dot, or simply by placing each digit in the same orientation with respect to the triangular faces of the die, the 9 was distinguished by being in a script form, unlike the other digits.
When I came across this book in the early 1970s, I felt the hope that such dice would someday become conveniently available.
Of course, this did happen. But it did not happen in isolation, because some educational toy company decided to make a probability kit available. No, it happened as an incidental result of an Earth-shaking social change in how people amused themselves in their spare time!
It is, of course, to the game Dungeons and Dragons that I refer, which first appeared in 1974.
Because of limited demand and limited capital to set up production facilities, at first the available polyhedral dice were less fancy than those sold at present; purchasers would have to paint the numbers molded into the dice themselves to make them easy to see, and the type of plastic used was less expensive than what is most common at present. A set of dice would consist of one each of the five Platonic solids,
Here is an image showing the layout of numbers on these two historic icosahedral dice:
I have recently learned, from two web sites, a bit more about the history of the polyhedral dice used with Dungeons and Dragons. From the site of Playing at the World, the page on How Gaming Got Its Dice, and from Bombard Games, The History of Polyhedral Dice in Board Games.
U. S. Patent 3,208,754 was issued on February 20, 1963 to Fredda Sydney Sieve for a "Dice Game with a Tetrahedron Die". The tetrahedron die was shown with only one number on each face, and so it was read by taking the number that was missing, from the numbers from 1 through 4, from the ones that were visible. But the set of dice for the game included all the Platonic solids, and the icosahedron bore the numbers from 1 to 20.
The game was called Zazz, sold through Advertising Attractions Incorporated of New York, and it was available at least until 1965.
The story of that game is on this page, also from Playing at the World.
One set I've seen pictured had a purple d4, a blue d6, a green d8, a white d12, and a red d20. A news clipping about Fredda Sieve notes that she was the widow of a scientist named Benjamin Sieve. I don't know if he was Benjamin F. Sieve, who is noted as the discoverer of the birth control pill, and who died by suicide.
Interestingly enough, the dodecahedral paperweights bearing on their faces calendar pages for the months of the year which were once seen in many doctors' offices were also an earlier Fredda Sieve patent, from 1956!
Also predating Dungeons and Dragons were a set of two icosahedral dice, intended for use as percentile dice, available from the Bristol Wargaming Society some time around 1970.
A video on YouTube from Ben Johnson, titled "Polyhedral Dice, Why Are They", tells the story of how polyhedral dice got into Dungeons and Dragons in detail, and there is even more detail in this Wikipedia article. A group of friends who played wargames, under the name of the Midwest Military Simulation Association, had one David Wesely as a member; he was researching old wargames, and found a reference to a teetotum with the numbers 1 through 12 on it. He considered a dodecahedron as an alternative, and found models of the Platonic solids in what accounts typically refer to as a school supply catalog. The game the group invented in which they were used was called "Braunstein".
In the video, however, the illustration of the catalog from which the shapes was ordered shows a page from a catalog not specifically aimed at teachers and schools, but aimed at all people in the general public interested in science: the famous Edmund Scientific catalog. Here is the entry for that set from page 40 of Edmund Scientific Catalog 671, for 1967:
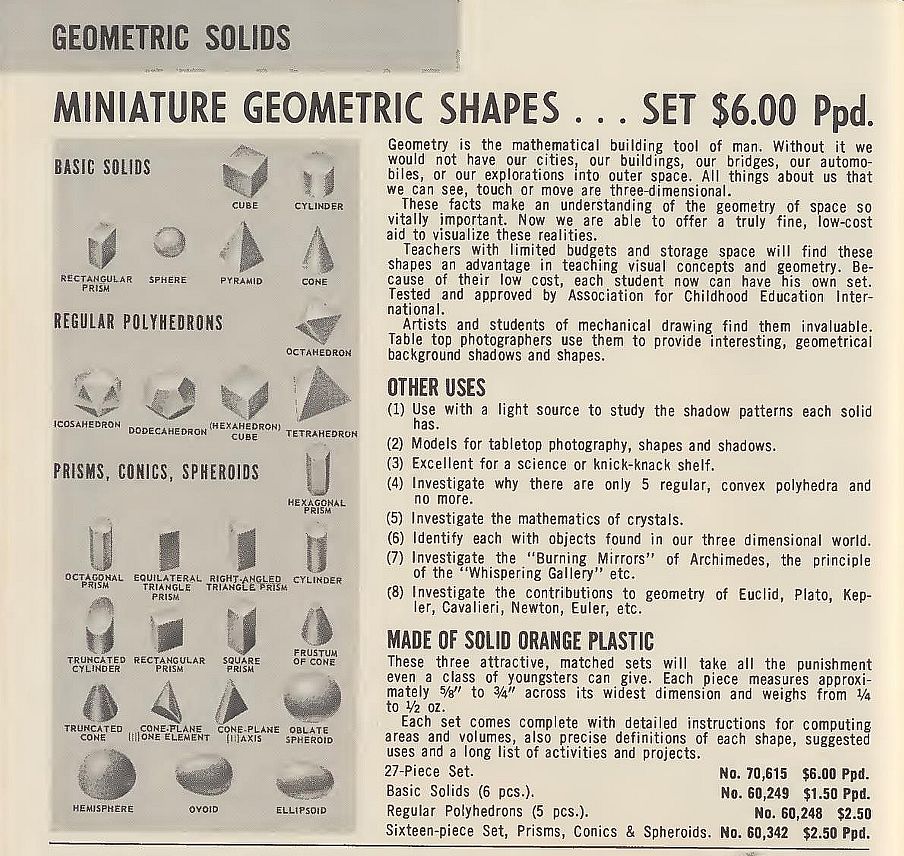
However, it is possible that this one simply appeared to illustrate the set because this catalog is more easily available than the school supply catalog he actually ordered from; I am not yet completely sure of this.
Another member of that group was Dave Arneson, who co-created Dungeons and Dragons with Gary Gygax, and this is how the idea of using polyhedral dice got included in the game.
Although Braunstein was inspired by Diplomacy, even in that game, the players had roles they were playing. Dave Arneson later developed the game to a version called "Barony of Blackmoor", in a fantasy setting, which appears to have included more elements of Dungeons and Dragons.
However, Dungeons and Dragons is largely based on Chainmail, which was developed by Gary Gygax before he joined forces with Dave Arneson; and then Dave Arneson made use of the Chainmail rules when developing Barony of Blackmoor, and so it isn't a mistake to view him, and not Dave Arneson, as the primary inventor of D&D, despite how the story of polyhedral dice as I learned it and recounted it above made it seem for a moment.
Like Barony of Blackmoor, which had David Wesely's Braunstein as an antecedent, Chainmail also was preceded by Henry Bodenstedt's Siege of Bodenburg, though, it should be noted.
The dice first included with a Dungeons and Dragons product, those included with the Dungeons and Dragons Basic Set in 1977, were known as the Holmes dice, because J. Eric Holmes wrote the books included with that set.
These dice were very similar to an earlier set of dice made available by Creative Publications in 1972. The d4 was yellow, the d8 was green, the d12 was blue, the icosahedral d10 was white. In the Creative Publications set, the d6 was pink, while in the Holmes set, the d6 was red. Creative Publications was originally a supplier of polyhedral dice to TSR, which also sold such dice separately.
As sold directly from Creative Publications, the dice set included an instruction sheet which suggests it was sold for use in mathematical education. One suggested educational activity was working out why the shapes of those dice, the Platonic solids, were the only possible shapes for fair dice. Of course, as more people know nowadays, that isn't true, but even some mathematics professors had, before looking in to the matter, fallen victim to that misconception - as one has admitted on YouTube. (I will be listing the best-known classes of shapes for fair dice on this page below in a few paragraphs from here.)
Incidentally, this page is one page (there are several) that does a better job than my page here of discussing the possible shapes for dice, so you may wish to pay it a visit.
Later, the quality of reasonably inexpensive polyhedral dice would improve, but ones with pre-painted numerals would still be significantly more expensive. The dice would have sharp edges, and would be made from ordinary plastics, such as polystyrene. During this period, icosahedral dice with faces numbered from 1 through 20 became available. Non-icosahedral dice with only ten faces supplanted the earlier form of icosahedral dice, starting with the version of the Dungeons and Dragons Basic Set edited by Tom Moldvay published in 1981.
Just recently, I found out that dice of this shape were described in U. S. Patent 809,293 from January 9, 1906. These ten-sided dice had playing card symbols on them, however, not the digits from 0 to 9. One A. Friedenthal was the inventor.
Here is a diagram from that patent:
A closely related type of ten-sided die can be made from a dodecahedron, by placing domes on two opposing faces. This was used to make a set of Poker Dice which included all but two of the cards of the deck (as opposed to how a modern set would work, by omitting all the deuces and then adding in two Jokers) sold as Montana Dice. Mason & Co. sold them under that name, and H. C. Evans & Co. sold similar dice under the name California Dice. As well, dice of the same shape, but with the digits from 0 to 9 on them, called Bank Clearing or Stock Exchange Dice, and apparently intended to help people guess numbers to play when playing the "Numbers Game" were sold by the K. C. Card Co. as well.
Except for the tetrahedron, the Platonic solids, when situated with one face down on a surface would have another face at the top. Tetrahedral dice, therfore, had three numbers on each face, either to indicate which of the four corners was at the top, or which of the four faces was at the bottom. One of the ways to make a perfectly fair ten-sided die would be to have two five-sided pyramids abutting each other. When such a die was resting on one face, however, an edge would be at the top.
While this could be dealt with by splitting the numbers across the edges, as has been done for five of the seven faces of (not perfectly fair) seven-sided dice in the shape of pentagonal prisms, this was unnecessary in this case. Instead, one of the two pyramids could be rotated 36 degrees, and the faces suitably extended into kite-like shapes to join properly. This is the shape currently used for the d10, and a set of dice now normally contains one icosahedral d20, and two d10s of this shape, one of which has the faces numbered 00, 10, 20... 90, so that there is no ambiguity when rolling them. This shape is called a trapezohedron, the kite shapes being trapeziums.
This led to the typical complement of dice included in sets intended for playing role-playing games that are available today, as pictured below:
While I thought that a fancy clear set would make for a nicer illustration, now I see that it's a bit hard to see in the photo, so here is another image with the dice in the same layout, but with plain opaque dice:
I see, though, that the tetrahedral die in this illustration has one unusual characteristic: the active digit, of the three printed on each face, is close to the face that is on the bottom instead of the vertex that is at the top!
From left to right: a tetrahedral d4, a cubic d6, an octahedral d8, a twisted bipyramidal trapezohedral tens die for use in a set of percentile dice, the twisted bipyramidal trapezohedral d10 which also completes the set of percentile dice, a dodecahedral d12, and an icosahedral d20.
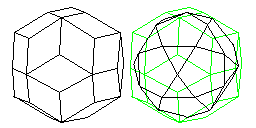
Another innovation from that period was the d30, based on the rhombic triacontahedron. These dice were introduced in 1982 by The Armory, and were initially available primarily by mail order.
Since 30 equals 2 times 3 times 5, and the number of faces on the five Platonic solids are 4 (2*2), 6 (2*3), 8 (2*2*2), 12 (2*2*3), and 20 (2*2*5), the roll of any of them could be replaced by from one to three rolls of a d30 (4: 2 rolls, 6: 1 roll, 8: 3 rolls, 12: 2 rolls, 20: 2 rolls), since 2, 3, and 5 are the only prime factors found in 4, 6, 8, 12, and 20.
The rhombic triacontahedron is the dual of the icosidodecahedron, as the diagram below illustrates:
The Armory did make available sets of tables for use with their d30, which included tables to allow it to be substituted for all the other dice in common use at the time.
However, it was instead the d24, in the form of the deltoidal icositetrahedron, which is the dual of the small rhombicuboctahedron, that was instead used as the basis for the D-Total, from Gamescience, the same company that gave us the Zocchihedron. It was first introduced in 2008.
Obviously, a 24-sided die can take the place of a d4, d6, d8, and d12 perfectly. But the legends printed on the faces of the D-Total are intended to allow it to also take the place of the d10 and d20, with the limitation that occasionally an invalid face will come up that requires the die to be rolled again.
The original D-Total was modified by printing some additional information on the faces of a newer version, to increase its versatility still further. The diagram below shows how to read the legends on the old and new forms of this die:
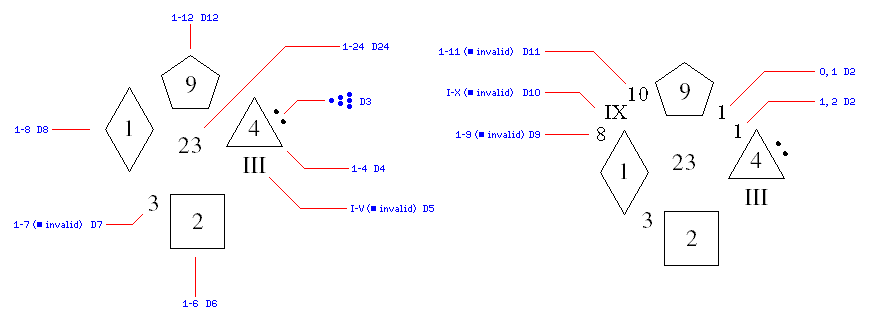
On the left is shown the original form of the D-Total. The legends printed on the die allowed it to directly function as a d3, d4, d5, d6, d7, d8, and d12 in addition to a d24. Of course, even without an explicit legend, it could be used as a d10 or d20 simply by rejecting rolls of 21, 22, 23, and 24 as invalid from the d24 number, and either using the other numbers directly for a d20, or their last digit for a d10.
On the right is shown the somewhat more complicated legend on the new, improved form of the D-Total. Here, it can also function directly as a d2 (instead of simply using, say, odd as 1 and even as 2), and, as well, explicit values are printed for use as a d9, d10, and d11.
Here is a photograph of one of the newer D-Total dice:
The duals of many of the other Archimedian solids are also suitable for making fair dice with other numbers of sides, such as 60 sides or 24 sides.
In some cases, though, the faces of an Archimedian dual (also known as a Catalan solid) instead of being absolutely identical, are identical except for parity reversal. A die made from such a solid could perhaps be rolled with a spin so as to favor half the faces over the other half. Thus, while a d60 and a d24 can be made without that problem, the closest one can approach to making a d120 and d48 with identical faces is to allow a parity reversal of half the faces.
As an icosidodecahedron is clearly more likely to land on its triangular faces than its pentagonal faces, and the truncated icosahedron is more likely to land on its hexagonal faces than its pentagonal faces, it seems reasonable to suppose that somewhere in between those two shapes, a fair die exists. But while a shape with hexagons with three sides made shorter so as to be equal in area to the pentagons might approach such a die, there is really no known mathematical way to determine exactly how a fair die of this type could be made.
The shapes that can be used to make fair dice that we can know to be fair are:
The first four of the five types of possible fair dice listed above belong to the class of shapes known as isohedra; all the faces are identical in shape, and identically situated with respect to the shape of the solid as a whole.
The number of possible fair dice isn't bounded; bipyramidal trapezohedrons for use as dice have been made with 34 and 50 sides. Of course, a very large number of sides will be impractical.
While a fair die with any number of faces is therefore possible, it is easier to make dice with some numbers of faces than others. Thus, one could make a bipyramidal die with 100 faces, but so far the only types of d100 made are based on shapes which aren't necessarily perfectly fair.
Of course, there is an oversimplification here.
Dice, like any other manufactured items, are made to certain tolerances with respect to their dimensions and the uniformity of their density. Plus, the pips on conventional dice, and the incised numerals on RPG dice, cause their shapes to depart from the geometrical ideal.
Thus, dice intended for use in casinos have sharp edges, because it's easier to see that the edges are sharp than that all the edges and all the corners are rounded by the same amount; they're made of a transparent material, so that weights can't be easily concealed inside of them; and the spots are filled in by opaque plastic having the same density as the transparent plastic of the die, so that they don't represent a deviation from the ideal cubical shape.
Here is a picture of a pair of dice of the kind used in casinos:
Weighted dice that look like casino dice have still been made despite these precautions: as the weights have to be concealed within the opaque plastic of the spots, this means expensive very heavy metals like tungsten or even platinum group metals tend to be used for this purpose. (Because of the toxicity of lead, tungsten has even been used to weight chess pieces, although usually iron is dense enough for that purpose.) So it just makes it harder to weight the dice, rather than impossible.
Why aren't all dice made this way? Apart from the extra expense involved in making casino dice because of their higher precision, the fact that their edges are not rounded means that they may not roll well; that is, they don't automatically tumble as much when rolled.
This problem is dealt with when playing craps in a casino by requiring that the dice be thrown so as to pass above a string, and hit the baseboard behind it, with a patterned surface; this ensures the dice are in a random orientation when they first hit the mat below, so that it does not matter if they only tumble a few times.
The dice used for RPG play are available with sharper edges as well as rounded edges, and with the greater number of faces on a d12 or d20, that presents no problem in how easily the dice tumble, and in transparent materials as well as opaque, but as far as I know, those characteristics haven't been combined with filling the numbers with plastic to have flush-numbered RPG dice similar to flush-spotted casino dice.
The most convenient numbers of faces are those available for the first two types of die listed above:
The Platonic solids, of course, have 4, 6, 8, 12, and 20 faces.
The Archimedian duals have:
Thus, the Archimedian duals make it very convenient to add dice with 24, 30, and 60 sides to the set of fair dice. The possibilities with 48 and 120 sides include faces which are mirror reflections of each other, which may be a departure from perfection, but dice of these shapes have also been made, although they are less common.
Although there is a dodecahedron with 12 sides among the Platonic solids, the rhombic dodecahedron has also been used to make a 12-sided die. The triakis tetrahedron, on the other hand, like the tetrahedron, doesn't have opposing faces, and so is less practical to use as a die.
Also, the list above is not exhaustive; for example, there are certain types of distortion that can be applied to at least some of the Platonic solids and some of the Archimedian duals which will still allow the distorted shapes to function as fair dice, because all the faces will be identical in shape, and identically situated in relation to the rest of the solid as a whole, and thus these shapes are additional types of isohedra.
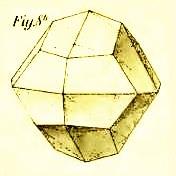
The above illustration shows one of the more nontrivial cases of this; but one can also take a Tetrakis Hexahedron, the common d24 shape with a pyramid on each face of a cube, and just make all the pyramids slightly taller or shorter, keeping all the same height, while the die remains convex, and have an isohedral fair die that is no longer the dual of the truncated octahedron, even though it still has the same general shape as it.
And, of course, dice with rounded corners can be fair, as long as the rounding is symmetrical. Here is a drawn illustration of a regular 6-sided die, which is in the shape of the intersection of a sphere with a cube having the same center, of such a size as to slice off enough of the sphere to give it six circular faces:
The first image should make it clear the sort of thing I speak of; at one time, inexpensive board games made in Hong Kong came with such dice, this being at one time the common style of dice in China; also, while the spots for other numbers were black, those for the numbers 1 and 4 were red; this is generally attributed to the fact that the words for the numbers 1 and 4, in Cantonese, had a similar sound to words with an unfortunate meaning. The second image is a photograph of a more conventional die with corners that, although less extremely rounded, are still significantly rounded.
Next, we will look at all the Archimedian duals, placed in order by the number of faces they have; this will make it easier to follow the subsequent discussion of the different types of dice made in those shapes.