As will be discussed in more detail later, an Archimedian solid with two different kinds of side can still be a fair die, if the two kinds of side are numbered repeatedly, with the number of different numbers being the greatest common divisor of the numbers of the two different kinds of side!
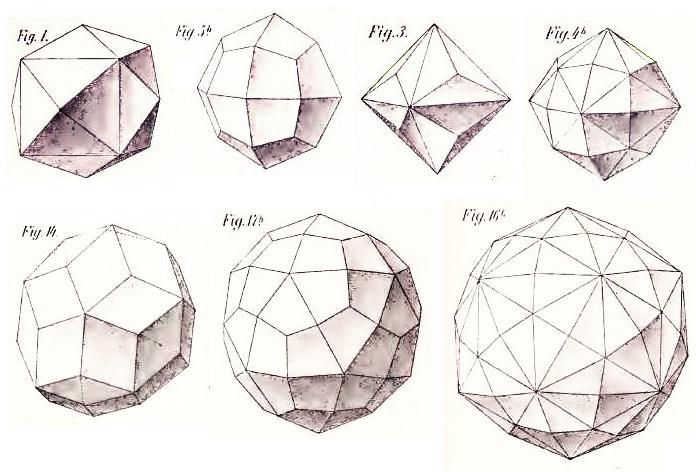
As for the Archimedian duals, here is an illustration of some of the Archimedian duals that have been used for dice:

In the top row, the most common d24, the Tetrakis Hexahedron, followed by a better d24, the Deltoidal Icositetrahedron. And then another possible twenty-four sided die, although not one I would recommend, the Triakis Octahedron. And the fourth shape is the Disdyakis Dodecahedron; this name is given to it because of its relationship to the rhombic dodecahedron. (It could also be called the Hexakis Octahedron.) This is the shape that has been used to make a d48.
In the bottom row is the d30, the Rhombic Triacontahedron, followed by the most common form of the d60, the Deltoidal Hexecontahedron, and the shape used to make a d120, the Hexakis Icosahedron (which could also be called the Disdyakis Triacontahedron).
It was in 1985 that the Zocchihedron was made available by GameScience. This was a die with 100 faces; this die did not have the perfect symmetry required for an assurance of fairness, but this slight imperfection could be a small price to pay for some for the convenience of having a single die to roll for a number from 1 to 100.
Initially, there were problems, though, with its distribution of numbers, and so an improved version was developed.
Also, since a nearly spherical die would likely roll too readily and too far to be convenient for use, this was combatted by having freely-moving weights inside the die to absorb energy as it rolled.
Incidentally, I noticed that while it was difficult to find any nearly symmetric arrangement for the faces on a 100-sided die, there was a good solution for a 200-sided die; here is a drawing of what I've come up with:
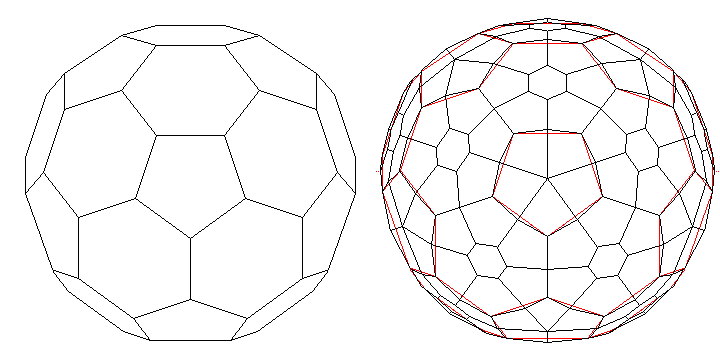
The d200 itself is sketched on the right; on the left, for comparison, is the truncated icosahedron on which its design is based.
Of course, with that many sides, no doubt it will be difficult to tell which one is on top! Of course, it may be possible to come up with a contrivance to deal with it: for example, have the d200 made as a transparent plastic hollow shell, with black numbers printed on it; fill it with water colored with black ink, but have a hollow white ball floating in that water, which will find its place under the topmost face, highlighting its numbers as the most visible! Think of it as a Magic 8 Ball turned inside-out?
Incidentally, while I couldn't think of a way to devise a d100 that was significantly better than the Zocchihedron, I've since learned of a discussion involving the noted mathematician John Horton Conway, inventor of the game of Life and the creator of the Somap which showed the relations between all but one solution of Piet Hein's Soma cube in which he pointed out a good possibility.
One hundred is four times twenty-five. A tetrahedron has four sides, and a triangle can be easily divided into a square number of smaller triangles.
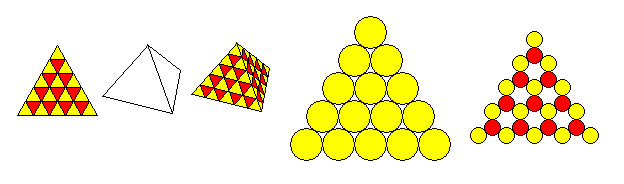
However, there is one issue with this shape, which is illustrated in the diagram above.
Two consecutive triangular numbers, added, make a square number, and so as the triangle on the left in the diagram above shows, 15 triangles pointing up, and 10 triangles pointing down, together fill one equilateral triangle with 25 triangles within it, the square number desired.
Combine such a triangle with a tetrahedron, and one gets a tetrahedron covered with 100 triangles. This can then be mapped to a sphere in some fashion, as a guide to where to put the faces of a 100-sided die.
But then we see that while triangular numbers correspond to a close packing of circles within a triangle - because the circles are allocated hexagonal areas, and a hexagon is close to a circle... when we instead place the circles corresponding to all the triangles in a packing of triangles within another triangle, because triangles are more pointy... some space has to be left unused.
So while a d100 based on Conway's suggestion would have a much more regular overall pattern than that of the Zocchihedron, if it was made of flat circular faces on a sphere (as is the Zocchihedron), then the circles would have to be smaller than those of the Zocchihedron. On the other hand, if we made the faces irregular triangles, that would help (slightly) with the problem of the die being too inclined to just keep on rolling, as a benefit of triangles being pointy.
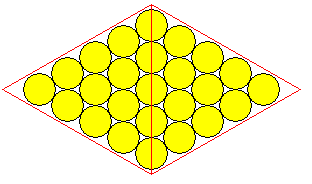
After looking for other possibilities, I realized that in addition to generating other possibilities by putting circles at all the vertices and along all the edges of a solid, thus filling the triangles with a number of circles belonging to an alternate series of triangular numbers, 4 1/2 circles, 8 circles, 12 1/2 circles, and so on, if I just took the circles on one edge of a triangle and put those on an edge of a solid, then an octahedron has four pairs of two faces, into which a hexagonally packed lozenge of circles containing 25 circles (or any other square number) would nicely fit, and so there is an improvement on the Zocchihedron which avoids a great amount of wasted space, by reasoning further from Conway's idea instead of only sticking with the most literal interpretation.
However, just because this structure is mathematically simple does not necessarily mean that it's really an improvement on the Zocchihedron. After all, a sphere is not a flat surface, so a triangle with circles in hexagonal close packing will have to be stretched considerably when placed on the sphere.
Each of what can be thought of as the Northern and Southern hemispheres of the Zocchihedron begins with one circle containing a number at one of its poles, surrounded by rings of circles with numbers, containing 6, 11, 15, and 17 circles in them.
These rings would be at 70, 50, 30, and 10 degrees of latitude respectively.
From this short table, we can see how well this choice of numbers for the rings fits the size of each ring, thus giving an equal amount of space on the die for each number:
6 / cos(70°) 17.54283 11 / cos(50°) 17.11296 15 / cos(30°) 17.32051 17 / cos(10°) 17.26225
So the fit is indeed very good, for 49 circles in four bands below one circle at the pole.
For comparison, the octahedral design above could be assessed on the basis:
4 / cos(80°) 23.03508 8 / cos(60°) 16 12 / cos(40°) 15.66489 16 / cos(20°) 17.02684 20 20
which is not nearly as regular.
But what would be desirable would be to have a higher level of symmetry; not just two hemispheres, or four quadrants, but ideally a die that could be divided into a larger number of identical pieces.
An icosahedron has 20 faces, and 100 is five times 20. But there is no symmetrical way, and not even any compact way, of fitting five circles into a triangle.
However, while the icosahedron has 12 vertices, it has 30 edges, and 30 is at least a multiple of 10.
Basing an arrangement of circular dimples on a die on this placement of circles on an icosahedron
would mean that there were four dimples for each of the 20 faces of the icosahedron, for a total of 80, plus one dimple for each of the 30 edges of the icosahedron, for a grand total of 110 dimples.
Now is there any tidy way to omit ten of them? Or could we just re-roll in the ten cases where a single digit came up, with a guarantee that only a single re-roll would ever be needed?
Because there are no dimples corresponding to the twelve vertices of the icosahedron, this arrangement of dimples isn't as even as it looks. So if a good d110 were desired, the dimples would have to be made a little smaller - with the centers of most of them staying where they are, but the dimples in the corners of the triangles moved further into the corners, to balance out the absence of dimples in the vertices.
Does acknowledging this fact help us arrive at ideas for making a good d100 out of this?
One thing I could come up with is illustrated above. There are 30 dimples on the edges, one on each. Half the triangles have four dimples, with the outer three shoved into the corners, and the other half have three dimples, closer to the center of the triangle, to balance the abscence of a dimple in the center of those triangles.
The top and bottom caps of the icosahedron each have two triangles with four dimples and three with three dimples, while each of the two layers of the central band have three triangles with four dimples and two triangles with three dimples.
That gives the shape as a whole 100 dimples to put on the sphere, and the dimples are located so as to be in opposing pairs around the center of the sphere, allowing for one dimple to be always the topmost face when rolled.
But this shape is also inferior to the Zocchihedron in that there are obvious large variations in the density of the dimples on the sphere.
 |
The image above is from Wikimedia Commons, licensed under the Creative Commons Attribution Share-Alike 4.0 International License, and is thus available for your use under the same terms. Its author is Saharasav. |
A very unusual die is the d34, which, like the d10 and d14, is made from trapezoids so that when one of the seventeen kite shapes is resting, another one is face up. Three such dice, numbered from 1 to 34, give a total from 3 to 102, and so if one subtracts 2 from the total, one has a number from 1 to 100, with a normal distribution. Just as three six-sided dice, giving a total from 3 to 18, are used for generating character attributes in games that make frequent use of the twenty-sided die (d20), one game that used the d100 instead had based character generation on 3d34.
The game Realms of Adventure by James Patrick Updike used 3d34 for generating character attributes like this, so there is at least one actual example. (While the game is still available from DriveThruRPG, and at a low price for the PDF, the domain for the game's own web site has lapsed, I have noticed.) I've also learned that these dice were manufactured by Chessex. Also, I've found an image of such a die that I can use, and it is visible to the right.

I had thought some other, more well-known game also did so, and I have a vague memory of seeing them associated with a game the packaging of which reminded me of the science-fiction RPG Traveller. (More recently, I've seen a d50 of this same form offered for sale by Gamescience for use with that RPG; perhaps I saw it before, and that's what confused me. A specimen of this d50 is now shown at left.) RuneQuest is a well-known RPG that uses a d100 system, unlike the d20 system used by certain editions of Dungeons and Dragons, but it uses 3d6, and not 34-sided dice, for character generation.
Basically, 3d34 minus 2 totals are symmetric with respect to d100, while 3d6 without modification is symmetric with respect to d20.
It is also true that 3d8 minus 1 is symmetric with respect to d24. While d24 isn't one of the original RPG dice shapes, it's commonly enough available and well-known now. However, d30 is considerably more commonly available, at least in my own personal experience, and 3d10 minus one is symmetric with respect to d30. [Yes, it's the OGL controversy of January, 2023 that led me to consider such alternatives.]
What can one do if one doesn't have a d34 available?
My first thought was to use 2d36 plus d30; two more twice, plus four less once. One would use two ordinary d6 dice of different colors for the d36, of course.
Another possibility would be to roll 3d6, multiply the result by five (to convert from the d20 realm to the d100 realm, of course), and then, to allow in-between numbers, add the result of rolling 2d6. Then subtract 9 from the result to give it the desired symmetry around the midpoint between 50 and 51.
For comparison: the range of 3d34 minus 2 is 1 to 100 exactly; the range of 2d36 plus d30 minus 2 is also 1 to 100 exactly; but the range of 5 times 3d6 plus 2d6 minus 9 is 8 to 93, so the seven lowest numbers and the seven highest numbers are lost.
Further thought led me to modify this a bit: roll 3d6, and multiply the result by six. This would produce a number from 18 to 108. Add the result of 2d6 to that, and the result is a number from 20 to 120, and so subtracting 20 produces a number from 0 to 100 which is in an approximation to a normal distribution - the general outline would be like a normal distribution, but straight lines would connect the probabilities of rolls of the form 6n-2.
The amount of arithmetic to be done could be reduced by using special dice. For example, one could roll two dice numbered from 0 to 5, and three dice numbered from 0 to 30 in steps of 6.
Another option has occured to me. 3d30 produces sums that go from 3 to 90. If one rolls 3d30 to get the overall bell curve, and also 2d6 to widen it a bit, the total of all these dice will range from 5 to 102. Subtract 3, and the range will be from 2 to 99, thus properly centered halfway between 50 and 51, and only omitting the largest and smallest number.
While this will have a somewhat lower probability of producing results at the extreme ends than 3d34 minus 2, it will certainly produce a closer distribution than the suggestion advanced by the rules for Realm of Adventure for what to do if a d34 is not available: just use a d100!
Another option that might have occured to some gamers in this situation would be to roll 5d20. 5d20 minus 2 has a range of 3 to 98. But with five dice of equal size, there would be more of a tendency for the rolls to average out, and so the distribution of results around the central peak would be significantly narrower.
What about rolling three dice, and taking the number on the one that is in the middle? It turns out that while the probability distribution of this is a curve that is the highest in the middle, that curve is more like a semicircle than a bell curve, so the chance of results far from the mean is still considerably higher, and even higher than from rolling two dice. But if you take the middle die of five dice, you get something closer to a bell curve, although still not quite as tapered on the ends. Which, of course, may not be a bad thing, as it makes it more likely to generate heroic characters.
And many RPG players would be far more likely to have five d100s than even one d34.
And at this point, I should give thanks to AnyDice.com, which makes it easy to examine the distribution of the results from such possibilities.
Incidentally, the d50 is also known as the "Danish Lottery Die" (and this term has also been used for the d34, I suspect mistakenly), as it apparently was originally made to help people pick numbers to play in a lottery in Denmark. Checking into this, I have found there currently is played a lottery exclusive to Denmark, just called Lotto, involving the numbers from 1 to 36, and another lottery, Euro Jackpot, played in a number of northern European countries, including Denmark, that does involve the numbers from 1 to 50. There's also Vikinglotto, using the numbers from 1 to 48.
I am not quite sure, just yet, where to look to find information on historical lotteries that used to be played in Denmark; this is probably where the true application of such dice would be found.
I thought I would take a moment to consider advancing another step in this progression. A d1000 can be obtained through the use of three distinct d10 dice easily enough.
If one wanted an odd number of possibilities, 1001 is 7 times 11 times 13. So one could use a d14, a d22, and a d26, suitably labelled with numbers.
The d14 would be labelled with the numbers 0, 1, 2, 3, 4, 5, 6 twice.
The d22 would be labelled with the numbers 0, 7, 14, 28, 35, 42, 49, 56, 63, 70 twice.
The d26 would be labelled with the numbers 0, 77, 154, 231, 308, 385, 462, 539, 616, 693, 770, 847, 924 twice.
Replacing the d11 and d13 with two d12s would give 144 possibilities instead of 143 possibilities, and so one would only have to re-roll if both dodecahedral dice came up with their highest faces.
In that case, the d14 would again be labelled with the numbers 0, 1, 2, 3, 4, 5, 6 twice.
The first d12 would be labelled with the numbers 0, 7, 14, 28, 35, 42, 49, 56, 63, 70, 77 and this time each number would only occur once.
The second d12 would be labelled with the numbers 0, 84, 168, 252, 336, 420, 504, 588, 672, 756, 840, 924 again once.
And so the two d12s would be rerolled if 77 and 924, which total to 1001, came up on them. Otherwise, the three dice would give a number from 0 to 1000.
So for stats, one would roll 2d334 + d335 - 3 to get a number from 0 to 1000. The trouble is...
333 = 3 * 3 * 37 334 = 2 * 167 335 = 3 * 3 * 67 336 = 2 * 2 * 2 * 2 * 3 * 7
Both a d334 and a d335 are wholly impractical, and so is a d333. However, a d14 and a d24 can work together to form a d336.
If the d24 continues to be labelled with the numbers from 1 to 24, the d14 can be labelled with the numbers 0, 24, 48, 72, 96, 120, 144, 168, 192, 216, 240, 264, 288, 312 once.
So let's give up our plans to use a d1001, and stick with the d1000, and roll stats with 3d336 - 5 to get a number from -2 to 1003 with a bell curve distribution!
Today, the mass manufacture of polyhedral dice has made them economical, with pre-painted numerals standard. The edges are more rounded, and harder plastics, similar to those used for ordinary dice, are employed in their manufacture.
Before proceeding, it will be helpful to look at some more pictures of actual dice in the unusual shapes we have been discussing, and that we will be discussing later at greater length.