As noted on the previous page, the Archimedian duals, or Catalan solids, are the following, sorted by number of faces:
Using, once again, Vielecke und Vielflache by Dr. Max Brückner as our source for the drawings used here, here are illustrations of all the Archimedian duals together with the Archimedian solids on which they are based.
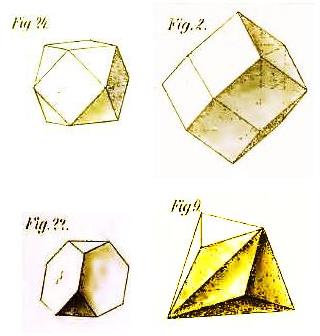
First, the two Archimedian duals with 12 faces:

In the first row is the cuboctahedron, followed by its dual, the rhombic dodecahedron.
In the second row is the truncated tetrahedron, followed by its dual, the triakis tetrahedron.
Next, the Archimedian duals with 24 faces:
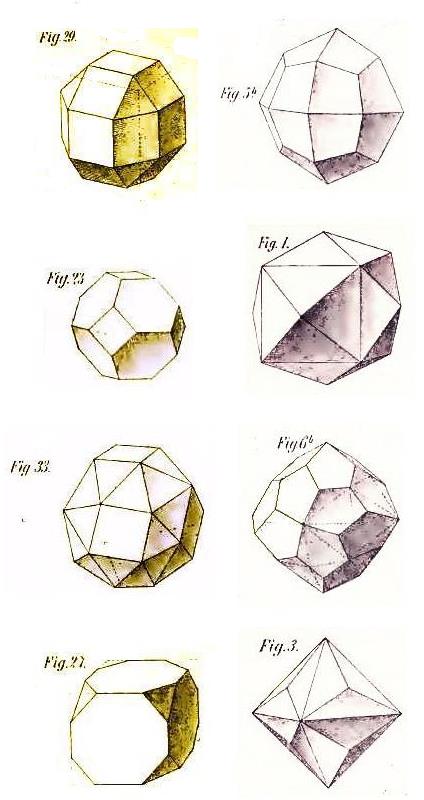
In the first row is the small rhombicuboctahedron, followed by its dual, the deltoidal icositetrahedron.
In the second row is the truncated octahedron, followed by its dual, the tetrakis hexahedron.
In the third row is the snub cube, followed by its dual, the pentagonal icositetrahedron. Note that these solids both come in two forms with opposite parity: now that I have checked, it appears that the two drawings are of the corresponding forms of these solids.
In the fourth row is the truncated cube, followed by its dual, the triakis octahedron.
And now the one Archimedian dual with 30 faces:
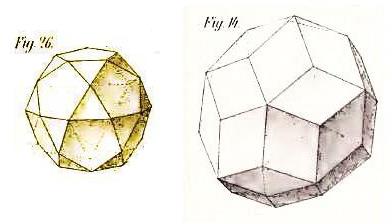
This image shows the icosidodecahedron, followed by its dual, the rhombic triacontahedron.
And now the one Archimedian dual with 48 faces:
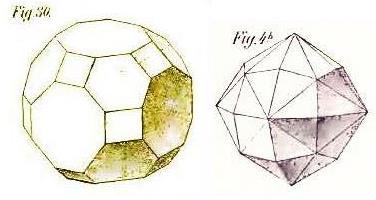
This image shows the great rhombicuboctahedron, also known as the truncated cuboctahedron, and its dual, the disdyakis dodecahedron. Note that this Archimedian dual is the disdyakis solid derived from the rhombic dodecahedron, and that it could also be termed the hexakis octahedron.
Next, the Archimedian duals with 60 faces:
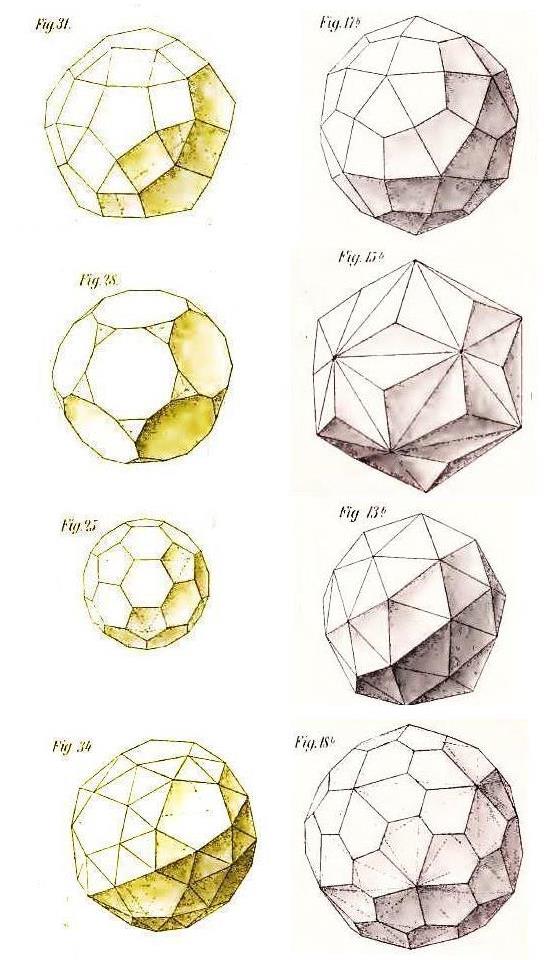
In the first row is the small rhombicosidodecahedron, and its dual, the rhombic hexecontahedron.
In the second row is the truncated dodecahedron, and its dual, the triakis icosahedron.
In the third row is the truncated icosahedron, and its dual, the pentakis dodecahedron.
In the fourth row is the snub dodecahedron, and its dual, the pentagonal hexacontahedron. Note that these solids both come in two forms with opposite parity: now that I have checked, it appears that in this case, the two drawings are not of the corresponding forms of the solids involved, but instead each one is of the opposite parity to that of the dual of the other one.
And finally, the one Archimedian dual with 120 faces:
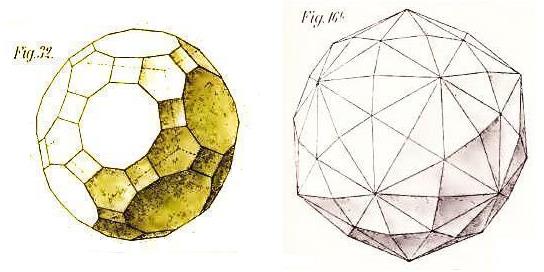
This image shows the great rhombicosidodecahedron, also known as the truncated icosidodecahedron, and its dual, the disdyakis triacontahedron, which could also be termed the hexakis icosahedron or the dekakis dodecahedron.