At least one firm makes available a d24, made from four shallow pyramids on each face of a cube (one could put the pyramids on the faces of an octahedron, or rotate those on the face of the cube by 45 degrees each as alternatives), a d14, a trapezohedron based on seven-sided pyramids instead of five-sided ones, and a d16 made from two eight-sided pyramids joined without a twist.
An alternate possibility for the d12 is the rhombic dodecahedron; this was used at least once for a set of astrology-based fortune-telling dice, called "Ask Astro-Dice", and apparently only offered for sale for a brief time around 1978. A rhombic dodecahedron looks like this:

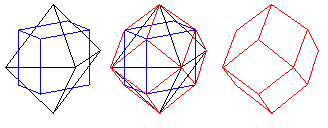
as can be seen from the diagram, it is closely related to the cube and the octahedron. It can be thought of as a cube with pyramids on each of its faces, or an octahedron with pyramids on each of its faces, high enough in both cases that the triangular sides of adjoining pyramids unite to form a diamond shape.
A d24 could be made by reducing the height of these pyramids to about half of what is required to form the rhombic dodecahedron in either case, and as noted, this has been done for the cube, but not the octahedron.
Below is an image of the shape of the most commonly available type of d60, a deltoidal hexecontahedron, from a book published in 1900 (Vielecke und Vielflache by Dr. Max Brückner),
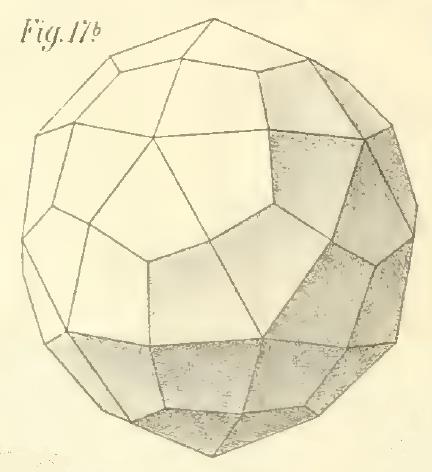
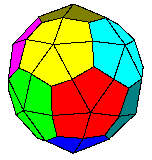
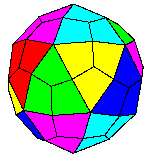
and because I am lazy, I have used that image as the basis for the two diagrams which follow, showing how the dodecahedron and the icosahedron are both manifest within that shape.
The availability of unusual dice seems to be increasing of late. Alternate forms of the d24 are available.
Gamescience makes available a set of dice, called the Zocchi Pack, including three otherwise hard-to-find dice of the kinds mentioned above, the d14, d16, and d24, along with a d3 and a d5. The d3 is a rounded shape based on a prism; the d5 is a triangular prism which also uses its top and bottom as possible faces.
Koplow Games makes available a set of special dice called "Who Knew?" that includes a d3, d5, d7, d16, d24 and d30. The unusual shapes for the d3, d5, and d7 are avoided by instead creating a d3, d5 and d7 by repeating the numbers from 1 to 3, from 1 to 5, or from 1 to 7 respectively twice on a d6, a d10, and a d14. The d14 has the same category of trapezohedral bipyramidal shape as the d10.
From Genomic Games, a set is available that consists of a d3, d5 and d7 of the type noted above for Koplow's offering, and a d14, d16, d24, and d30. Except that some people may already have a d30, since it also includes the d14, it more closely matches what many people will be looking for.
Chessex, another major supplier of game dice, makes individual dice of these shapes, but does not offer a packaged set.
I've also seen a site on the web indicating that a set of ordinary RPG dice that adds a d24 and a d30 to the usual set is available for import from China.
On the other hand, I've heard reports that the d30 is becoming hard to find again.
The d3, d5, d7, d14, d16, and d24 have started to become available in response to these dice being used in the RPG Dungeon Crawl Classics, made by Goodman Games. As they note on their site, the game module #36, Talons of the Horned King, was the first one to make use of these additional dice. This module was first published in 2006.
For that matter, I've also seen pictures of an alternate d4 made by repeating the numbers from 1 through 4 twice on a d8; as well, Chessex makes dice they call "Roman Dice", which are dodecahedrons (d12) with the numbers from 1 through 4 printed on them three times. If this means that the octahedron is so pointy that, although it rolls more easily than a tetrahedron, it still leaves something to be desired, I suppose it's only a matter of time before someone makes a bipyramidal d16 with the numbers 1 through 8 repeated twice as an alternative form of d8, although I think that a trapezohedral d24 with those numbers repeated three times would be a better idea.
Personally, I feel that one option that hasn't been explored would be to make an octahedral d8 where the triangular faces are replaced by circular faces, touching each other on what is otherwise a sphere. After all, at one time ordinary six-sided dice, on which the corners were so rounded that the die was a sphere with six circular faces, were common, usually made in China.
This would roll more before coming to a stop, so that the fact that the corners of an octahedron are... pointier... than the corners of a cube would no longer be a problem.
Repeating the numbers from 1 to 4 twice on this kind of octahedral die would completely solve the d4 problem as well.
While I don't have any better solutions than the existing trapezohedral bipyramid and regular bipyramid for the d14 and d16 respectively, one can make a d15 by repeating the numbers from 1 to 15 twice on a rhombic triacontahedron.
So there you have it, my ideas for making an ideal set of dice for role-playing games.
Thus, the diagram below sums up the history of the development of dice for role-playing games:
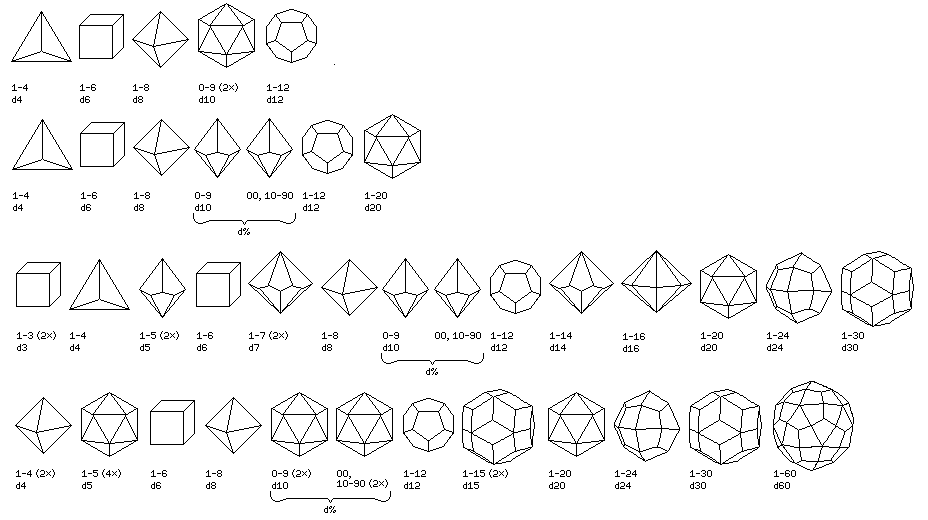
In the first line is the original set used with Dungeons and Dragons: five dice, corresponding to the Platonic solids, with the icosahedral die marked with the numbers 0 through 9 repeated twice each.
In the second line is the usual set used today: the icosahedral die is marked with the numbers 1 through 20, to be a true d20, and a pair of ten-sided dice in the shape of twisted bipyramids is used to allow numbers from 1 to 100 to be rolled, with tens being marked explicitly on the tens dice.
In the third line, the expansion of the set of dice used in the game Dungeon Crawl Classics is shown in one possible implementation, in line with my preference for obviously fair dice whenever possible (i.e. using a twisted bipyramidal die for the d14, and a bipyramidal die for the d16) and for the d24 based on the Deltoidal Icositetrahedron instead of the d24 based on the Tetrakis Hexahedron.
Then in the fourth line, to keep the image from becoming too wide, I omit most of the additional DCC dice, keeping only the d5, for which I have a preferred alternate form that is less common, showing the forms I prefer for the d4, the d5, and the d10, as well as adding the d60, as this is readily available, and the d15 derived from the d30 by using the numbers from 1 to 15 twice, which, as far as I know, is not yet available anywhere. Thus, I use Platonic solids or Archimedian duals wherever possible, only using bipyramids for the d7, the d14, and the d16, as these genuinely fair dice are my second preference.
It's also possible to obtain hollow transparent dice with an additional die inside. The dice are of the same shape; maybe someday, someone is going to put a d30 inside a d24, or vice versa, to create a die that can simulate all the other common shapes, as well as one uncommon one, easily:
d24 | d4 d6 d8 d12 (d20) (2d12) | d30 | d6 d10 (d16)
-----------------------------------------------------------------------
1 | 1 1 1 1 0 0 | 1 | 1 1 0
2 | 2 2 2 2 +10 +6 | 2 | 2 2 +8
3 | 3 3 3 3 0 0 | 3 | 3 3 0
4 | 4 4 4 4 +10 +6 | 4 | 4 4 +8
5 | 1 5 5 5 0 0 | 5 | 5 5 0
6 | 2 6 6 6 +10 +6 | 6 | 6 6 +8
7 | 3 1 7 7 0 0 | 7 | 1 7 0
8 | 4 2 8 8 +10 +6 | 8 | 2 8 +8
9 | 1 3 1 9 0 0 | 9 | 3 9 0
10 | 2 4 2 10 +10 +6 | 10 | 4 0 (10) +8
11 | 3 5 3 11 0 0 | 11 | 5 1 0
12 | 4 6 4 12 +10 +6 | 12 | 6 2 +8
13 | 1 1 5 1 0 +6 | 13 | 1 3 0
14 | 2 2 6 2 +10 0 | 14 | 2 4 +8
15 | 3 3 7 3 0 +6 | 15 | 3 5 0
16 | 4 4 8 4 +10 0 | 16 | 4 6 +8
17 | 1 5 1 5 0 +6 | 17 | 5 7 0
18 | 2 6 2 6 +10 0 | 18 | 6 8 +8
19 | 3 1 3 7 0 +6 | 19 | 1 9 0
20 | 4 2 4 8 +10 0 | 20 | 2 0 (10) +8
21 | 1 3 5 9 0 +6 | 21 | 3 1 0
22 | 2 4 6 10 +10 0 | 22 | 4 2 +8
23 | 3 5 7 11 0 +6 | 23 | 5 3 0
24 | 4 6 8 12 +10 0 | 24 | 6 4 +8
25 | 1 5 0
26 | 2 6 +8
27 | 3 7 0
28 | 4 8 +8
29 | 5 9 0
30 | 6 0 (10) +8
A d20 is achieved by adding the (d20) number to the d10 number from the d30 (counting 0 as 10), and a second d12 is achieved by adding the (2d12) number to the d6 number from the d30. A d16 can be achieved by adding the (d16) number to the d8 as well. Since both dice can simulate a d6, 2d6 is also available.
Other arrangements for the (2d12) column are possible, as long as for each number from 1 to 12 in the d12 column, one occurrence corresponds to a 0, and the other occurrence corresponds to a +6. The most obvious arrangement would have been 12 zeroes followed by 12 instances of +6.
On further reflection, I've realized that dice with fewer sides could be used successfully. A d20 inside a d6, for example, would also be able to simulate the other common die sizes, and not only that, for the most part the rolls could be derived fairly easily in one's head, without recourse to tables:
d4 d6 is ODD: 1 d6 is EVEN: 2 d20 is EVEN: +2 d8 d6 is EVEN: +4 d20 1 5 9 13 17 | 1 2 6 10 14 18 | 2 3 7 11 15 19 | 3 4 8 12 16 20 | 4 d10 d6 - ignore d20 - use the last digit d12 d6 - use the number rolled d20 is EVEN: +6
Only the d8 requires a slightly difficult task, determining the residue class modulo 4 (or, less technically, the remainder after division by 4) of the number rolled on the d20. Still, many people are well-practiced in mental division by 4 in order to determine leap years, so it's not too bad.
One way to simplify this would be to underline all the numbers that go to 1 and 2 in the table shown above for interpreting the d20 in calculating a d8 result: not just 9, but also 1, 5, 13, and 17; not just 6, but also 2, 10, 14, and 18.
Then the rule becomes:
ODD and underlined: 1 EVEN and underlined: 2 ODD and plain: 3 EVEN and plain: 4
Of course, since an icosahedral d20 has triangular faces, underlining the 6 and 9 to avoid ambiguity is not strictly necessary, as the convention that an apex of the triangular face is the 'top', and a side is the 'bottom', but this does make use of a very simple special marking that already has a reason to be present, and falls short of the complexity found on the D-Total.
Still further reflection has brought me to realize that with a bit more imagination and flexibility, there is a way to easily use a d20 as a d4 without the need for special markings.
In addition to distinguishing between even (pair) and odd (impair) at a glance, one can also distinguish between high (passé) and low (manqué) at a glance, where the numbers from 1 to 9, and also 20, are taken as "low", and the numbers from 10 to 19 are taken as "high".
Odd and Low: 1 Even and Low: 2 Odd and High: 3 Even and High: 4
While it would be possible to make a conversion table for simulating the rolls of other combinations of dice through the use of three six-sided dice, it does have to be admitted that it is easier to use three ten-sided dice of different colors, used as a d1000, for this purpose.
The chart below shows the proportionate probabilities for the totals produced by various dice combinations often used for weapons damage, the effects of healing spells, and the like:
1d4 2d4 3d4 4d4 5d4
1 1 .250
2 1 .500 1 .063
3 1 .750 2 .187 1 .016
4 1 1.0 3 .375 3 .063 1 .004
5 4 .625 6 .156 4 .020 1 .001
6 3 .813 10 .313 10 .059 5 .006
7 2 .937 12 .500 20 .137 15 .021
8 1 1.0 12 .687 31 .258 35 .055
9 10 .844 40 .414 65 .118
10 6 .937 44 .586 101 .217
11 3 .984 40 .742 135 .349
12 1 1.0 31 .863 155 .500
13 20 .941 155 .651
14 10 .980 135 .783
15 4 .996 101 .882
16 1 1.0 65 .945
17 35 .979
18 15 .994
19 5 .999
20 1 1.0
1d6 2d6 3d6 4d6 1d8 2d8 3d8
1 1 .167 1 .125
2 1 .333 1 .028 1 .250 1 .016
3 1 .500 2 .083 1 .005 1 .375 2 .047 1 .002
4 1 .667 3 .167 3 .019 1 .001 1 .500 3 .094 3 .008
5 1 .833 4 .278 6 .046 4 .004 1 .625 4 .156 6 .020
6 1 1.0 5 .417 10 .093 10 .012 1 .750 5 .234 10 .039
7 6 .583 15 .162 20 .027 1 .875 6 .328 15 .068
8 5 .722 21 .259 35 .054 1 1.0 7 .437 21 .109
9 4 .833 25 .375 56 .097 8 .563 28 .164
10 3 .917 27 .500 80 .159 7 .672 36 .234
11 2 .972 27 .625 104 .239 6 .766 42 .316
12 1 1.0 25 .741 125 .336 5 .844 46 .406
13 21 .838 140 .444 4 .906 48 .500
14 15 .907 146 .556 3 .953 48 .594
15 10 .954 140 .664 2 .984 46 .684
16 6 .981 125 .761 1 1.0 42 .765
17 3 .995 104 .841 36 .836
18 1 1.0 80 .903 28 .891
19 56 .946 21 .932
20 35 .973 15 .961
21 20 .988 10 .980
22 10 .996 6 .992
23 4 .999 3 .998
24 1 1.0 1 1.0
To avoid using excessive space, only the most common combinations are listed here, but this file contains a more extensive table of similar information, for dice from two to twenty sides.
The ancient Romans sometimes used dice in the shape of a cuboctahedron; this shape had fourteen sides, being a cube cut down on the corners so that a square in diamond orientation was left of each square face, with a triangular face on each of the eight corners.
Eight and six are both even numbers, so one could mark half of the faces of each kind "E" and the other half "O", and have a fair d2 despte the probability of landing on a square face versus a triangular face being unknown.
Similarly, the truncated icosahedron, the Archimedian solid with flat hexagonal and pentagonal faces corresponding to the arrangement of curved white and black segments on a modern soccer ball, has 20 hexagonal faces and 12 pentagonal faces. Both 20 and 12 are divisible by 4, so one could make a fair d4 from this shape.
If one started with the 30-sided rhombic triacontahedron, and, at the places where the obtuse angles of three diamonds met, cut an equal amount off each place, to add twenty triangular faces, then one would have a solid with thirty identical faces that were elongated hexagons, and twenty identical faces that were equilateral triangles.
So this solid with fifty sides could be used as a fair d10.