Since the Archimedian solids are bodies for which every corner is identical, their duals will have faces which, although not regular polygons, are all identical. This will, for one thing, make them (in most cases) possible shapes for dice. Indeed, we saw the rhombic triacontahedron on the preceding page, which is used for the d30.
Archimedian duals are not the only possible shapes for dice in addition to the Platonic solids, as I note on this page. There are also the bipyramids, and one class of trapezohedra, the duals of the antiprisms.
The dual of the truncated tetrahedron is the triakis tetrahedron, which looks like a tetrahedron with a shallow triangular pyramid on each of its faces. While this has 12 identical faces, like the tetrahedron itself, the faces are not in opposite pairs, and so one would choose a different solid with 12 faces for a 12-sided die.
Similarly, the dual of the truncated cube is the triakis octahedron, an octahedron with a shallow triangular pyramid on each of its faces. This could be used as a 24-sided die, but the triangles are quite elongated.
And the dual of the truncated dodecahedron is the triakis dodecahedron, an icosahedron with a shallow triangular pyramid on each of its faces. It could be used as a 60-sided die, but again, the faces are very elongated triangles, and there are other choices.
Also similarly, the dual of the truncated octahedron is the tetrakis hexahedron, a cube with a shallow square pyramid on each of its faces. This is the shape most commonly used for a 24-sided die, as it is simple to understand, although, as the triangular faces are elongated, a better option exists.
As well, the dual of the truncated isosahedron is the pentakis dodecahedron, a dodecahedron with a shallow pentagonal pyramid on each of its faces. Here, the triangles are not far from equilateral, so it is a reasonable choice for a 60-sided die.
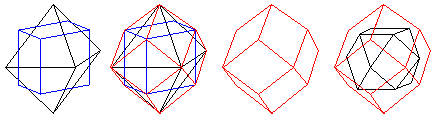
The dual of the cuboctahedron is the rhombic dodecahedron. This 12-sided shape, with its symmetrical diamond-shaped faces, has been used as a 12-sided die. It is related both to the triakis octahedron and the tetrakis hexahedron, since it could be formed by raising the pyramids in either one so that pairs of triangles from two adjacent pyramids became single diamond-shaped faces.
The image below shows how it is related to the cube and the octahedron, in addition to showing the cuboctahedron.

Similarly, the dual of the icosidodecahedron is the rhombic triacontahedron. This is the shape used for the d30. It can be derived from raising the pyramids on either the triakis icosahedron or the pentakis dodecahedron.
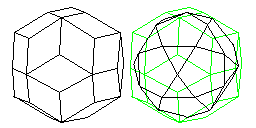
The dual of the small rhombicuboctahedron is the deltoidal icositetrahedron. Sometimes it is also called the trapezohedron. This 24-sided solid, with its kite-shaped faces, is the best choice for a die with 24 faces.
Similarly, the dual of the small rhombicosidodecahedron is the deltoidal hexecontahedron. This 60-sided solid is another good choice for a 60-sided die, and indeed this is the shape commonly used for the commercial d60.
The dual of the truncated cuboctahedron, or the great rhombicuboctahedron, is the disdyakis dodecahedron. This solid has 48 triangular sides. However, the sides are not all identical; instead, they are in two groups of 24, with those in one group being mirror reflections of the other group. A shallow pyramid with a diamond-shaped base can be placed on each face of a rhombic dodecahedron to form this solid.
The dual of the truncated icosidodecahedron, or the great rhombicosidodecahedron, similarly, is the disdyakis triacontahedron. This solid has 120 triangular sides. Again, they come in mirror-reflected pairs. The solid can be formed by placing a shallow pyramid with a diamond-shaped base on each face of a rhombic triacontahedron.
The dual of the snub cube is the pentagonal icositetrahedron, with 24 sides, which like its dual exists in two forms with opposite parity.
Similarly, the dual of the snub dodecahedron is the pentagonal hexecontahedron, a 60-sided solid which exists in two forms with opposite parity.
So far, I have only included two images of an Archimedian dual, these being more difficult to draw. However, I have found an old book with reasonably good images that I can include, so here are the images from that source, the 1900 book Vielecke und Vielflache by Dr. Max Brückner, which I do not need to draw myself:
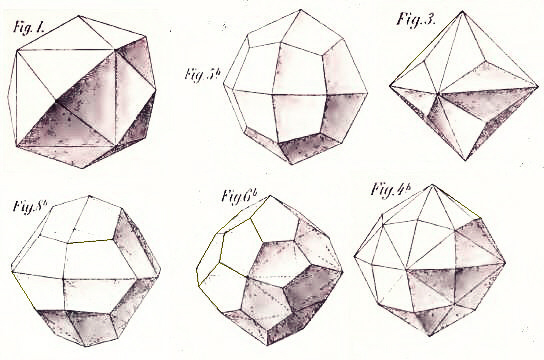
This image shows the Tetrakis Hexahedron, the dual of the truncated octahedron, with 24 faces, the Deltoidal Icositetrahedron, the dual of the rhombicuboctahedron, also with 24 faces, and the Triakis Octahedron, the dual of the truncated cube, also with 24 faces, in the top row, and a distorted Deltoidal Icositetrahedron, which is not an Archimedian dual, but is still an isohedron, that is, a shape that could be used for a fair die with 24 faces, the Pentagonal Icositetrahedron, the dual of the snub cube, also with 24 faces, and the Disdyakis Dodecahedron, the dual of the truncated cuboctahedron, with 48 faces in the bottom row.
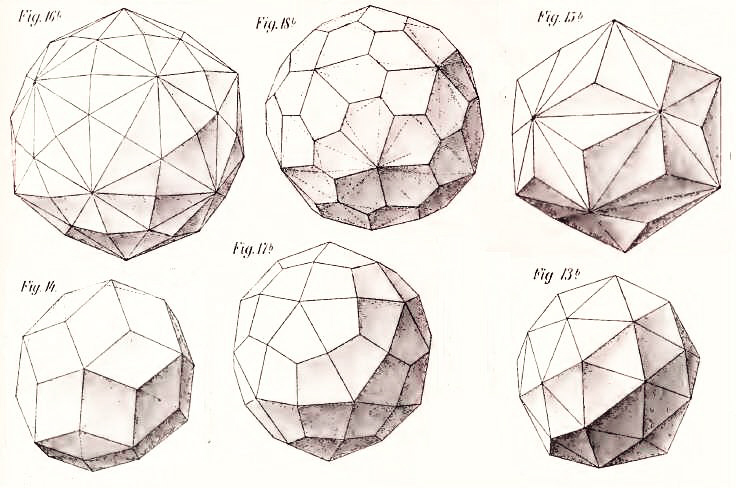
This image shows the Hexakis Icosahedron, the dual of the truncated icosidodecahedron, with 120 faces, the Pentagonal Hexecontahedron, the dual of the snub dodecahedron with 60 faces, and the Triakis Icosahedron, the dual of the truncated dodecahedron, also with 60 faces, in the top row, and the Rhombic Triacontahedron, the dual of the icosidodecahedron, with 30 faces, the Deltoidal Hexecontahedron, the dual of the rhombicosidodecahedron, with 60 faces, and the Pentakis Dodecahedron, the dual of the truncated icosahedron, also with 60 faces, in the bottom row.
Using that book again as the source for my images, on this page in another section of my site, I illustrate all the Archimedian duals, together with the solids of which they are the duals, in order by the number of faces on the dual.