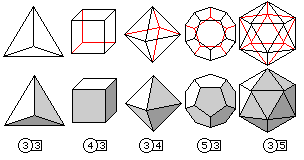
The five basic Platonic solids, the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, are illustrated in the diagram below.

After these, the most basic solid shapes, there is a family of shapes whose faces are regular polygons which is one step less uniform than them, known as the Archimedean solids. These bodies are those which may have more than one type of face, but which only have one kind of corner.
Some of the Archimedean solids can be formed by trimming off the corners of a Platonic solid. For example, we can start with a dodecahedron, and trim off its corners to change each face from a pentagon to a decagon, leaving an additional small triangular face at each corner. Or, we can trim more deeply, again having a triangular face where the corners of the dodecahedron were, but this time changing the pentagonal faces to smaller pentagons facing the other way.
The three solids this process will produce are the dodecahedron, a Platonic solid, and the two Archimedean solids known as the truncated dodecahedron and the icosidodecahedron.
Another shape, which could be obtained from a dodecahedron, is easier to obtain by this method by trimming the corners of an icosahedron, thus creating little pentagonal faces at each corner, and changing the triangular faces to hexagons.
This new shape is called the truncated icosahedron. And it is, of course, a familiar shape to soccer fans, since the pattern on most soccer balls is based on this solid, with the hexagons white and the pentagons black. But a soccer ball is still a sphere, not a polygon. It is also possible to trim off the corners more deeply, changing the triangles into triangles pointed the other way instead of to hexagons, and this is another way to obtain the icosidodecahedron.
Soccer balls did not always have this shape. The form of a soccer ball most familiar to me from my childhood was of a 12-panel ball, following the style used in the World Cup in Brazil in 1950. An 18-panel variation on this, where three segments side by side make up each unit corresponding to the faces of a cube, is said to be quite common, and a 12-panel ball where each panel was T-shaped was used in a number of the earliest World Cup matches; the Top Star ball used in the 1958 World Cup also had a shape reminiscent of this style, but as the "T" was split into two parts, it had 24 panels rather than 12.
The inventor of the soccer ball based on the truncated icosahedron is believed to be Eigil Nielsen, who designed it for the Select Sport company in Denmark in 1962.
While some sources I encountered initially credited Adidas with bringing in the white and black coloring scheme, others pushed that further back, possibly to 1965.
Thus, a variation of that style was already being in the European Cup for 1965, in which the soccer ball was made of pentagonal and triangular panels, after the manner of an icosidodecahedron, with the triangular panels white, and the pentagonal panels being white with a smaller black pentagon in the center, of precisely the same size as the pentagonal panel of a soccer ball patterned after the truncated icosahedron. And a ball of the white and black truncated icosahedral style was used in one of the semi-finals for the 1966 European Cup.
However, I have now encountered one web site with a photograph from the October 1963 issue of Football magazine showing a soccer ball of that pattern in use for a game between teams from France and the German Federal Republic played on October 24, 1962, and thus presumably it was Select Sport that originally offered that coloring scheme as an option.
Adidas began making soccer balls of this style in 1968, with the Telstar Elast; it was in 1970, however, when the Adidas Telstar was used for the 1970 World Cup that this style of soccer ball became well-known even in North America, and achieved near-universal dominance.
This style of ball was significantly closer to a perfect sphere than the previous style, and that contributed to its popularity. However, it is possible to have too much of a good thing: the Jabulani, used in the 2010 World Cup, was even closer to a perfect sphere; so much so that players complained of its erratic behavior.
The diagram below shows these shapes, starting from the dodecahedron on the left, proceeding to the truncated dodecahedron, the icosidodecahedron, then the truncated icosahedron, and finally the icosahedron.
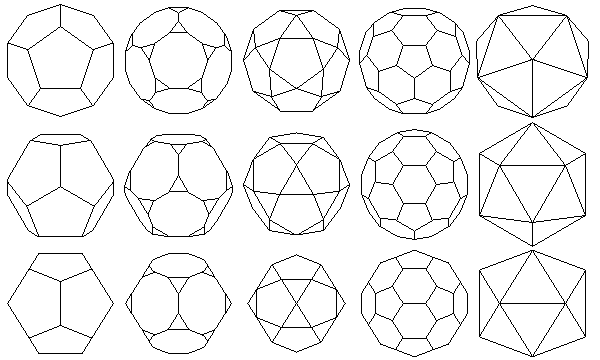
The solids are depicted three times; in the top row, they are viewed down an axis of fivefold symmetry, in the middle row, they are viewed down an axis of threefold symmetry, and in the bottom row, they are viewed down an axis of symmetry that makes plain their relation to the cube.
Replacing triangles by triangles pointed the other way or by hexagons, and stretching an edge so it becomes a square, we can derive two other Archimedean solids from the ones we have seen so far, as seen below:
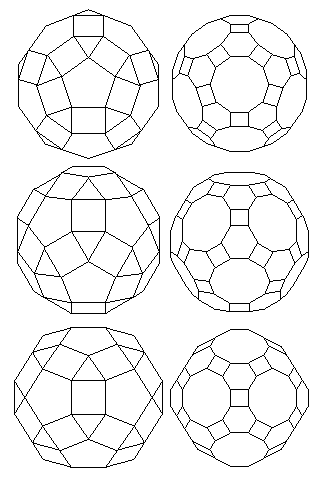
These solids are known as the small rhombicosidodecahedron and the great rhombicosidodecahedron. Once again, they are shown three times, in the top row from a direction of pentagonal symmetry, in the middle row along a direction of triangular symmetry, and in the bottom row along a direction of double bilateral symmetry.
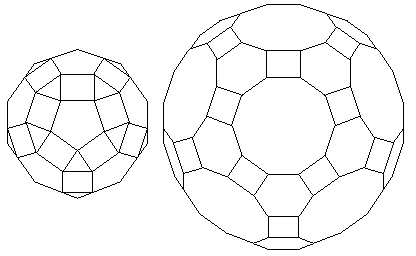
It is possible to draw the great rhombicosidodecahedron with the same size of side as the small rhombicosidodecahedron; in that case, a diagram such as the one below illustrates the reason behind their names:
Yet another solid belongs to this branch of the family of Archimedean solids, the snub dodecahedron. This one was, however, too hard for me to draw accurately using the technique I have been using for these diagrams. However, I was able to draw a picture of the surface of one in an unfolded state.
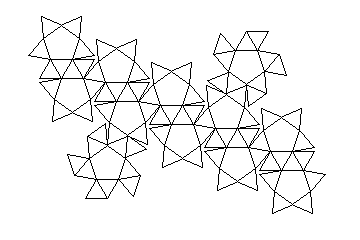
Since this page was originally created, I have finally decided to make the effort to produce a likeness of the snub dodecahedron in its solid glory as best I could:
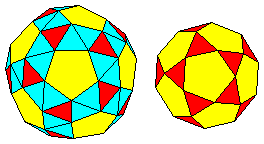
It is depicted beside an icosidodecahedron oriented so that the faces, colored red and yellow, of the snub dodecahedron which have the same symmetry as an icosahedron and a dodecahedron, are oriented in the same way on both solids.
The snub dodecahedron, incidentally, comes in both a left-handed and a right-handed form, unlike the solids we have seen here.
If one replaces the dodecahedron by the cube, and the icosahedron (each of these is a dual of the other; the dual of a polyhedron is the one whose corners correspond to the centers of that polyhedron's faces) by the octahedron, one can follow the same steps to get a set of analogous Archimedean solids to those we've seen so far (including the snub cube, also not depicted):
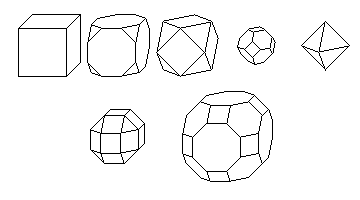
In the first row, we see the cube, followed by the truncated cube, the cuboctahedron, the truncated octahedron, and the octahedron. In the second row, the small rhombicuboctahedron and the great rhombicuboctahedron are presented. Even their names indicate how they correspond to the analogous polyhedra in the dodecahedron to icosahedron series above.
Again, here is the snub cube unfolded:
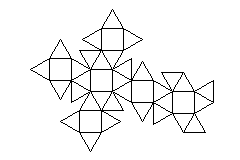
Finally, the tetrahedron may also have its corners truncated, producing the truncated tetrahedron:
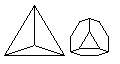
If we were to truncate the corners more deeply, so as to change the existing faces to triangles pointed the other way instead of hexagons, we would not obtain an Archimedean solid, but instead another Platonic solid, the octahedron.
The dual of the icosidodecahedron happens to be an interesting shape, the rhombic triacontahedron, just as the rhombic dodecahedron is the dual of the cuboctahedron. Starting with the rhombic triacontahedron, and connecting the centers of its faces to produce the icosidodecahedron, this is illustrated below:
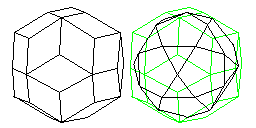
The rhombic triacontahedron is a very interesting shape, because of the explicit way in which it embodies the symmetries shared by the dodecahedron and icosahedron. Thus, both these Platonic solids may be very easily produced from the rhombic triacontahedron, by connecting together each of its two types of vertices, as illustrated below:
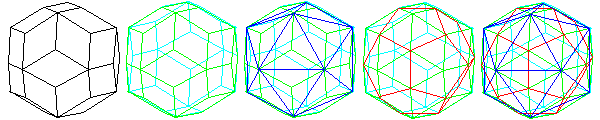
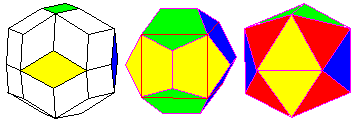
The rhombic triacontahedron also makes obvious a symmetry that the dodecahedron has that is not at all obvious, and quite surprising. There is a relationship between selected edges of the dodecahedron and the cube. This diagram illustrates that relationship, and also shows how the icosahedron also relates to the cube and even the octahedron.
Two subsequent pages will deal with how the small rhombicosidodecahedron might be useful in making a molecular model set, and how there are some additional symmetries present in the Platonic and Archimedian solids based on the coordinate locations of their points.
Tilings may be formed by analogy with the Archimedian solids as well.
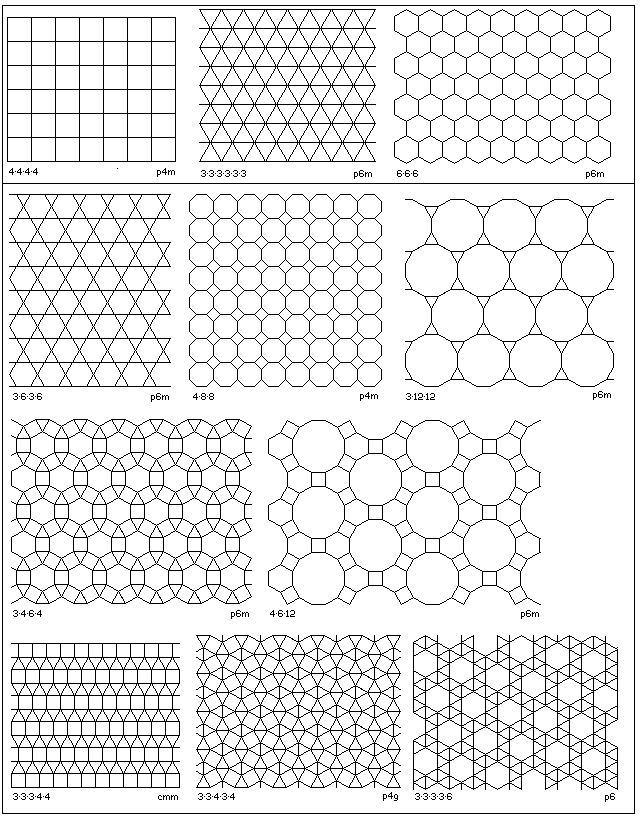
The 11 tilings illustrated above are known as the Archimedian tilings. This is somewhat surprising, as one would have expected the three tilings in the row at the top to be known as the Platonic tilings, and only the eight other tilings to be referred to as the Archimedian tilings.
Oh, and by the way, I found a much better page about Archimedean solids elsewhere on the Web.