Looking at the various Archimedean solids, as well as the Platonic solids, one might note that there are various ways in which one might make other shapes based on them.
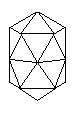
Thus, one could take an icosahedron, and extend it by duplicating the middle portion, to obtain the shape that forms the "head" of one type of bacteriophage:

The number of ways one could make such combinations is, of course, unlimited. If we were to consider a limited set of shapes, by considering only those shapes which are convex, which the solid above is not, and with faces composed of regular polygons (excluding the infinite sets of prisms and antiprisms), we are looking at the Platonic solids (except the cube, which is a prism, and the octahedron, which is an antiprism), the Archimedean solids, and an additional 92 solids, the Johnson solids, named for Norman W. Johnson, who described them in a paper published in 1966. That the list of 92 solids was complete was proved later by Victor Zalgaller.
Not all of these are related to the Platonic and Archimedean solids in a simple way, but many of them are.
For example, if we begin with the icosahedron, we can slice it so as to create a regular pentagon on the plane of slicing to create two Johnson solids:
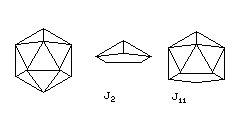
J2, the pentagonal pyramid, and J11, the gyroelongated pentagonal pyramid.
One can do the same thing with the icosidodecahedron and the small rhombicosidodecahedron,
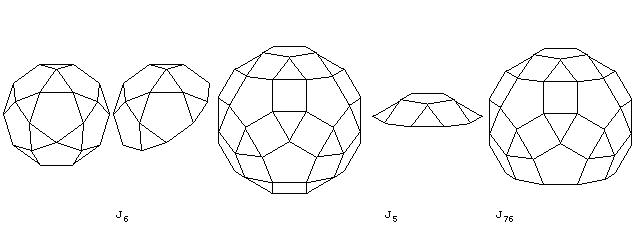
yielding J6, the pentagonal rotunda, J5, the pentagonal cupola, and J76, the diminished rhombicosidodecahedron.
I think I remember J6, the pentagonal rotunda, drawn in a more naturalistic perspective such as that in the image below:
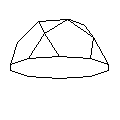
as the shape of an alien spaceship, or a purported alien spaceship, of the "flying saucer" variety in a comic book at one time in my youth. Does this bring back a similar memory to anyone reading this page?
And the same is true of the small rhombicuboctahedron as well,
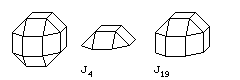
yielding J4, the square cupola, and J19, the elongated square cupola.
And, of course, one must not forget the octahedron,
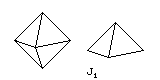
which yields J1, the square pyramid, or the cuboctahedron,
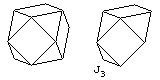
which yields J3, the triangular cupola.
With the small rhombicosidodecahedron, one can also cut more than once:
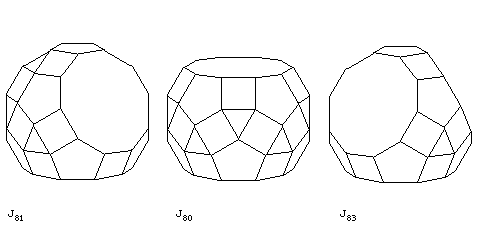
yielding J81, the metabidiminished rhombicosidodecahedron, J80, the parabidiminished rhombicosidodecahedron, and J83, the tridiminished rhombicosidodecahedron.
What can be cut apart can also be put back together, but not quite the way it was before cutting...
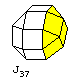
and so one can obtain J37, the elongated square gyrobicupola, as a first example. This shape is also known as Miller's solid, and it is of interest because three squares and one equilateral triangle meet at each of its vertices. Thus, depending on what definition of an Archimedean solid one uses, one might argue that it should be included among that group, although the vertices are not identical in terms of the overall shape of the solid around them.
When it comes to the small rhombicosidodecahedron, the following four solids clearly follow from what we have seen before:
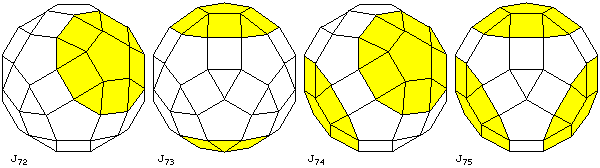
J72, the gyrate rhombicosidodecahedron, J73, the parabigyrate rhombicosidodecahedron, J74, the metabigyrate rhombicosidodecahedron, and J75, the trigyrate rhombicosidodecahedron.
And then there's J34, the pentagonal orthobirotunda:
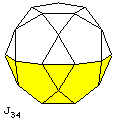
Now, when we put things together, we can also leave some things out. This leads to quite a few additional shapes:

J13, the pentagonal dipyramid, J28, the square orthobicupola, J29, the square gyrobicupola, J31, the pentagonal gyrobicupola, J30, the pentagonal orthobicupola, J32, the pentagonal orthocupolarotunda, and J33, the pentagonal gyrocupolarotunda.
The two component pieces of the pentagonal dipyramid both came from the icosahedron, the two component pieces of the square orthobicupola and the square gyrobicupola both came from the small rhombicuboctahedron, and the two component pieces of the pentagonal orthobicupola and the pentagonal gyrobicupola both came from the small rhombicosidodecahedron. But with the pentagonal orthocupolarotunda and the pentagonal gyrocupolarotunda, one piece from the small rhombicosidodecahedron is combined with one from the icosidodecahedron.
Another two solids one can achieve, by combining parts of different Platonic solids with abandon, are the elongated square pyramid, and the elongated square dipyramid, by placing one or two square pyramids on a cube. While the infinite families of prisms and antiprisms (with squares and equilateral triangles making up the round belt between the two regular polygons of arbitrary type) are excluded from the set of Johnson solids, these shapes can still be added to other shapes to make new Johnson solids. We have already met some examples, where a prism added to a square cupola yields the elongated square cupola, or an antiprism added to a pentagonal pyramid yields the gyroelongated pentagonal pyramid. This produces quite a few of the Johnson solids. Some of those so produced are shown in the diagram below:
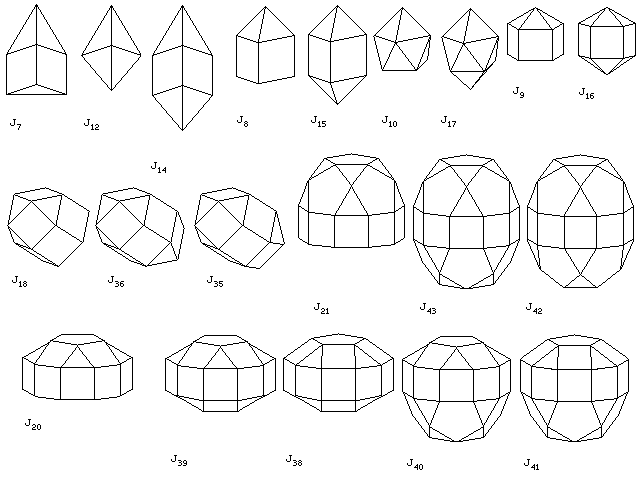
In the first row, we see J7, the elongated triangular pyramid, J12, the triangular dipyramid, and J14, the elongated triangular dipyramid; J8, the elongated square pyramid, J15, the elongated square dipyramid (a plain square dipyramid is, of course, an octahedron, and hence does not belong here), J10, the gyroelongated square pyramid, and J17, the gyroelongated square dipyramid; J9, the elongated pentagonal pyramid, and J16, the elongated pentagonal dipyramid. We previously encountered the gyroelongated pentagonal pyramid, and a gyroelongated pentagonal dipyramid is, of course, an icosahedron, and also is not found here. In the second row, we see J18, the elongated triangular cupola, J36, the elongated triangular gyrobicupola, and J35, the elongated triangular orthobicupola; J21, the elongated pentagonal rotunda, J43, the elongated pentagonal gyrobirotunda and J42, the elongated pentagonal orthobirotunda. In the third row, we see J20, the elongated pentagonal cupola, J39, the elongated pentagonal gyrobicupola, J38, the elongated pentagonal orthobicupola, J40, the elongated pentagonal orthocupolarotunda, and J41, the elongated pentagonal gyrocupolarotunda.
So far, we have only covered 45 of the 92 Johnson solids. A few more shapes are reasonably simple to draw, without having to add too much to pieces derived from the existing drawings of the Archimedean solids:
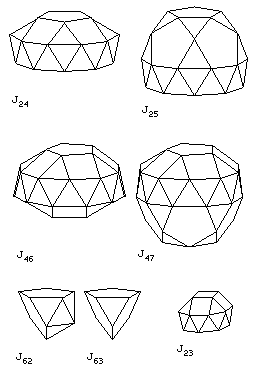
J24, the gyroelongated pentagonal cupola and J25, the gyroelongated pentagonal rotunda. Also not too difficult are J46, the gyroelongated pentagonal bicupola, and J47, the gyroelongated pentagonal cupolarotunda; note that these two shapes have distinct mirror reflections. As well, it is also relatively easy to draw J62, the metabidiminished icosahedron and J63, the tridiminished icosahedron. (A diminished icosahedron would be the gyroelongated pentagonal pyramid, which we have already met, and a parabidiminished icosahedron would be an antiprism, specifically excluded.) Also, J23, the gyroelongated square cupola is included in this diagram.
And here are four more:
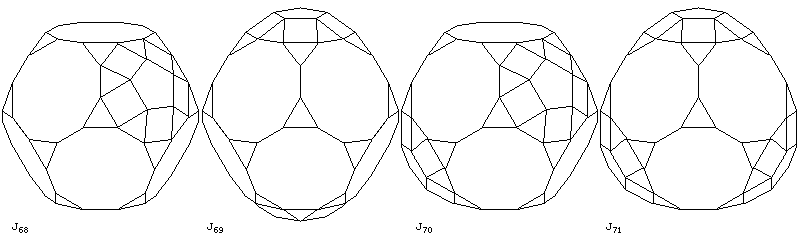
J68, the augmented truncated dodecahedron, J69, the parabiaugmented truncated dodecahedron, J70, the metabiaugmented truncated dodecahedron, and J71, the triaugmented truncated dodecahedron.
It is also reasonably possible to draw the following shapes by the methods I have been using:
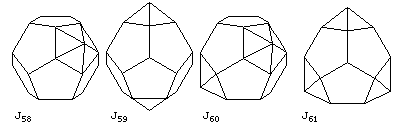
Here are J58, the augmented dodecahedron, J59, the parabiaugmented dodecahedron, J60, the metabiaugmented dodecahedron, and J61, the triaugmented dodecahedron.
And here are some more shapes that can be drawn with relative ease:
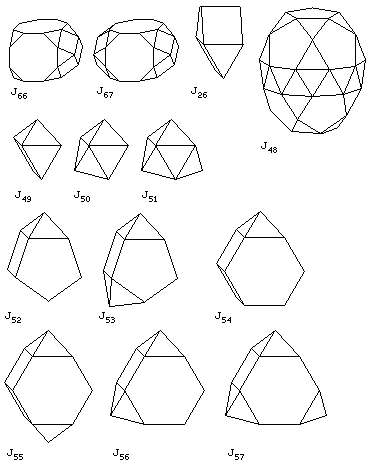
J66, the augmented truncated cube, and J67, the biaugmented truncated cube (these shapes are convex, though the diagram might cause one to wonder); J26, the gyrobifastigum, made from two triangular prisms joined at right angles at one of their square edge faces; J48, the gyroelongated pentagonal birotunda (this one required a particular effort to draw by hand); J49, the augmented triangular prism, J50, the biaugmented triangular prism, and J51, the triaugmented triangular prism; J52, the augmented pentagonal prism, and J53, the biaugmented pentagonal prism; J54, the augmented hexagonal prism, J55, the parabiaugmented hexagonal prism, J56, the metabiaugmented hexagonal prism, and J57, the triaugmented hexagonal prism.
We have already seen the augmented cube, as the elongated square pyramid, and the parabiaugmented cube, as the elongated square bipyramid.
There are still a few more shapes that can be drawn with reasonable ease that have not yet been examined:
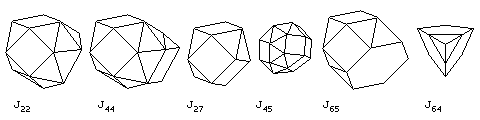
J22, the gyroelongated triangular cupola, J44, the gyroelongated triangular bicupola, J27, the triangular orthobicupola, J45, the gyroelongated square bicupola, J65. the augmented truncated tetrahedron, and J64, the augmented tridiminished icosahedron.
As well, the shapes derived from the small rhombicosidodecahedron that combine both removing some pentagonal cupolas and rotating other pentagonal cupolas have been omitted from consideration so far:
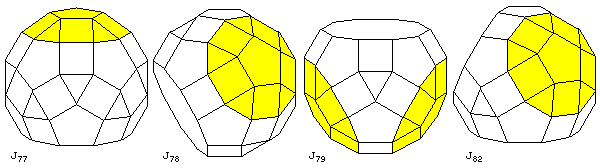
here, we see J77, the paragyrate diminished rhombicosidodecahedron, J78, the metagyrate diminished rhombicosidodecahedron, J79, the bigyrate diminished rhombicosidodecahedron, and J82, the gyrate bidiminished rhombicosidodecahedron.
Finally, among the shapes that can be drawn with reasonable ease, a surprising shape can be derived from some of the faces of the icosidodecahedron. If one joins two pieces consisting of two pentagons and two triangles, the space between them happens to be just right for one square and two triangles on each side.
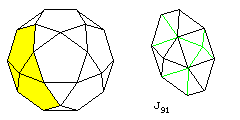
This solid is J91, the bilunabirotunda.
A search, of course, will enable one to find sites that deal with the entire complement of Johnson solids, rather than simply the 84 out of 92 which are shown here. The ones omitted tend, in most cases, to be more difficult to draw than the ones shown here, which, being closely related to the Archimedean solids, or other simple shapes, could be drawn by using parts from diagrams created before, with relatively simple additions. This page, however, I think has the virtue that it gradually introduces the different solids discussed, step by step, and thus it is easier to understand exactly what shape each of the solids discussed has.
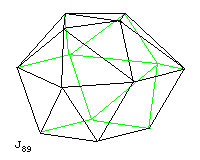
There are eight particularly difficult shapes to draw that have been avoided so far. These are J84, the snub disphenoid, J85, the snub square antiprism, J86, the sphenocorona, J87, the augmented sphenocorona, J88, the sphenomegacorona, J89, the hebesphenomegacorona, J90, the disphenocingulum, and J92, the triangular hebesphenorotunda. I account these as hard to draw, as they involve edges at particularly odd angles.
At least four of these eight shapes, however, have some symmetries which do allow images of them to be drawn by hand, and which allow their structure to be made comprehensible:
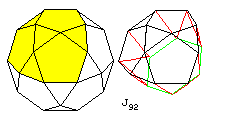
J92, the triangular hebesphenorotunda, also has a relationship to the icosidodecahedron. One can begin with an area from that solid consisting of three pentagons and four triangles, one in the center. From the three outside triangles, one can suspend three squares, and join them to alternate sides of a hexagon. The three gaps, consisting of two sides from a pentagon, one side from each of two squares, and one side of the hexagon, can each be filled by three triangles to form this solid.
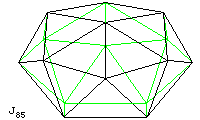
J85, the snub square antiprism, is a highly symmetrical shape. In the diagram, a square is shown as the face on the top, and another square is the base of the solid, directly below it and rotated 45 degrees. Groups of three triangles adjoin each side of each square; they are are so tilted that the solid has an octagonal shape when viewed from the top, the edge of the octagon being a zig-zag band around the middle of the solid.
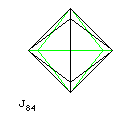
J84, the snub disphenoid, has a similar symmetry. This time, it is viewed from the top in this diagram, with green lines showing hidden edges. It begins with two bent lozenges composed of two equilateral triangles, on top and bottom at right angles. A pair of triangles joins each side of the top lozenge to its corresponding side on the bottom lozenge.
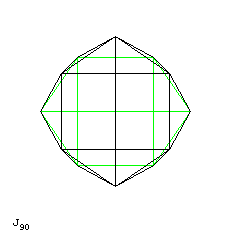
J90, the disphenocingulum, also has this form of symmetry. Here, we again view the solid from what we will consider to be the top. On the top and bottom we have two squares, folded symmetrically at an angle like the roof of a house, each being at a 90 degree angle to the other. A cluster of five equilateral triangles joins two sides adjacent to the line joining the two squares on one of the sets of two squares to a side away from and parallel to the line joining the two squares on the other set of two squares in each of four cases.
Finally, for three of the four that I find to difficult to draw, here are drawings of their surfaces in an unfolded state. Colors have been used on their edges to indicate which edges are to be joined to each other.
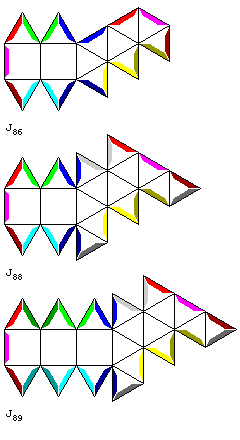
Depicted here are J86, the sphenocorona, J88, the sphenomegacorona, and J89, the hebesphenomegacorona.
It can be seen that all these shapes are closely related. Either the middle one of three square faces, or the edge between the two square faces, can be thought of as being on the bottom, and the edge between two triangles would be on the top. One way, perhaps, of getting a clear concept of the orientation of each face in these shapes would be to take the most complex of them, and think of it as being the shape of a futuristic automobile.
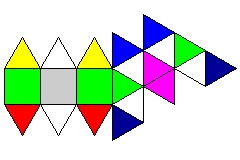
Let the gray square face be the bottom of the car, where the four wheels are. The two blue faces would be the front window, the two dark blue faces the rear window. The yellow faces are where the headlights would be located, the red faces where the taillights would be located. The green faces indicate the doors on both sides of the car. The purple faces form the bent lozenge that is the roof of the car.
Here is an attempt on my part to crudely sketch this shape, but the proportions and apparent angles in this drawing may be misleading:
I did make an effort to make parallel edges parallel, which is what gives this sketch an air of plausibility. Also, by showing the hidden lines, and previously explaining the symmetry of the shape through the use of its unfolded surface, at least some understanding of the shape is possible when the diagram is seen.
J87, the augmented sphenocorona, is formed from J86, the sphenocorona, by placing a square pyramid on one of its square faces.
It may be noted that, just as the relationships between the Platonic and Archimedian solids explored on the preceding page can be studied and experienced with the Zome System, another type of educational toy, two versions of which are made by different companies as Jovo (Denmark) and Polydron (United Kingdom) lends itself to the construction of these solids. This category of educational toy is not as profoundly mathematical as Zome, but consists of pieces in the shape of regular polygons, all with edges of the same size, which have edges that join androgynously to create hinges.