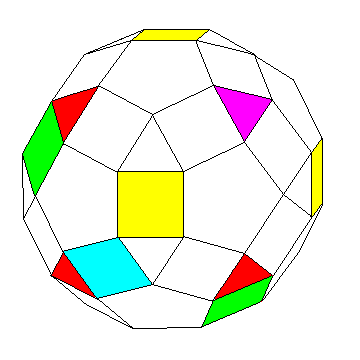
This illustration of the small rhombicosidodecahedron shows how the fact that a selected group of faces of the icosahedron has faces with orientations matching those of the octahedron, along with the fact that a set of faces of the rhombic triacontahedron has orientations matching those of the faces of the cube, may be useful:

The yellow square faces follow the symmetry of the six faces of a cube. (All the square faces have the symmetry of the thirty faces of the rhombic triacontahedron, or the thirty edges of the icosahedron, or the thirty edges of the dodecahedron.)
By symmetry, therefore, the four colored triangles (three colored red, one colored purple) correspond to the faces of the octahedron in symmetry. At least in terms of where they are centered, and the direction in which they face; they are rotated compared to the faces of the corresponding octahedron.
The square faces colored in two shades of green in this diagram are positioned halfway between the purple triangle and the one opposite it, and their centers are spaced at 120 degree angles from the center of the solid.
The following diagram may make the symmetry that leads to this clearer:
Why is this useful?
The carbon atom in methane is bound to four hydrogen atoms in a symmetrical fashion, corresponding to the symmetry of a tetrahedron.
The angle between tetrahedral bonds happens also to approximate the angle between chemical bonds in water and ammonia as well.
Thus, a great many molecules can be represented using models in which the spheres representing atoms have holes drilled in them at angles corresponding to the faces (or corners) of the tetrahedron.
The bonds from some other atoms can be represented by the six directions corresponding to the faces of a cube.
Both of these directions can be represented by the centers of the faces of a cuboctahedron, and one popular brand of molecular models, invented by Kazuhisa Sato, uses cuboctahedra instead of spheres to represent atoms.
But another symmetry sometimes found in the bonds from an atom is known as the trigonal bipyramid, in which three bonds radiate out from the atom at 120 degree angles, and two others are perpendicular to the trianglular portion.
Thus, this Archimedian solid permits this symmetry also to be represented without having to resort to shapes derived from the triangular prism.
It may be noted that, in addition to spheres representing hydrogen atoms, and the shape used for the trigonal bipyramid bond arrangement, which is a bisected cuboctahedron with a layer of twelve rectangles inserted, some sets in this series also include atoms in the shape of the great rhombicuboctahedron and the icosidodecahedron.
Except for using rectangles having the Golden Section ratio instead of squares, so that the triangles can be larger relative to the pentagons, and using connecting rods of triangular, pentagonal, or rectangular cross-section, (which, incidentally, are yellow, red, and blue in color respectively, and which, in the case of the triangular and pentagonal ones, are not prisms, but invert the orientation of the shape from one end to the opposite, so that all the modified small rhombicosidodecahedra have the same orientation), the same idea has already been thought of, and is the basis of a model set used for geometrical education as well as an educational toy.
This model set has recently been expanded to include green connecting rods, which, like the pieces in the shape of the great rhombicuboctahedron in the molecular model set mentioned before, allow connections between points to be made in an important set of directions not perpendicular to any of the faces of the small rhombicosidodecahedron. To address this, what I would envisage in the type of molecular model set that I am outlining here is using elements in the shape of the small rhombicuboctahedron (but again with rounded corners, as noted below) but with faces larger in size so that they would be roughly the same size as those in the shape of the small rhombicosidodecahedron.
In addition to being cubes, sometimes dice are made with such rounded corners that they are spheres with circular flat faces oriented in the same direction as the faces of a cube. It is possible to make dodecahedral or even icosahedral dice this way, and, in my opinion, a similar shape based on the small rhombicosidodecahedron would be a particularly attractive shape to represent atoms in molecular models: the fact that there would be, among the faces, flat faces oriented like those of a cube, would provide ease in storage; the generally round shape would be less distracting than a polygonal shape, and would provide a basically spherical appearance, as is conventional for atoms in molecular models; but the presence of distinct and identifiable faces would still make it easier to place bonds in the intended part of the atom-representing element.
The shape I envisage would look something like this:

My conception of how this might be used is:
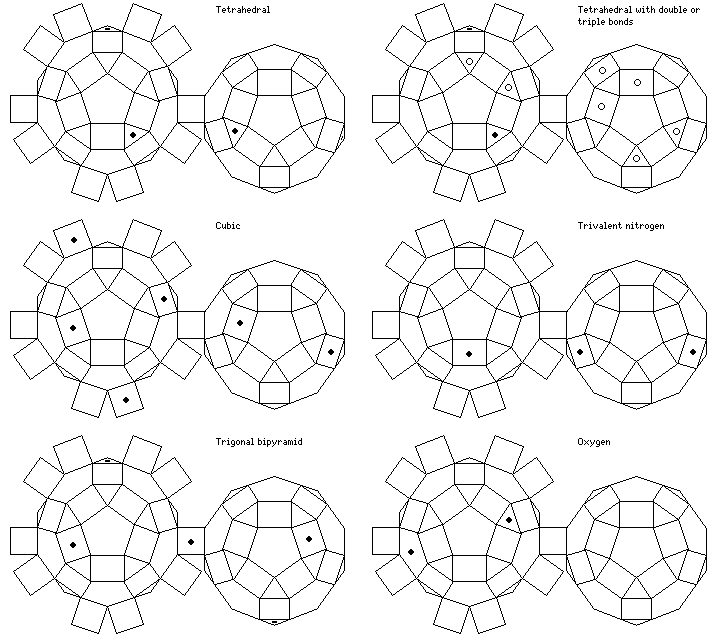
The three holes shown for trivalent nitrogen are separated from each other by 108 degrees each; this is a closer approach to 107 degrees than the 109.4712 degrees provided by a tetrahedral arrangement.
As for the oxygen bond, the 104.5 degree angle required is most closely approached by the 101.8123 degree angle between a pentagonal facet and a triangular facet shown in the diagram.
Except for this, though, the pentagonal faces are almost never used. Thus, for most types of atom, the circular caps corresponding to these faces need not be trimmed off, leaving the atom mostly spherical. The hydrogen atom would be represented by a small sphere, and, as noted above, some types of atom would instead have a shape based on the small rhombicuboctahedron.
This image (produced, of course, by ray-tracing) illustrates one way in which a molecular model set could provide different types of atom:

The different kinds of atom depicted in the diagram are in the arrangement:
nitrogen hydrogen sulfur carbon metal oxygen phosphorus silicon chlorine
Nitrogen, carbon, phosphorus and silicon are all shown with the most common arrangement of faces, where the flat circular areas correspond to the square and triangular facets of the small rhombicosidodecahedron only. This allows bonds from these elements to be arranged following the patterns of the tetrahedron, the trigonal bipyramid, the cube, and other arrangements, including allowing flexibility in using double bonds (envisaged as generally involving two triangular faces separated only by a square face).
The buff-colored metal atom has flat circular areas corresponding to the twenty-six faces of the small rhombicuboctahedron instead, allowing both the face-centered cubic and body-centered cubic lattices to be formed with this type of ball.
Hydrogen is simply a small sphere, since normally only one bond leads to a hydrogen atom: putting a hole right through it, like a bead, allows ionic molecules to be depicted.
Sulfur and oxygen would have most of their needs met by flat circular areas corresponding to the triangular and pentagonal faces, as this permits the construction of a double bond, and it allows the angle between a triangular area and a pentagonal are to be used; but since bivalent oxidizing elements may also be found in the rock salt lattice with bivalent metals, circular areas corresponding to the square faces of the small rhombicosidodecahedron as well.
Chlorine is shown with flat circular areas corresponding to the square and pentagonal facets of the small rhombicosidodecahedron only. While in most cases, only a single bond comes from a chlorine atom, allowing the use of a simple sphere like that shown for hydrogen, the other possibilities are covered by the available faces: the square faces allow the representation of the lattice structure of sodium chloride, a plain regular cubic array of alternating atoms, and together the square and pentagonal faces allow the pentagonal bipyramid to be depicted, covering the reversed valence case. (Actually, the pentagonal faces would only be needed for iodine, since fluorine and chlorine are too strongly halogenic to be reversible; their use is in allowing the construction of a model of iodine heptafluoride.)
The image above shows all the spheres except the plain sphere representing hydrogen as equal in radius. In practice, the radii might be proportional to the Van der Waals radius of each kind of atom, perhaps from 40% to 25% of that radius on the scale on which bonds are represented. However, I envisage rounding off these radii, to, for example, 1.2, 1.5, or 2 times the radius used for the carbon atom, so that the spheres, packed as cubes with the aid of the flat faces corresponding to the square faces of the small rhombicosidodecahedron, would fit neatly into a box with no wasted space.
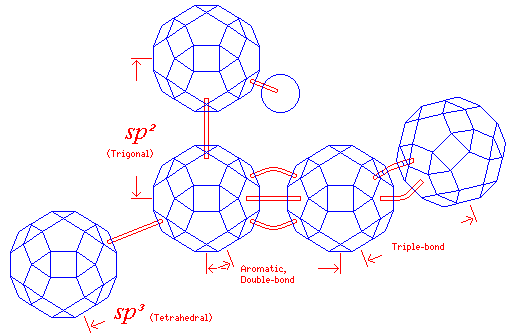
This diagram shows how I envisage the length of bonds can be represented with this type of model.
Incidentally, the names given for bonds in the tetrahedral and trigonal bipyramidal arrangements derive from quantum mechanics. One set of linearly independent solutions to Schrödinger's equation in spherical co-ordinates for an electron orbiting a nucleus provides one s orbital, where the probability distribution of the electron is a sphere centered on the nucleus, and three p orbitals, which look like the solid of rotation generated by a figure-8 pattern, oriented with their major axes along the x, y, and z axes respectively.
The state of a quantum system depends on the observation being made upon it; if one observes the position of a free particle, its wave function is forced into a position eigenstate (in which its location is known, but its velocity can be anything); if one observes the momentum of a free particle, its wave function is forced into a momentum eigenstate (in which it is moving at a definite velocity, but it can be anywhere).
When an atom is part of its molecule, its interactions with its neighbors constitute an observation, changing the basis set of states in which its valence electrons are found. If the bonds are in tetrahedral directions, the s state and the three p states are replaced by a set of four spatially symmetric states pointing in the directions of the four vertices of the tetrahedron; this is called sp3 hybridization.
When the bonding is of the trigonal bipyramidal kind, one p state is left alone, and the s state and the other two p states are replaced by three spatially symmetric states pointing in the directions of the corners of a triangle; this is called sp2 hybridization.
The holes in the faces corresponding to triangles would be relatively shallow, because the bonds which proceed from an atom in tetrahedral directions are greater in length; the square holes would have deeper holes, so that the same connecting rod would give the shorter length of a bond where the symmetry is triangular.
There are two cases for triangular symmetry, and in the aromatic case, the bond is even shorter. This would require a shorter connecting rod; also, because of the large disparity in size between both the bond to a hydrogen atom, and the sphere representing one, a shorter connecting rod would be needed for that.
Double bonds would be indicated by a pair of curved pieces in the two triangular faces adjacent to a square face. In the diagram, the aromatic bond length and the double bond length are assumed to be the same, with aromatic rings indicated by alternating single and double bonds; this does not necessarily have to be the case, and instead the connecting rods used for each type of bond could be designed to represent the two different lengths of the two different kinds of bonds accurately, at least for one element (presumably carbon). In that case, the central portion of the shorter rod for an aromatic bond should be made thicker, to indicate it represents a bond and a half.
A triple bond is indicated by three curved pieces in the three square faces adjacent to a triangular face; since the holes in the square faces are deeper, the triple bond would be shorter. As long as the same curved piece is used, since no additional degree of freedom is introduced, the triple bond would not have the exactly correct scale length.
It is even possible, using this shape as the basis, to create a model of the Fullerene with sixty carbon atoms, using a configuration of holes as shown:
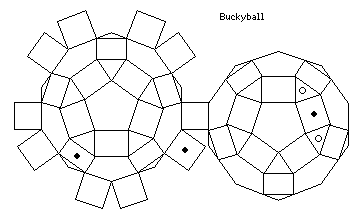
and we will see why this is possible in the next section.
The circles in the diagram of the configuration of holes would allow those bonds which serve as the border of two hexagons in the image above to be replaced by double bonds.