
Below is a photograph of a specimen of that most mysterious artifact of antiquity, the slide rule.

And here is the diagram by which I formerly attempted to illustrate the appearance of one:
How could such a strange-looking object be used to perform calculations?
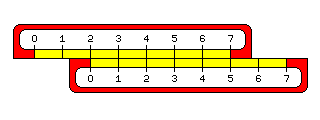
The underlying principle of the slide rule is simple enough. If you take two ordinary rulers, and starting from a position of two units - two inches, two centimeters, whatever you care to imagine - measure a further three units with another ruler, you will obtain a distance of five units - which the first ruler will indicate.
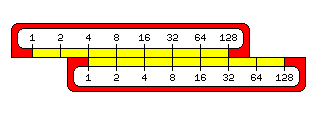
Multiplication behaves like addition. If you multiply 2 by itself over and over, you will get the powers of two, and 8 times 32 is the same as 16 times 16, just as 3 plus 5 is the same as 4 plus 4.
If, instead, you multiplied a number that was very close to 1 by itself, you could find at least an approximate place to put every number in order to multiply by adding. This place, this value which corresponds to numbers, so that when added, it yields the value corresponding to their product, is called a logarithm.
When John Napier first invented logarithms, that was the technique he used to begin calculating the very first table of logarithms.He made three very short tables, each one based on a different number that had a very small difference between itself and 1: 9,999,999/10,000,000, 99,999/100,000, and 1,998/2,000. By looking 99,999/100,000 up in the first table, he was able to work out a correction factor for combining the two tables, and then he used the first two tables to determine where 1,998/2,000 would fit in.
We now know easier ways to calculate logarithms. One series formula for the natural logarithm of a number is:
2 3 4 5 6
u u u u u
ln(x) = u + --- + --- + --- + --- + --- +...
2 3 4 5 6
where
x-1
u = -----
x
Since the logarithm of x goes to minus infinity as x goes to zero, a simple series in x itself isn't feasible.
The logarithm function is the inverse of the power function. Thus, 4 is 2 to the second power, 8 is 2 to the third power, 16 is 2 to the fourth power, and 2 is the logarithm of 4 to the base 2, 3 is the logarithm of 8 to the base 2, and 4 is the logarithm of 16 to the base 2.
Common logarithms are logarithms to the base 10. This makes them convenient for doing arithmetic, because the integer part of a common logarithm indicates where to put the decimal point, and the fractional part is the same for the logarithm of 326, 32.6, or 3.26, so that tables need only contain the fractional part of a common logarithm.
Natural logarithms are logarithms to the base e, where e is 2.71828..., a fundamental constant like pi. These logarithms are more fundamental when working with calculus, but aren't as useful for everyday calculations. But while common logarithms are the basis of the slide rule, natural logarithms will turn up when we examine more advanced scales.
Here we see two slide rule scales set up to multiply the numbers on the bottom scale by 2. Thus, 1 was placed under the 2; therefore, 2 is under the 4, 3 is under the 6, 4 is under the 8, and 5 is under the 10.
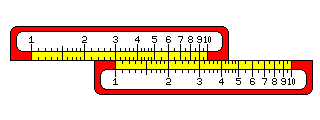
This works just as well for other numbers; here, the 1 is placed under the 3, and so the 2 is under the 6, and the 3 is under the 9.
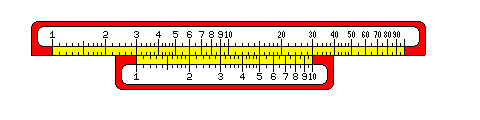
But what happens to the other numbers when they're multiplied by 3? One way to find out would be to add a second scale to the end of the top scale. This way, we see the following:
The small tick marks between "10" and "20" divide the area between them into ten parts, so each small tick mark in that area stands for 1. Thus, we can see that the 4 stands under 10 and two tick marks, or 12.
Similarly, 5 stands under 15, and 6 stands under 18.
From 20 to 50, there are only five tick marks between each number and the number that is 10 greater. So each tick mark stands for 2.
Thus, we see that 3 times 7 is 21, since the 7 is under a point about halfway between the 20 and the first tick mark following it.
On the other hand, that 3 times 8 is 24 is easy to see, as that falls under the second tick mark after 20.
And, since 3 times 9 is 27, again we see that the 9 is between the tick marks that represent 26 and 28.
Finally, the 10 falls under the 30.
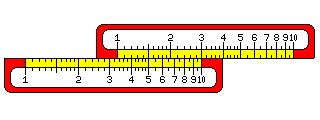
Noting how the scales on a slide rule simply repeat themselves, one can put the 10 instead of the 1 under the number by which one wishes to multiply to see the other possible products. This lets one use the C and D scales, instead of the A and B scales, which are on a smaller scale, to multiply, giving more accuracy.
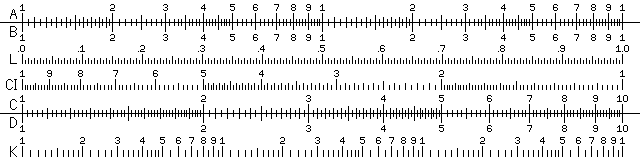
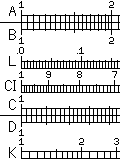
Having seen how to do basic multiplication on a slide rule, we can now understand the basic scales on a slide rule, as shown in the first image above.
One difficulty some beginners have with the slide rule is simply finding numbers on its scales.
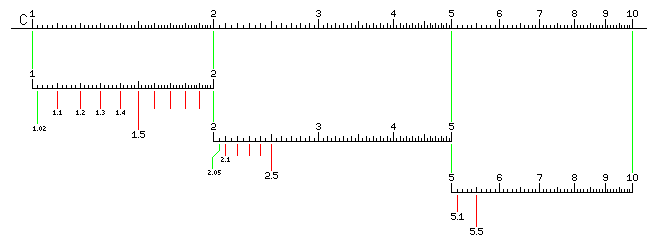
This is not terribly complicated in itself; between the numbers on a slide rule, there are tick marks large and small, laid out in much the same way as they would be on a ruler or on the tuning scale of a radio. However, because slide rules multiply instead of adding, their scales aren't uniform like that of a ruler. To make it possible to read numbers with precision, the tick marks are kept close together, and so along the length of the rule, their scheme changes.
Thus, in the illustration above, the space between the numbers 1 and 2 is first divided into halves by one large tick mark, then into tenths by several medium tick marks, and the tenths are themselves divided into five parts by small tick marks.
So on this part of the slide rule, the space between two adjacent tick marks represents one-fiftieth of that between two numbers on the scale.
Between the numbers 2 and 5, the space between two consecutive digits is first divided into halves by a large tick mark, then into tenths by medium tick marks, and each tenth is divided in half by a small tick mark. So here, the space between two adjacent tick marks is one-twentieth of that between two numbers on the scale.
And between 5 and 9, the scale looks like the centimeter scale on a typical ruler; the space between two numbers is divided into halves by a large tick mark, and then each half is divided into five parts by a small tick mark. Here, the space between two adjacent tick marks is one-tenth of that between two numbers on the scale.
This is how the C scale would be marked on a typical 5-inch slide rule. On a 10-inch slide rule, space for twice as many tick marks would be available, and so the layout would be different. Thus, the difficulty really is that it's necessary to pay attention to how the tick marks are laid out on the part of the slide rule on which one wishes to find a number at any given time.
If you multiply a number by itself, the result will be twice the distance from the index - the 1 mark - as the original number was. So if you have two slide rule scales, one twice as big as the other, if their indexes are aligned, each number on the scale that is twice as big corresponds to the location of its square on the smaller scale.
Thus, the A and B scales, at half the side, with the scales repeated twice, aren't just for beginning slide rule users. Rather, they let people work with squares and square roots.
Similarly, the K scale is at one third of the scale of the C and D scales, and so it is used for cubes and cube roots.
The CI scale is the same as the C scale, except it runs backwards. Since division is the opposite of multiplication, this scale can be used to find reciprocals.
Of course, it's obvious from the way that multiplication is performed on a slide rule that you can perform division without the need for such a scale; going from 3 to 1 measures out the same distance backwards as going from 1 to 3 does forwards. So if you place the 1 on one scale under the 3 on the other, not only can you see 3 times any number on the bottom scale on the top scale, but you can also see any number on the top scale divided by 3 on the bottom scale.
The L scale is a uniform linear scale, and is used to read off the fractional portion (or mantissa) of the common logarithm of numbers on the C scale.
Note that the illustration of a simple slide rule at the top of the page corresponds to the distribution of tick marks on a 5-inch slide rule (actually, one with a 12.5 cm scale), not the usual 10-inch (25 cm) slide rule. Despite this, and despite the use of 600 pixels to represent the scale width, the positions of the tick marks are noticeably uneven. Because slide rules have scales which gradually vary in size, they are very difficult to depict well in discrete pixels.
A BASIC program was used to draw a picture in the .xbm file format, containing the plain scales with ticks of varying size and spacing but no numerals, which I then viewed with a web browser, and got into a paint program by using the clipboard.
A width of 600 pixels was chosen to allow the L scale, at least, to appear uniform, and to allow the two repeated occurences of the scale on the A and B scales, and the three occurences on the K scale, to be identical.
For the other diagrams on this page, one copy of the scale from the K scale was used to represent the C and D scales, and a slightly smaller scale was used, so that the distance between 1 and 2 was exactly 53 pixels, and the distance between 1 and 10 was 176 pixels. (The same program drew the log-log scale used in the diagrams above; instead of replying 600 to the prompt for the width of the slide rule, I replied 528, which is three times 176, to obtain the raw materials for those diagrams.) As noted on my page about the musical scale, this particular division allowed ratios involving 2, 3, and 5 to be well-represented. Thus, while the irregularity in the spacing of the ticks could not be eliminated, at least it repeated at convenient intervals so that the rules could be shown sliding against each other in diagrams which gave a reasonable appearance without having to cheat by shifting some of the ticks by hand from their calculated positions. (I had tried other possibilities, involving approximations only to log(2), but because that is 0.3010299... rational approximations to it, while good, are widely spaced, or involving computer searches for ratios that minimize error over all the tick marks, but they were not as successful.)
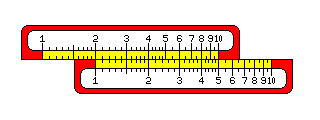
Incidentally, some older slide rules have an appearance like this:
Although this makes them more difficult to read, by isolating the eye from the varying heights of the ticks, this arrangement may have been presumed to have the effect of reducing bias in estimating positions between tick marks.
The modern type of slide rule scale started to appear around the year 1910, but some European slide rule makers, notably Unique in Britain and Nestler in Germany, retained the old style of scale for decades thereafter.
My explanatory diagrams above don't quite use this arrangement; instead, I was trying to dramatize the difference between tick marks further to make the diagrams easier to follow; thus, only major tick marks close a box in what I have drawn, quite the opposite of the older slide rule design.
The slide rule, once widely used by people working in engineering and the sciences, was swiftly displaced by pocket calculators when they became available. An inevitable question, then, is: when did the slide rule "die"?
Long after the slide rule was displaced, though, there were still metric conversion gadgets which operated on the same principle as a slide rule, with logarithmic scales, so one can claim that to some limited extent it still lives on.
Here are three dates which are important milestones in the process:
February 1, 1972 HP 35 scientific calculator $395 January 15, 1974 TI SR-50 scientific calculator $170 June 13, 1976 TI-30 scientific calculator $24.95
Since a good quality slide rule cost about $25 at the time, at least one web site has proclaimed June 13, 1976 to be the day on which the slide rule "died".
I think these three dates are helpful, but some additional information is needed to provide a context.
Before Texas Instruments came out with the SR-50, Bowmar was charging a similar price for a scientific calculator they made. Unlike the TI calculator, though, it was more limited in some respects; one major limitation of the Bowmar MX-100 Scientific Brain was that it had no Enter Exponent key, and could not display results in scientific notation. This was built around a chip designed for building single-chip calculators from Rockwell.
So after the SR-50 came out, some of those calculators may have been sold off at reduced prices.
My first scientific calculator was a Microlith Scientific, Model 205. It had exponent entry, unlike the Bowmar, but it was limited in that it only had eight digits of precision, and log and trig functions were only calculated to five digits of precision. This was also a single-chip calculator; it was not based on one of the single-chip scientific calculator chips from MOS Technology, as their scientific calculator chips, while available in three different configurations, didn't include one for a 25-key calculator. It could have been based on a Rockwell chip, as, while the positions of the keys were different, the shifted functions assigned to each key were identical to those of the Rockwell 63R scientific calculator. The chip that calculator used was the A4802CB.
This was before the TI-30 came out. The Microlith Scientific was introduced in 1974, but its original price was higher.
So if a price point of around $30 or so is what would lead to the "death" of the slide rule, that would have happened some time before the TI-30, and one might have to dig quite a bit through old advertisements to narrow down the exact date.
But there is another issue to consider.
A high-quality slide rule may have cost around $25.00 or so. But there were alternatives. Sterling Plastics made a duplex log-log slide rule, out of plastic, and one ad gives a price for it of $2.98 in 1965. What with inflation, the price in 1976 might have been $6.98 instead, but that's still less than $25.
Why didn't the slide rule stay around, then, until pocket calculators got even cheaper?
For one thing, a pocket calculator was much more convenient and precise than a slide rule, so it wasn't a question of choosing between two equal items, depending on which one had the lower price. For another, while $395 was a lot of money back then, and so was $170, while $25 also was more than $25 is today, it was still in the range where nearly all households could afford an item at that price if there was any genuine requirement or desire for it.
So a $7 slide rule really wasn't much competition to a $25 calculator.