The less expensive slide rules of simplex type have tended to be made according to several traditional fixed patterns. But duplex slide rules, on the other hand, seem to come in a wide assortment of types.
However, many duplex slide rules have an arrangement that at least tends towards something like this:
K A/B S ST T1 T2 C/D DI P LL00 LL01 LL02 LL03 DF/CF CIF L CI C/D LL0 LL1 LL2 LL3 LL4
It's obvious why slide rules would only tend towards this type of arrangement rather than actually having that arrangement. On the back, each half of the stationary part of the rule has five scales, while on the front, the halves have two or three scales. And, on the other hand, the slide has five scales on it in the back, and six in the front.
Why is the arrangement shown above a desirable goal?
It offers the scale subset
A/B C/D DI
which is an inside-out equivalent of the classic "Mannheim" arrangement of
A/B CI C/D
that allows many functions of three variables to be worked out with a simple operation on the rule.
The trig scales are on the slider. Why is this useful? After a number is multiplied by the sine of one angle, holding the cursor in position allows the slider to be moved so that the result can then be multiplied by the tangent of another angle, for example.
Not all the scales on a slide rule work like the trig scales. While a number on the log-log scales might be used as the starting point for a computation, the end result is then read on the log-log scales again. The L scale is also used for reading a final result, and thus doesn't gain anything from being on the slide.
Why is the L scale on the slide, then, in the arrangement shown above? Because it is on the back of the rule, since it is used for calculations of a type related to that for which the log-log scales are used, and they clearly consume the available space on the stationary part of the rule.
The P scale is shown on the front of the rule, as its function is related to the trig functions.
By adding a few scales, one could arrive at a more balanced slide rule arrangement based on the starting point shown above, for example:
Sh1 Sh2 Th K A/B S ST T1 T2 C/D DI DFM L P LL00 LL01 LL02 LL03 DF/CF CIF R1 R2 CI C/D LL0 LL1 LL2 LL3 LL4
The DFM scale, in conjunction with the L scale, can permit the series of log-log scales to be extended upwards to arbitrarily large numbers. Having the R1 and R2 scales on the slider permits higher-precision multiplication to be performed, although with several steps.
The problem with a slide rule like this, though, is that it has 32 scales. In practice, such rules tend to be unwieldy.
Traditionally, even the high-end duplex rules available in North America had either come with a 3/5/3 distribution of scales - three on each stationary part of the rule, and five on the slider, a 4/4/4 distribution of scales, or even a 3/4/3 distribution of scales. Dietzgen rules tended to have the first, Hemmi and Ricoh rules the second, and Keuffel and Esser rules the third.
Hemmi and Ricoh rules, however, might start with a 4/4/4 layout, and then squeeze in one extra scale on one side of the slider; Keuffel and Esser rules, on the other hand, tended to sneak in an extra scale on one side of the stator instead, and rigidly respected the limitation of the slider to four scales.
With a limited number of scales, it is harder to achieve an ideal layout.
The Hemmi 260 slide rule is an excellent example of a slide rule with all the conventional scales in a 4/5/4 format:
LL00 LL0 K A|B T S ST C|D DI P L LL01 LL02 LL03 DF|CF CIF CI C|D LL3 LL2 LL1
with the typical fault of putting the LL00 and LL0 scales on the opposite side of the rule. Because it doesn't include the double-length scale for more precise roots found on the Versalog slide rule and several others, it has room for a DI scale and even a P scale.
The original Versalog, also made by Hemmi, had the more conventional 4/4/4 format, and still managed to fit in the conventional scales and the double-length scale:
LL0 LL00 K DF|CF CIF CI C|D R1 R2 L LL01 LL02 LL03|T ST S C|D LL3 LL2 LL1
Since the double-length scale was present, space could be saved by omitting the A and B scales.
The Deci-Lon slide rule, brought out by Keuffel and Esser in 1961, had a 5/5/3 distribution of scales, giving the arrangement:
LL03 LL02 LL01 LL00 A/B T ST S C/D DI K R1 R2 DF/CF CIF L CI C/D LL0 LL1 LL2 LL3
and, since one has to flip the rule over, around its long axis, to go to the other side, the top becomes the bottom, so there is one wide piece, and one narrow piece, on the stationary side of the rule, not two pieces with five scales on one side and three on the other.
Of the slide rules that could be said to have an optimal scale layout, this one was the one which was best known in North America. This particular slide rule is a highly sought-after and valuable collector's item.
There certainly are, however, other slide rules that had scale layouts which avoided most of the compromises that came with the older slide rules with smaller sets of scales.
A few I would single out for special praise, from among those listed on the previous page, are:
The Graphoplex 690a:
LL00 L T2 A/B T1 ST S C/D P DI LL0 LL01 LL02 LL03 DF/CF CIF K CI C/D LL3 LL2 LL1
The log-log scales are split. Note that the L and K scales are interchanged from their usual positions on a conventional rule; while this does put the wrong one on the front and the back, it puts the right one on the stationary part of the rule and on the slider, which is arguably more important.
Placing the T2 scale on the stationary part of the slide rule preserves both the A/B and C/D scale pairs, This is unusual, but it is very useful for some types of trigonometric calculations. This detail makes this particular rule uniquely optimal for its scale set.
The Pickett Microline 140:
LL01 K A/B T ST S C/D DI LL1 LL02 LL03 DF/CF CIF L CI C/D LL2 LL3
is a conventional rule widely available in North America of smaller size. The Koh-I-Noor 10010 Techni-Log slide rule, also by Graphoplex, had a very similar scale set, but with the L and K scales again interchanged.
The Pickett N500 is another similar rule with the same scale set, although it was less conventional in that it followed Pickett's common practice of pairing scales together from the two log-log series.
Aristo made a large number of slide rules that had scale arrangements I admired. One example, in this range of sizes, is the Aristo MultiLog 0970:
LL00 K A/B T ST S C/D DI LL0 LL01 LL02 LL03 DF/CF CIF L CI C/D LL3 LL2 LL1
Since the stators are both one scale smaller on the front, it is something of a surprise that this rule didn't at least add a P scale, very common on Aristo rules, but that can be explained by the fact that the closely related log-log scales were close together.
A very impressive slide rule from Aristo is their HyperLog 0972:
H2 Sh2 Th K A/B T ST S P C/D DI Ch Sh1 H1 LL00 LL01 LL02 LL03 DF/CF CIF L CI C/D LL3 LL2 LL1 LL0
Although it seems odd for the rule to lack a T2 scale when it has several uncommon scales, as those uncommon scales are in two complete sets (P, H1, H2 and Sh1 Sh2 Th Ch) this is a very well-designed rule. The reverse of the slide, having five scales where the front has six, is spaced apart a bit more generously, but moving the P scale to the rear to make room for a T1/T2 pair is not an option, since it is used with the trig scales.
Note how the Aristo and Graphoplex slide rules place the most-used LL3 portion of the log-log scales closest to the slider.
In comparison to these slide rules, many North American and Japanese slide rules gave up either the A/B scale pair, or the C/D scale pair, on the front of the rule in order to fit in the trig scales on the slider. On the other hand, a number of European duplex rules placed the trig scales on the stationary part of the rule; for example, both the Nestler 0292 and the Faber-Castell 2/83N do this: but the Faber-Castell 2/83N, admittedly, had the good excuse of having to fit quite a bit on the slider to allow a paired set of double-length scales on one side of the rule.
A slide rule with 26 scales, the maximum that might be considered to fit on a conventional slide rule, can present a particularly difficult problem for someone seeking an optimal layout, depending on which scales it is chosen to include. The Deci-Lon and the Graphoplex 690a, as shown above, are two rules that I think were successful in this size range.
If I want to include the same scales as the Deci-Lon, but I also want to place the two R scales on the slider, a first attempt at an optimal arrangment might be:
LL00 LL01 K A/B S ST T C/D DI LL02 LL03 LL0 LL1 DF DIF/CF R1 R2 L C/DI D LL2 LL3
Since the 'Règle des Ecoles' arrangement on the back of the slide rule is intended for multiplication using an inverse scale, in this arrangement I take the unconventional step of placing the inverse scale in contact with the regular scale. In order to place the R scales on the slider, I turn the center of the rule inside-out. This puts a DI scale on the back of the rule instead of a CI scale, and the front already has a DI scale, because of the need to place the trig scales on the slider, but that is only a minor disappointment.
But it is possible to be even a little bolder, to obtain a CI scale and a DI scale on the rule instead of two DI scales, as follows:
LL00 LL01 K A/B R1 R2 CI C/D L LL02 LL03 LL0 LL1 DF DIF/CF S ST T C/DI D LL2 LL3
Moving the trig scales to the back of the rule, where the optimal multiplication scales are, and the R1 and R2 scales to the side of the rule with the A/B and K scales is logical, if unconventional. But the usefulness of this arrangement depends strongly on the scale set used; omitting the R1 and R2 scales to obtain a T1 and T2 scale set and a P scale, for example, leads to the more conventional Graphoplex 690a arrangement, or something like it, as the optimal solution.
As far as I know, no actual maker of slide rules had ever been bold enough to produce a slide rule with this type of arrangement. In one way, however, it is very conventional, in that the scales K A/B CI C/D are all in the same arrangement as on a 'Mannheim' slide rule, and the trig scales are even also on the back of the slider. The resemblance to the European Reitz slide rule is even closer, since the trig scales are of modern type, and the L scale has a typical placement for that type of rule: the Régle des Ecoles on the rear, the two R scales on the front, and the log-log scales, are all added to a typical modern Reitz-based layout without shifting even one scale of its original complement.
If, however, one is going to even begin to talk about how to design a slide rule, one very basic fact about how slide rules are used needs to be very well understood.
The diagram below shows how one would go about multiplying three numbers by the use of the slide rule, in the case where:
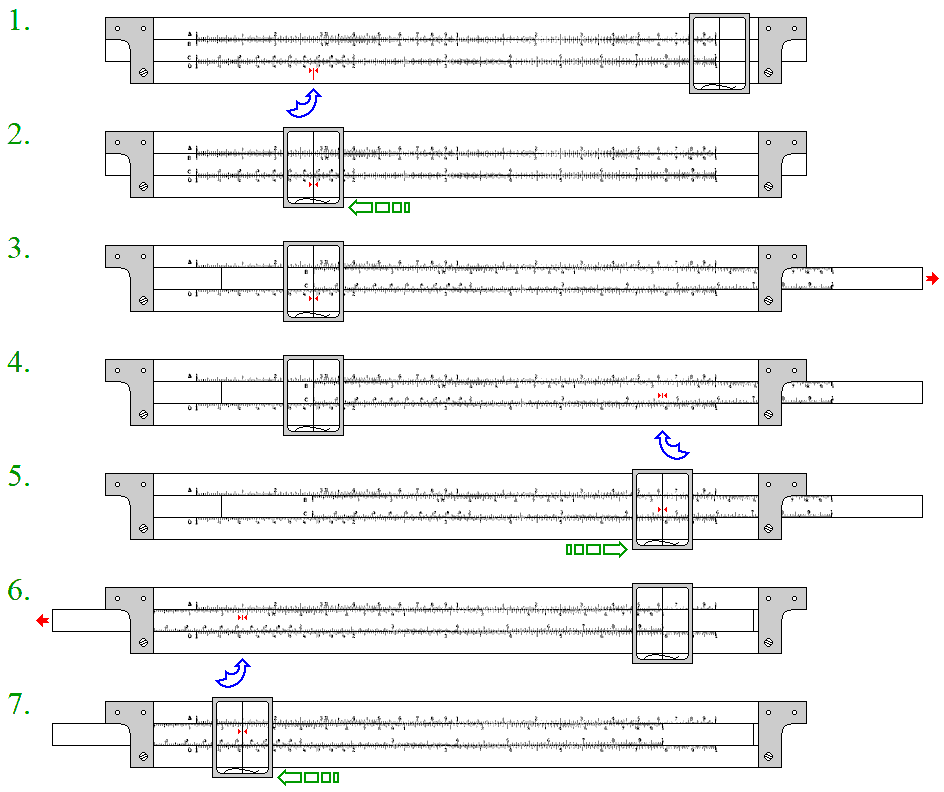
Step 1: We find the first number to be multiplied; it is on one of the scales on the stock of the rule.
Step 2: We move the cursor to that number.
Step 3: We move the slider, with the cursor to guide us, so that one of its indexes coincides with that first number to be multiplied on the stock of the rule.
Step 4: We find the second number to be multiplied; it is on one of the scales on the slider.
Step 5: We move the cursor to that number.
Step 6: (Actually, we are taking two steps here, to save a diagram which would not show much.) We move the slider so that one of its indexes coincides with the current position of the cursor, which is located at the product of the first two numbers. (The value of this product, of course, could be read on the D scale of the stock, assuming it is in its usual location.) And then we find the third number to be multiplied.
Step 7: We move the cursor to that number, and at this point, the product of the three numbers may again be read on the D scale by means of the cursor.
The point of the above is that between steps 2 and 3, and once again between steps 5 and 6, because our current value to be multiplied by a new number is on the stock of the rule, rather than the slider, we benefit from the fact that the cursor stays put on the stock of the rule when we move the slider.
If our current product was on the slider instead, we would have to read the value, and then move the cursor to that value after moving the slider; in addition to being an extra step, it introduces the possibility of additional error.
Thus, as a general rule, the slider is a better place for a scale on a slide rule than the stock. The slider is "premium real estate", if you will. This is why, for example, the S, T, and ST scales on slide rules are almost always on the slider instead of the stock.
But there are exceptions.
For example, the log-log scales are an exception. To raise a number to a power by the use of the log-log scales, one finds that number on the log-log scales, moves the index of the C scale to that number, then moves the cursor to the power on the C scale, and reads the result on the log-log scales. Since the end result is read on the log-log scales themselves, and they aren't used to find a place on the C (or D) scale with the result, which can then be multiplied by something else, they may as well be on the stock instead of the slide, thus saving space on the slide for scales that need to be there.
What about the hyperbolic trig scales? It would seem that the same argument as used for the regular trig scales applies to them, and yet they're nearly always found on the stock of a slide rule and not the slider.
Here, the reason is more complicated. It's not just that they were shunted to the stock of the slide rule because at this point, space on the slider had run out, and they were less often used, and so could get a less optimal place.
Instead, it's because the most common computation performed with the hyperbolic trig scales is to find the product of one conventional trigonometric function with a hyperbolic trig function, as part of evaluating a complex trig or hyperbolic trig function. No third factor will normally be multiplied by the result.
As a result, the fact that it's most convenient when multiplying two numbers if one is on the stock and the other is on the slider takes precedence over the fact that when multiplying three or more numbers, it's most convenient if all numbers, except the first one, are on the slider.
Another point about slide rules that might be considered is that when multiplying numbers, we move the index of the scale with the next number to be multiplied to the number we already have. But because we're using the C and D scales as our basis in multiplying, for the most accuracy, and not the A and B scales, there is always the question of which index to move, so that the next number to be multiplied will be located within the scales of the other part of the slide rule, instead of off to one side.
When dividing numbers, instead of moving an index to coincide with our current result, one is moving the new number to divide by to coincide with that result; and then the result of the division will be at whichever index of the scale with the divisor happens to be within the scale on the other part of the rule.
Given that multiplication is more common than division, and yet division seems to be easier and faster on a slide rule than multiplication, some people have designed slide rules where instead of a C scale in contact with the D scale, a CI scale is present, and the S, T, and ST scales are all replaced by their inverse or reciprocal scales.
However, this never caught on, presumably because it was perceived as too complicated or too hard to understand.