
Of course, conventional tilings need not be as simple as the illustrative examples provided on the previous page. Here, for example,

is an elaborate tiling from the Islamic world, which is famed for its achievements in geometric art. (This tiling belongs to symmetry class p2, incidentally. Also, in its original form, it was actually a frieze, that is, a pattern repeating in only one direction within a strip of finite width, and I have made certain assumptions in order to extrapolate it to a tiling.)
Here is another tiling, this one derived from an illustration within the famous Topkapi scroll:

Incidentally, that name may sound familiar. It is the name of a museum in Turkey, and in 1964 a movie was released about an elaborate plot to steal a valuable jewelled dagger from the museum. This movie served as an inspiration for the television series Mission: Impossible, where secret agents working on behalf of the U.S. State Department used similar techniques for good instead of evil. (In fairness, it should be noted that the movie Topkapi was a comedy.)
It appeared to me that the intended overall symmetry of the design was intended to follow this arrangement of the triangular and square areas (with the green stellated circles as the vertices):

thus, although the elements of the design lent themselves to a design with overall symmetry belonging to symmetry group p6m, an overall arrangement belonging to symmetry group pmm was chosen instead.
In drawing the larger diagram above of the actual pattern itself, I found I did not need to move the stars from their positions within the triangles when constructing the squares, although that theoretically means that the area within the square with apparent octagonal symmetry will not be perfect. This is because an angle of 24 degrees, resulting from the triangular and pentagonal angles in the way they interact in the diagram differs by only a slight amount from an angle of 22 1/2 degrees, that required for perfect octagonal symmetry. The diagram below illustrates this:
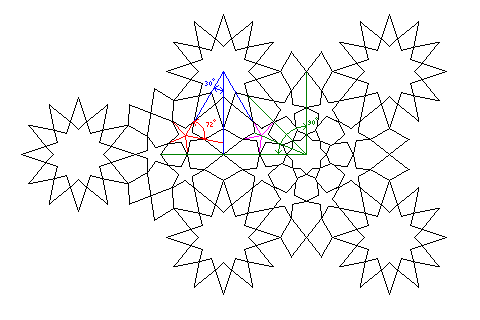
Divide a 90 degree angle into four parts, and you obtain an angle of 22 1/2 degrees, which is the angle at which one of the points of one of the stars on the right points above the vertical. The corresponding angle on the left side would be 60 degrees, from the triangular symmetry, minus 36 degrees, from the structure of the pentagon, yielding 24 degrees above the vertical.
This means that the pattern above appears to have some local symmetries that are, in fact, geometrically impossible to have simultaneously. However, to indicate what those symmetries are may take some explaining.
Since the triangular areas and the square areas in the pattern are independent, it is not in any way impossible
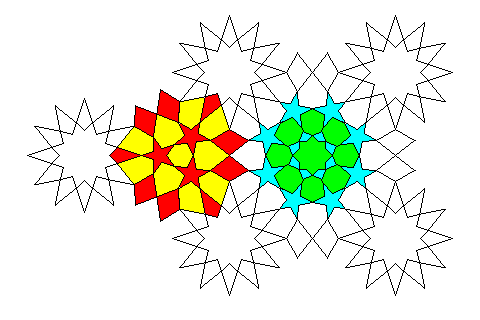
for the area inside the square areas shown in the diagram above in two shades of green to have perfect octagonal symmetry, and the area inside the triangular areas shown in red and yellow in the diagram above to have perfect triangular symmetry. In addition, of course, the stars are drawn here so as to appear to have perfect pentagonal symmetry, and it is certainly possible to arrange such stars at angles so that they are part of an overall pattern with either triangular or octagonal symmetry.
The symmetry that appears to exist that is in addition to what is possible is instead the bilateral symmetry shown below
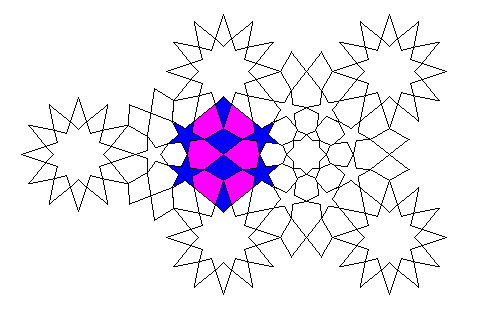
in the area shown in blue and purple. That is what is not consistent, but with only an error of one and a half degrees, with the simultaneous presence of the apparent symmetries in the other areas.
If one chooses to retain the bilateral symmetry, one can do so in two ways.
One is by starting from the triangular area, and copying from it to the square area; the result of that is that the inner part of the square area loses perfect octagonal symmetry.
The other is by starting from the square area, and copying from it to the triangular area; here, the triangular area keeps triangular symmetry, and so it is not the simultaneous octagonal, bilateral, and triangular symmetries that are inconsistent, but instead the consequence is that the three stars in the triangular area lose their pentagonal symmetry, becoming only bilaterally symmetric. In fairness, it should be noted that in the original drawing on the Topkapi scroll, the stars were not actually drawn so as to give an impression of perfect pentagonal symmetry.
The dodecagonal symmetry of the large circular areas shown in light green with their surrounding points also comes into conflict with the octagonal symmetry within the square areas, particularly when the pentagonal symmetry of the stars is involved. While the dodecagonal points and the points of the stars need not be pointing in exactly opposide directions, their location also causes problems. Thus, it seems the simplest way to draw this design will be to have the octagonal symmetry be broken by the one and a half degree discrepancy.