Basic Tilings: The 17 Wallpaper Groups

Another series of pages deals specifically with tilings that use either recursion or unusual matching rules to permit the construction of tilings with fivefold or eightfold rotational symmetry in an aggregate sense.

This page deals with the classical type of repetitive tiling. Such tilings can belong to one of seventeen different symmetry groups:

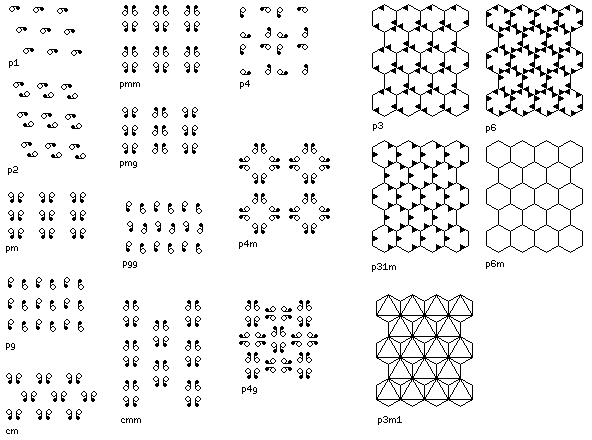
These symmetry groups have the following characteristics:

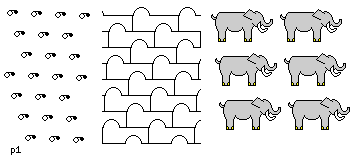
p1: This is most basic form of repetitive tiling, with the least possible symmetry; the only symmetry is that the tiling has a fundamental repeating unit, called a cell, which can be a general parallelogram.
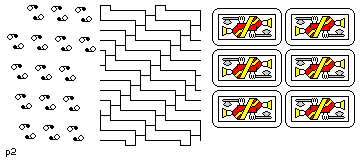
p2: Tilings of this type, in addition to having a repeating cell (as all the tilings discussed here must), can also be turned upside down and remain the same.
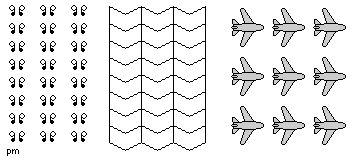
pm: This kind of tiling can be mirror-reflected along one axis. The cell must be rectangular or square in shape as a result.
pg: This kind of tiling has a glide reflection; this means that the tiling can be completely unchanged if it is both reflected and displaced at the same time. The cell must be rectangular or square in shape as a result.
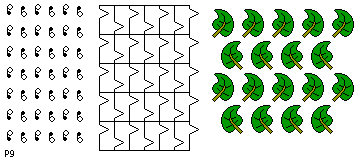
cm: This tiling has both reflections and glide reflections, the axes of which are parallel. The cell must be a rhombus (a parallelogram whose sides are equal) as a result.
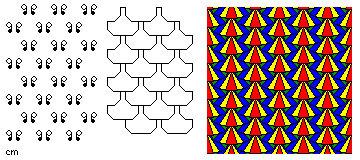
pmm: Here, there are two sets of parallel axes of reflection. The cell must be rectangular or square in shape as a result.
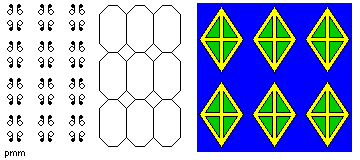
pmg: This kind of tiling has one set of parallel axes of reflection, and can also be turned upside-down and remain the same. As a result, it also has a glide reflection, and the cell must be square or rectangular.
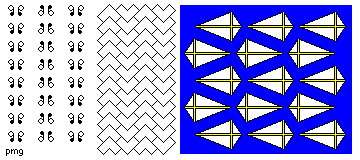
pgg: This type of tiling has glide reflections in two directions, and can also be turned upside-down. The cell must be rectangular or square in shape as a result.
cmm: This type of tiling has two sets of parallel axes of reflection, and can be turned upside-down and remain the same. There are some possible pivot points for turning the tiling upside-down that do not lie on an axis of reflection. The cell must be a rhombus (a parallelogram whose sides are equal) as a result.
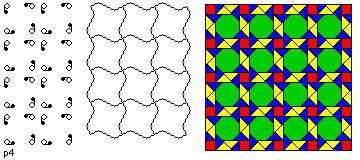
p4: This kind of tiling can be rotated by a right angle and remain the same. As a result, the cell is a square. There are also pivot points about which the tiling can only be turned upside-down and remain the same. It does not have any axes of reflection.
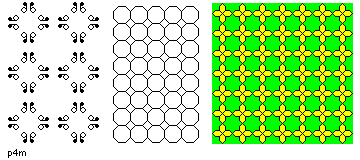
p4m: Tilings of this type, in addition to being able to be rotated by a right angle and remain the same, have four sets of parallel axes of reflection. The pivot points for every possible rotation, both those that offer right-angle rotations and those that offer only an upside-down rotation, lie on at least one of the axes of reflection. The cell is square.
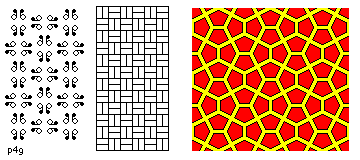
p4g: In a tiling of this kind, there are two sets of parallel axes of reflection. The pivot points for right-angle rotations do not lie on the axes of reflection; there are again also pivot points for upside-down rotations only, and these do lie on the axes of reflection. The cell is square.
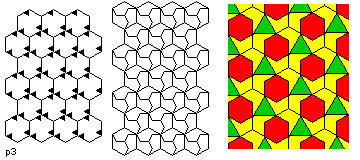
p3: In these tilings, the cell is hexagonal. They are symmetrical under rotations of 120 degrees, but have no reflections.
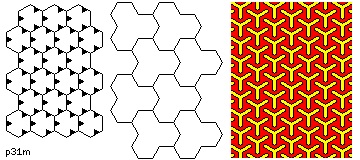
p31m: Again, the cell is hexagonal, and there are rotations of 120 degrees. As well, there are three sets of parallel reflection axes. The distinguishing feature of this type of tiling is that not all the possible centers of rotation lie on a reflection axis.
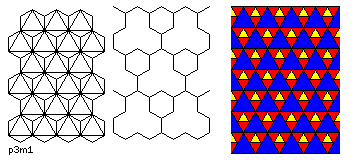
p3m1: In this type of tiling, the cell is hexagonal, there are rotations of 120 degrees, and three sets of parallel reflection axes. In addition, all the possible centers of rotation do lie on a reflection axis.
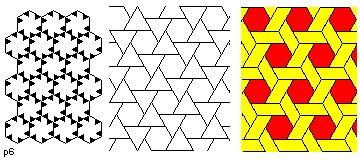
p6: Here, the cell is hexagonal, and rotations of 60 degrees are possible. There are also pivot points offering either only upside-down rotations or 120 degree rotations. There are no reflections.
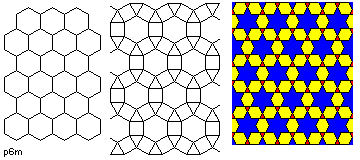
p6m: Here, the cell is hexagonal, and rotations of 60 degrees are possible. There are also pivot points offering either only upside-down rotations or 120 degree rotations. There are six sets of parallel axes of reflection, and the centers of 60 degree rotations are on these axes.

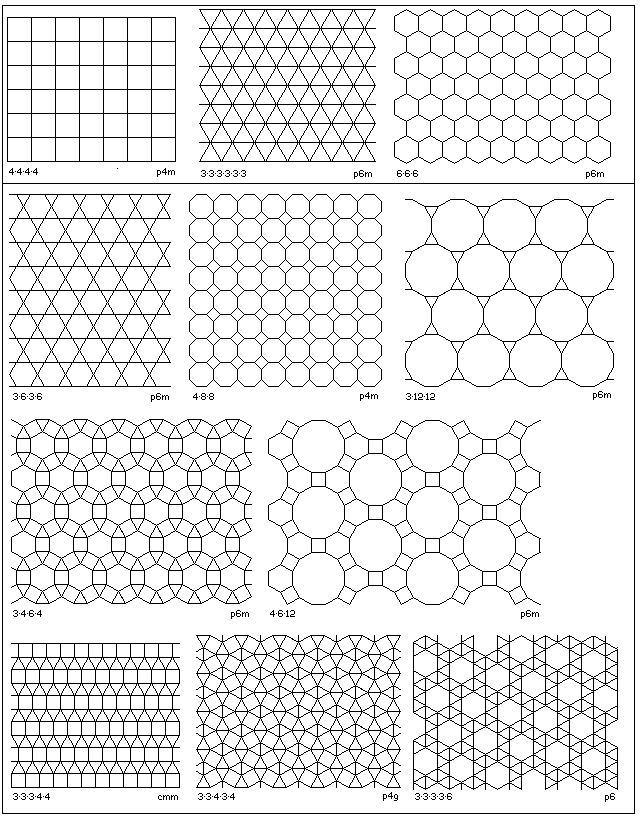
Below, the 11 Archimedean tilings, as enumerated by Kepler, are shown. (The three on the top perhaps would be better called the Platonic tilings, by analogy with the polyhedra.) Note that only five of the symmetry groups, p4m, p6m, cmm, p4g, and p6, are represented among them.