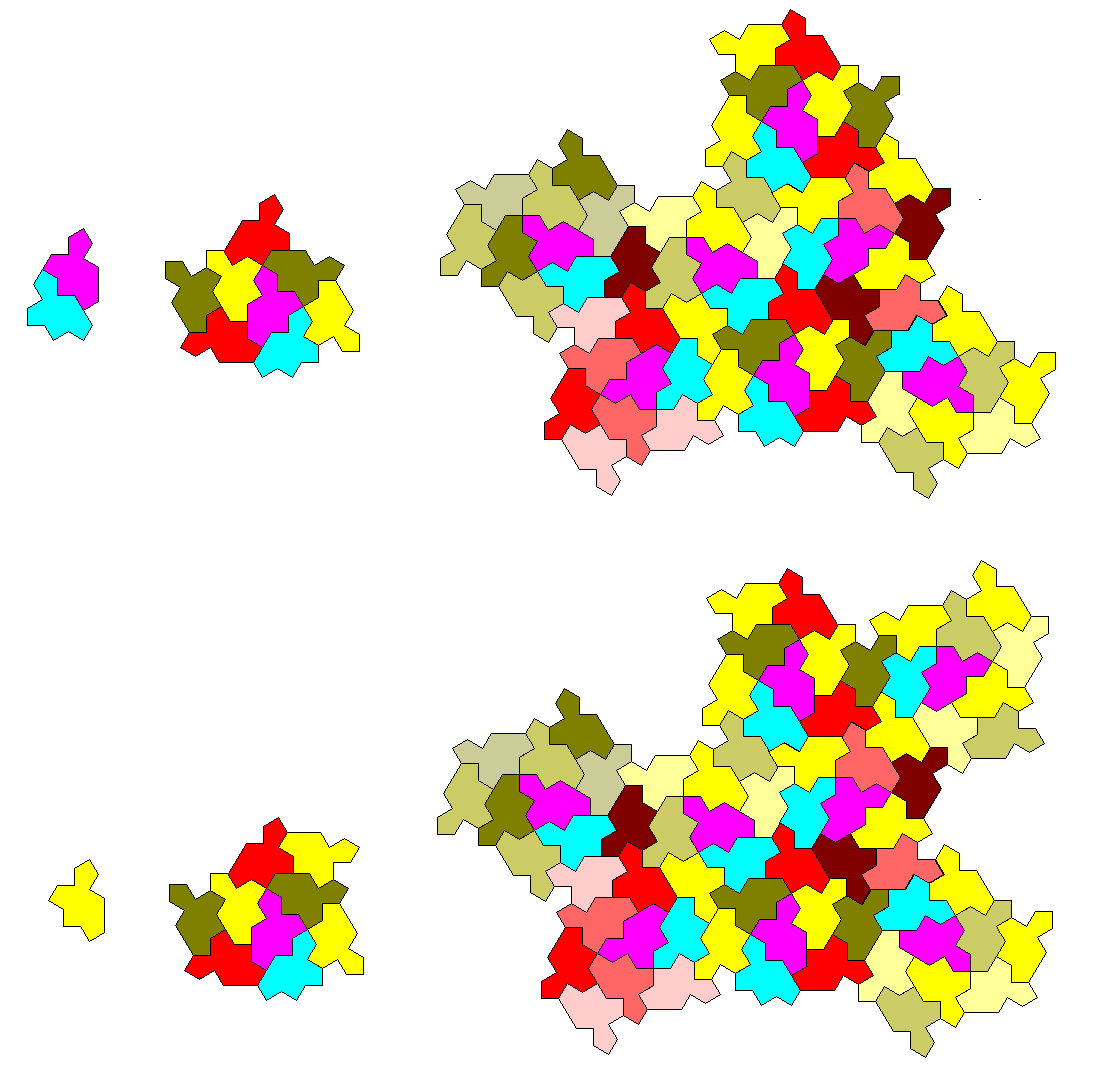
A later page begins a series on using either matching rules or recursive tiling to achieve tilings with aggregate fivefold or eightfold symmetries, symmetries that can only be fully achieved around a single point at best, but which can be achieved in a partial sense around an infinite set of points in a tiling if that tiling is a suitably-arranged aperiodic tiling.
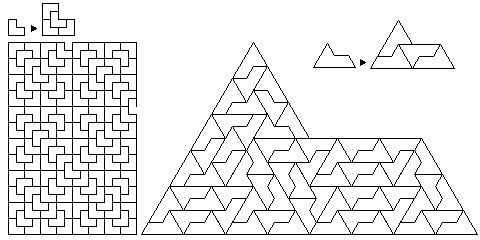
Recursive tiling need not generate novel symmetries. Here are a couple of recursive tilings that operate within the lines set down by a conventional square or triangular tiling:

Recently, an aperiodic tiling involving two tiles, and matching rules for those tiles, was derived from the first of these two simple recursive tilings by Chaim Goodman-Strauss. The two tiles used are called the trilobite and the cross, and the matching rule involves not colored areas that touch along a line, but rather those that are on opposite sides where four of the sharp points of the pieces meet.
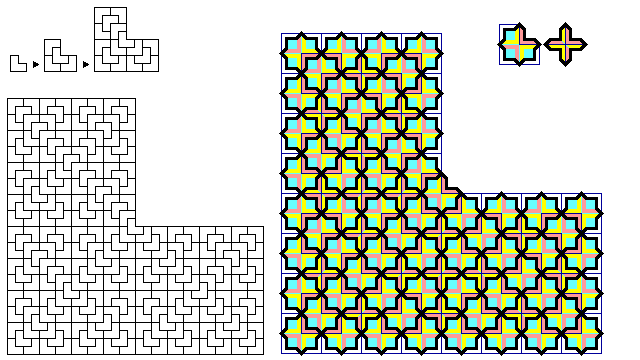
The image above is an attempt to make the boundaries of these tiles clearly visible despite the way in which the colors of the tiles tend to obscure those boundaries; also, it has been intended to make the relationship to the previously-known L-tiling apparent.
An alternate set of tiles that can produce the same tiles with conventional color matching rules is shown below:
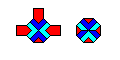
The first tile replaces the trilobite, but the second tile replaces not only the crosses, but also the places where the sharp corners of four tiles meet. The proof that this tiling is equivalent to the trilobite and cross tiling was quite difficult.
The diagram below shows two sets of six tiles whose matching rules lead to aperiodic tilings. The top row shows the six tiles for the Robinson tiling, the bottom row shows the six tiles for the square Ammann tiling. These tiles can be reflected and rotated; for the Ammann tiling, only one piece needs to be able to undergo 90 degree rotations, the last one.
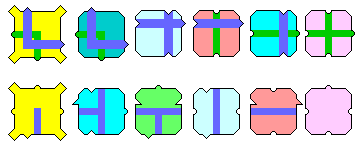
Here is the Robinson tiling which achieves an impressive aperodic structure:

This tiling was described in a paper published in 1971, one year before the publication of the Penrose tilings, and this was the first tiling known which forced aperiodicity with only six tiles.
And this is the square tiling due to Robert Ammann, who also devised the Ammann-Beenker tiling with octagonal symmetry, as well as several other tilings of different kinds:
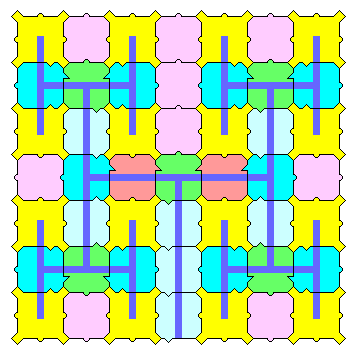
Another tiling devised by Robert Ammann is this one, in which the ratios between sides of different length of the pieces are the golden ratio or its powers:

An attempt has been made to show a large extent of this tiling so that a subtle characteristic of it might be visible: the density of smaller tiles, shown in yellow in this diagram, varies along directions characteristic of pentagonal symmetry. This is an example of a phenomenon known as Ammann bars, which will be discussed in the case of the Penrose tiling later on.
Note that despite its reflection symmetry about a diagonal, the smaller tile is reflected instead of rotated by 90 degrees for purposes of recurrence. This is not merely laziness on my part in the use of the paint program with which I have drawn these images, it is actually how the recurrence relations work for this tiling.
Very recently, at least as I write these lines, a revolutionary discovery has been made of a tiling in this class.
In the paper An Aperiodic Monotile, David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, mathematicians from the United Kingdom, Canada, and the United States, announced the discovery of a single tile the shape of which forces an aperiodic tiling.
The conventional tesselation on which these tiles are placed looks like this:
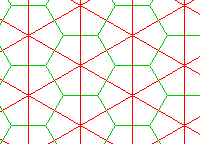
The plane is first divided into equilateral triangles, and each triangle is divided into three parts.
The shape of the monotile which has this property is shown below, by the shaded spaces within this tesselation:
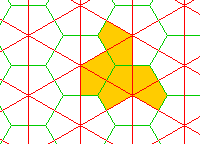
The monotile has been nicknamed a "hat" because of its shape.
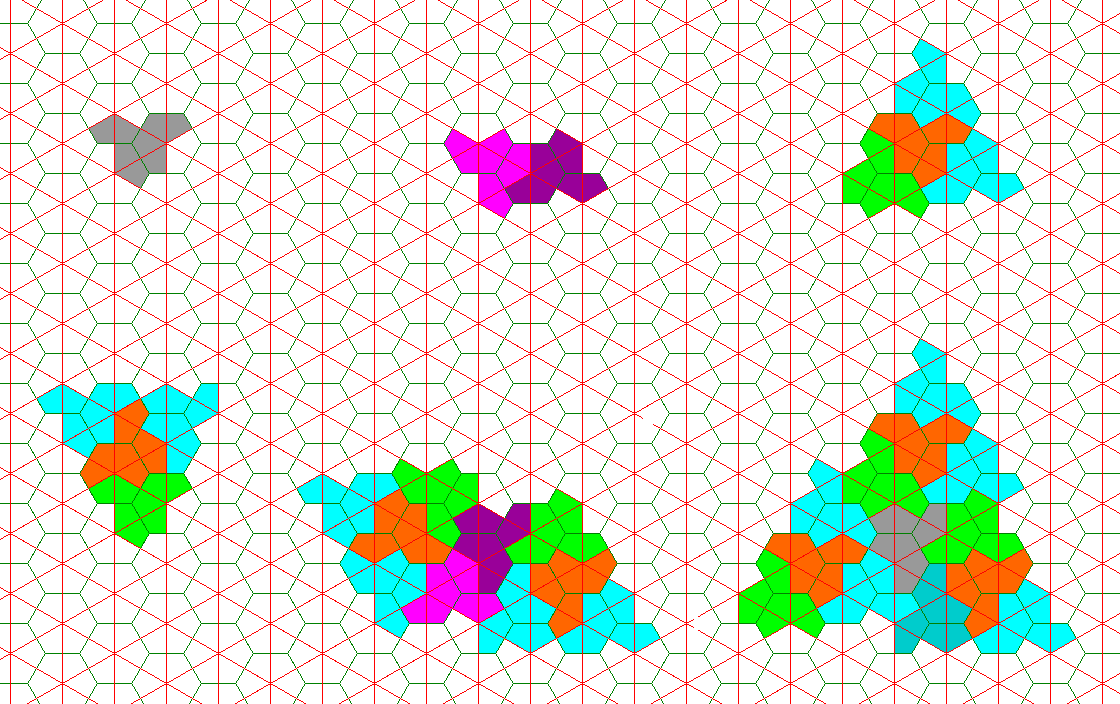
And here is a small piece of a tiling constructed according to the matching rules set forth for this type of tiling:

Assistance from a computer was required to construct the proof that this shape could only tile the plane in an aperiodic fashion.
The team had also discovered a second aperiodic monotile, which they have dubbed the "turtle":
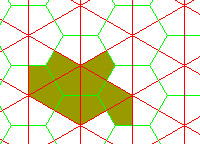
Note also that in both cases, both the tile shape and its mirror reflection are required for an aperiodic tesselation.
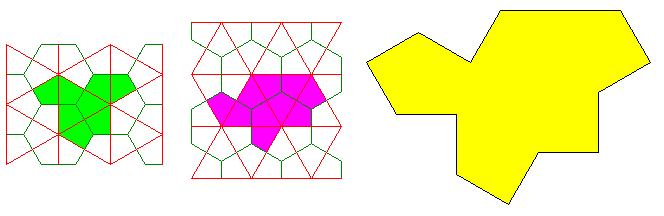
The aperiodic tiling based on the "hat" can be expressed in terms of a recurrence relation. The diagram below shows how this recurrence relation is based on three shapes which are built from multiple pieces:
However, it is not a complete depiction of the recurrence relation. The shapes in the top row aren't simply expanded into the larger shapes corresponding to them in the bottom row; also, a layer of the second small shape in the top row is placed between the shapes in the bottom row to form the next generation of the tiling.
Subsequently, the same team of researchers has discovered a true aperiodic monotile, which tiles the plane aperiodically without requiring a reflection of the shape to be present. This shape does not fit within a periodic lattice, but it is related to both the "hat" and "turtle" shapes noted above, as shown in this image:
This shape was dubbed the "Spectre". The diagram below almost shows its recurrence relation:
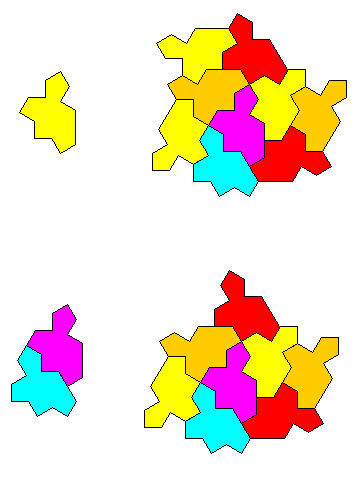
The bottom of this diagram shows the recurrence for a particular symmetric combination of two Spectres, dubbed the "Mystic". All other Spectres move to the next generation according to the recurrence in the top of the diagram.
The reason I say that this diagram almost shows the recurrence relation is because the tesselation also has to be mirror-reflected at each step in the recurrence.
This reflection can be made visible by showing two steps in the recurrence: