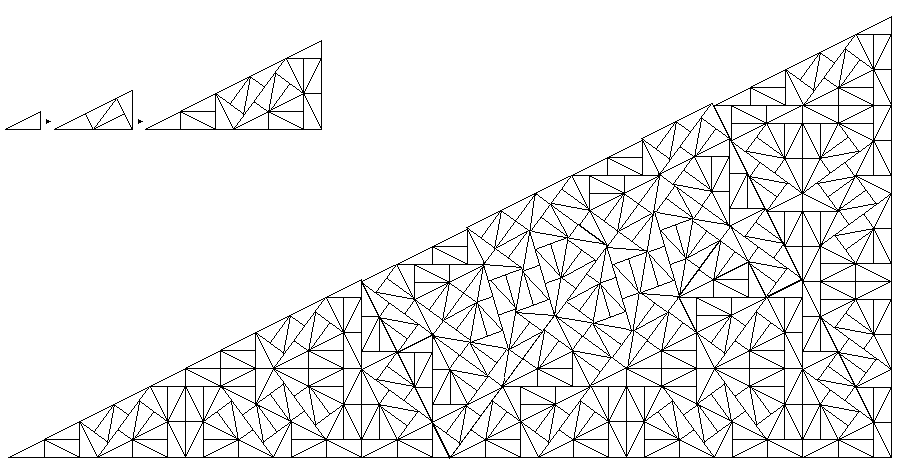
On the other hand, this tiling, the pinwheel tiling devised by J. H. Conway (famous as the inventor of the cellular automaton game of Life)

working with a right triangle with sides of 1, 2, and the square root of 5, produces lines going arbitrarily close to any direction if continued for a sufficiently large distance.
This diagram brings out the recurrence relation of the tiling more clearly:
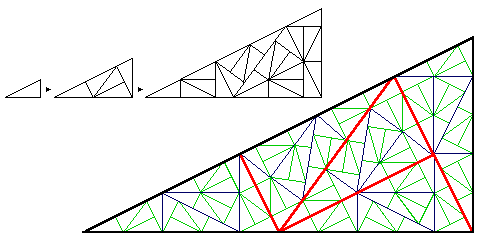
And this diagram illustrates how higher and higher multiples of the angle which is the arctangent of 1/2, which is not a rational fraction of a circle, are gradually introduced in this tiling:
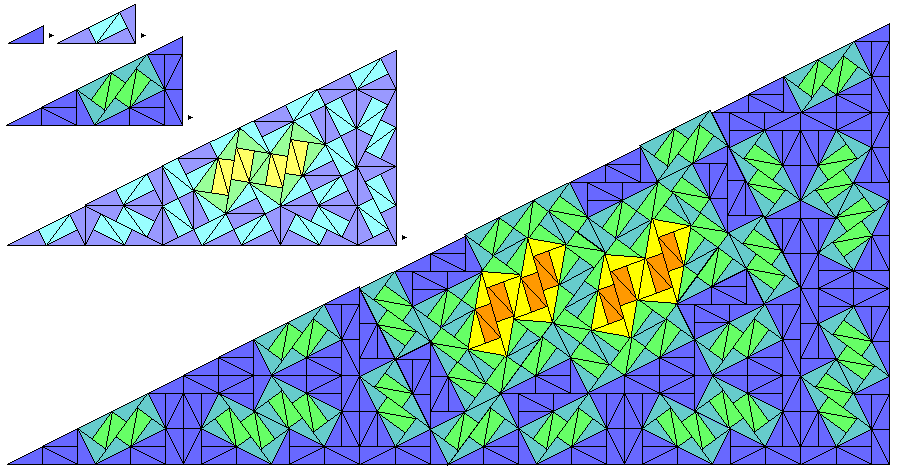
Incidentally, it was Lorenzo A. Sadun who proposed that the pinwheel tiling could be generalized to other right triangles if one allows a tiling with different sizes of triangles in it:
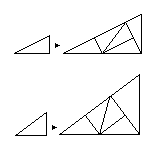
In the diagram, the original 1:2:sqrt(5) triangle is shown, with a different triangle, the 3:4:5 triangle, below it. The two acute angles are still not integer parts of a circle; triangles whose angles are integer parts of a circle could also be chosen, to create triangle tilings that could be the basis for tilings with any desired order of symmetry.