
There are various techniques which can be used to produce a pattern with pentagonal symmetry.
One is to use tiles with special rules (or jigsaw puzzle-like keyed sides) for joining. This produces a Penrose tiling. Although these tilings are covered by U. S. Patent 4,133,152, this patent, granted on January 9, 1979, has expired. This has apparently happened without producing a flood of cheap toys based on these tilings, but that is more of a comment on the intelligence of public taste than on the merits of these tilings.
The Penrose tilings will be discussed on the next page.
It is also possible to make a fractal tesellation, with different sizes of pentagons, down to the infinitely small, which consists of nothing but pentagons. This is illustrated by the faces of Dodecafoam, a three-dimensional fractal tesselation of dodecahedrons.
A less impressive technique, but still capable of drawing inspiration from the other two, is called substitution tiling.
Here is part of my first attempt at such a tiling:

In trying to make a tiling which is mostly composed of pentagons, the first step, with this technique, is to try to build larger and larger pentagons which are mostly composed of the small pentagon one starts with. This can be done fairly well, as this diagram shows:
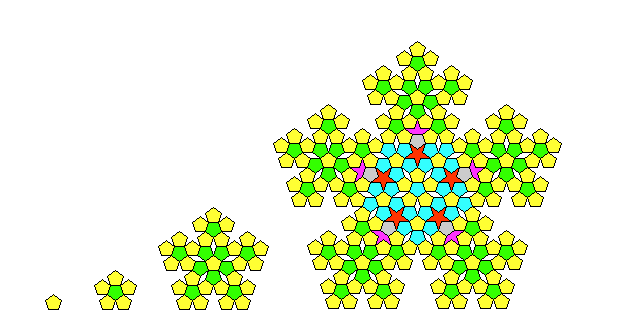
On the smallest scale, one has one pentagon.
Next comes five pentagons, surrounding a sixth one in the centre. There are small wedge-like gaps on the edges.
If one takes that larger pentagon, and forms a yet larger one by substituting the larger pentagon into itself, replacing its component pentagons by its original shape, one gets the next larger pentagon. Some of the wedge-like gaps have now paired to form an additional tile, a small diamond, that we will need in addition to a pentagon.
Repeating this again, one gets the next larger pentagon. In addition to wedges, this has two other component shapes: a star, and an incomplete star which I originally called "hat" on these pages, but which Dr. Penrose termed a "boat" when he described the first of his famous aperiodic tilings; thus, I shall yield to his term. Those two shapes could be built up from five and three diamonds respectively, but I thought having them as additional tile types would look nicer, even if it made the tiling more complex.
Only one more basic tile type remains to be seen.
So far, we have repeated the process of expanding the pentagon only a few times. In addition to replacing the pentagon by a bigger version of itself, in the last iteration, we replaced the small diamonds by a bigger version of themselves, composed of a boat, a pentagon, and a star.
As we repeat the process further, we will need even larger versions of the diamond, and this illustration shows some of them:
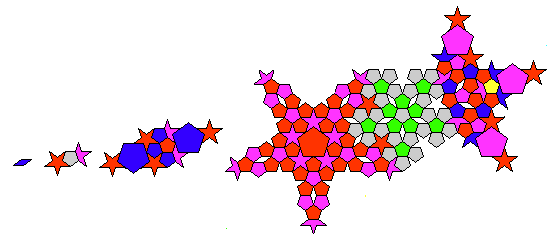
Note that the fifth basic tile shape makes its appearance in this diagram. It is a larger pentagon, with each side exactly twice as long as the sides of the original pentagon.
To be able to continue this process indefinitely, we need larger versions of the double-size pentagon, the star, and the boat, as well as the diamond and the pentagon.
This illustration shows these: note that for these shapes, unlike the diamond and the pentagon, there are no equivalents after only one enlargement step. But there is an equivalent for each one after two enlargement steps, and because of the way in which the internal components of the larger equivalents of the diamond are rearranged, one simply switches to using a different version of the diamond as the base when enlarging one step, instead of attempting to replace all the diamond's internal components by enlarged versions of themselves in one step instead of two.
Thus, we do have a usable recurrence relation, even if a complex one, since the basic shapes that contain double-sized pentagons are the boat and the star, and one-step enlarged equivalents for them are given.
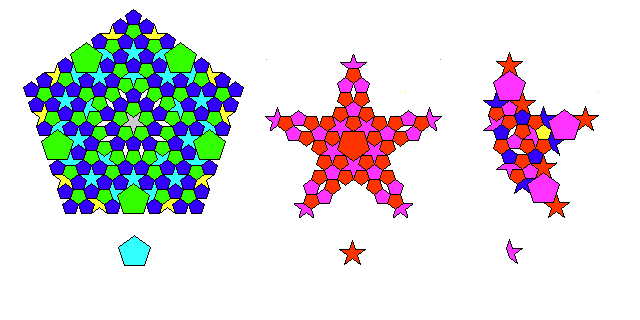
Now, here is the full tesselation. It shows to what distance one must go to encounter an enlarged double-size pentagon.

Finally, an incomplete diagram on a larger scale, with only the once-enlarged diamonds filled in.

This illustrates the fractal nature of this tesselation, although it is fractal only upwards, not downwards as shown here, unlike Dodecafoam, which is a true fractal. Also, it illustrates that the larger pentagons only create diamonds; thus, we do have a choice which order of diamond to use, and so the lack of once-enlarged boats, stars, and double pentagons is indeed not a problem, as claimed.
Designs of a simpler nature using pentagons had been devised long before by Dürer. These could be put in an overall pattern having pentagonal symmetry, like the following:
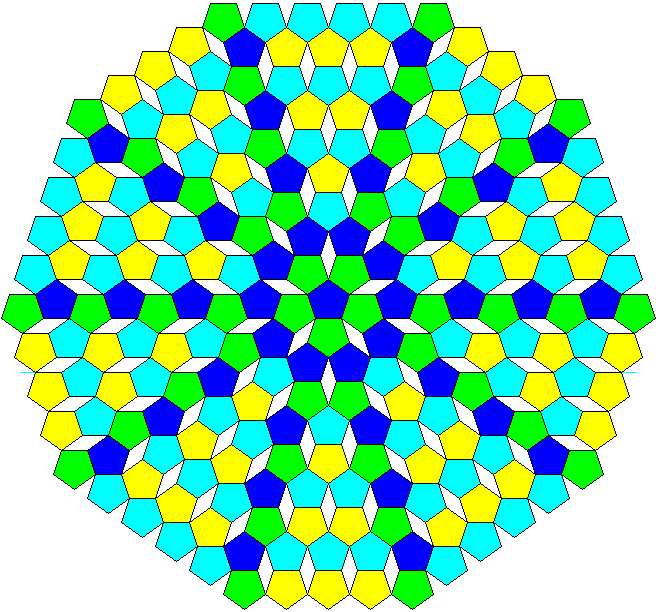
but as you can see, the parts that are repeated are not pentagons: rather, a rectangular cell is being repeated, although in five directions in this case.
At about the same time, Kepler, who corresponded with Dürer, experimented with arrangements of pentagons, and some of his drawings in Harmonia Mundi are strongly suggestive of the original Penrose tiling with six pieces. However, just as neither Emil Mackovicky nor Peter J. Lu have quite found unequivocal evidence that a truly quasicrystal-like tiling, such as a substitution tiling, was produced in the Islamic world, although the evidence does show that at least very tantalizingly close approaches had been made, while I have been referring to substitution tilings as "Keplerian" tilings here, no substitution tiling with pentagonal symmetry appears to have preceded Penrose, despite it appearing that a substitution tiling would have been much simpler to devise than one with matching rules.
One published paper, available on the web in in more than one form, has inferred from one of the patterns in Harmonia Mundi, that that pattern formed part of the tiling of the Dürer type shown below:
