The picture below is a picture of a pile of cubes
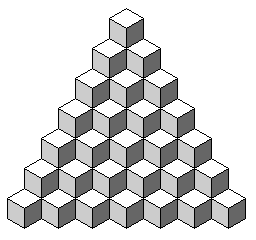
but part of it is also a picture of a tesselation of rhombs.
If one takes a grid of squares, and instead of removing squares to make a 45 degree angle, we remove squares so as to make a slope whose arctangent is the reciprocal of the golden ratio, we can have the squares at the top alternate between one square and two squares with the same pattern as the "musical sequence" that led to the Ammann bars for the Penrose tiling, as this diagram illustrates:
The following diagram illustrates a cube, drawn using lines taken from a Penrose rhomb tiling, whose outline is in black, followed by a four-dimensional hypercube, where red lines in the direction of the fourth dimension join the original cube in black to another cube shown with a dark green outline, followed by a portion of a five-dimensional hypercube, where we also show a cube displaced along the fifth dimension in blue, joined to the original cube by light green lines.
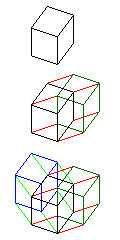
The choice of lines from the Penrose rhomb tiling means that many of the lines in the diagrams coincide, making this a less clear illustration of the fifth dimension than might typically be drawn. The third drawing omits the cube displaced along both the fourth and fifth dimensions that would be needed to make it a diagram of a five-dimensional hypercube:
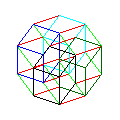
Note that because hidden lines of the 3-dimensional cube components are omitted, these diagrams have fewer lines than a diagram of the hypercube usually has.
If we use the convention chosen for that diagram as a guide for coloring a Penrose rhomb tesselation, we might get the following:
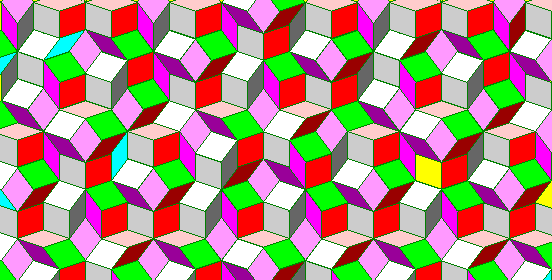
The three rhombs that represent faces oriented within the conventional three dimensions are colored white, light gray, and dark gray, the three rhombs that represent faces with one edge directed in a three-dimensional direction, and another edge extending into the fourth dimension are colored light red, red, and dark red, the three rhombs that represent faces with one edge directed in a three-dimensional direction, and another edge extending into the fifth dimension are colored light purple, purple, and dark purple, and finally the rhomb whose edges are directed in both the fourth and fifth dimensions are colored green.
Although this looks pretty, it doesn't seem to provide much in the way of insight into any relationship the Penrose tiling might have to five-dimensional space.
This diagram
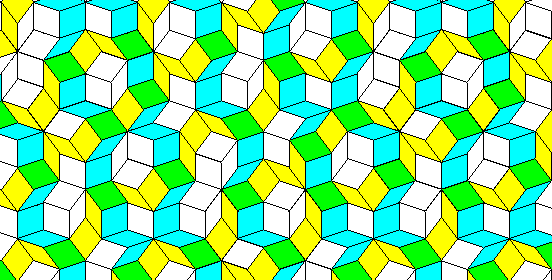
perhaps begins to suggest such a relationship. The chains of rhombs that mark an advance into the fourth dimension are shown in light blue-green, those that mark an advance into the fifth dimension are shown in yellow, and the tiles where these chains cross are shown in green.
Thus we see a link between the fact that this is a tiling of rhombs and the ability to consider it as connected with a higher-dimensional space; since every rhomb has pairs of parallel edges, each possible edge direction can be thought of as an advance in a distinct direction that has to be made in an organized, consistent manner; that is, positions along all five dimensions for the vertices of a Penrose rhomb tiling is necessarily transitive, which lets us think of each of the five possible line directions as belonging to an independent dimension instead of merely being a displacement within the two-dimensional tiling.
Although the chains meander considerably, the two families of chains shown each have their own linear trend. In addition, these chains, unlike Ammann bars, seem to have a uniform spacing. This would make sense if these chains result from applying a uniform slope to a regular stacking of five-dimensional hypercubes. As with the diagram showing the relationship of Ammann bars to an array of squares, the spacing may increase or decrease around a constant average.
We are gradually approaching an explanation of the technique that lets programs such as Quasitiler and DSA Gridmethode and QuasiG start from five sets of parallel lines and produce a Penrose tiling.