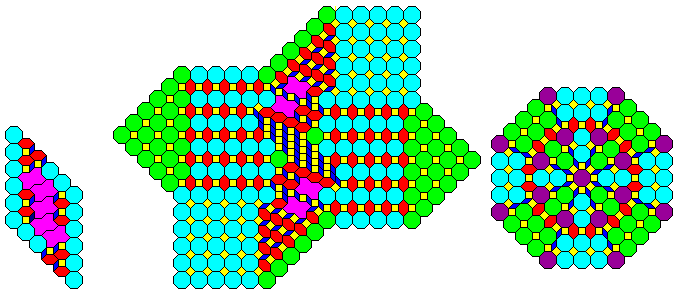
Oh, yes: I finally came up with a recurrence relation suitable for creating a Keplerian octagonal tesselation.
Unlike the recurrence relations shown for the Keplerian pentagonal tesselation, here the outer row of octagons belonging to adjacent pieces overlap. This applies to both those shown with a color, and those left blank.
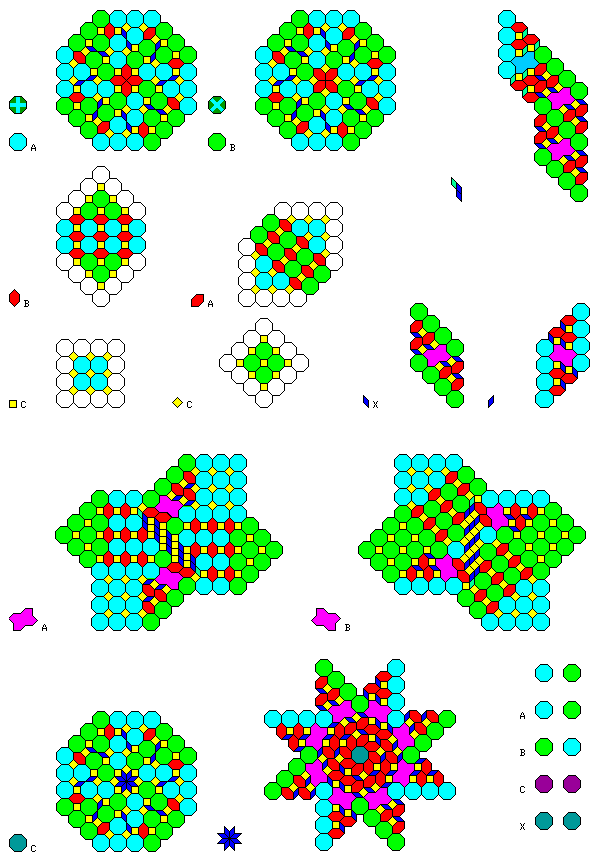
Green is used for octagons mainly connected to adjoining octagons diagonally, blue-green for those connected to adjoining octagons orthogonally; the slight difference in the center allows overall symmetry to be maintained. It was originally intended that when a green octagon overlaps a blue-green octagon, the deciding criterion will be the direction in which the higher-order octagons are connected; but since there are also fully symmetric octagons, depicted in a light blue color, using them in such a case instead, allowing the occasional recurrence of that shape in the design, is to be preferred. This only applies when an octagon overlaps an octagon; diamonds have unconditional priority over octagons, and octagons have unconditional priority over wrenches, hexagons, and other shapes.
The difficulty in creating a recurrence was primarily located in the diamond piece, shown as blue. In order to allow it to be created, a new piece, which I will call the wrench, shown in purple had to be defined. Note that the non-octagon pieces in the outer row must override the octagons they overlap on adjacent pieces. Inside the recurrence relation of the purple piece, the three diamonds connected by a sheared L-shape are not impossible, but they require that one of the component diamonds be reflected along its long axis so that non-octagons only overlap with octagons, as illustrated in the upper right of the illustration.
The recurrence rules shown in the bottom row of the diagram, although of a supplementary nature, are required in order to provide a tesselation that actually does have overall eightfold symmetry.
Starting from one of the two octagons at the top, and applying the recurrence rules in all but the bottom row of the chart, which are sufficient to tesselate space, leads to a pattern the overall symmetry of which is still only quadrilateral. This is true for two reasons.
The symmetry of the octagons at the top is only quadrilateral, and none of the other shapes has more than quadrilateral symmetry. Thus, the third octagon shown at the bottom, with true eightfold symmetry, can be used as an appropriate starting point.
The colors of the green and blue-green octagons will be distributed in such a way as to reduce the symmetry of the original pattern to quadrilateral symmetry as well. One way of dealing with it would be to use a + and X pattern to distinguish the two types of octagon, so that a 45 degree rotation would switch colors; this is shown in the diagram. Another way, when colors are used as a guide to setting actual colored tiles, instead of as a guide to the recurrence relation, is to use a special set of rules for tile colors. One such set of rules is shown in the lower right corner of the diagram. The border octagons, shared by two larger-order tiles, have their own special color, shown by rule X, which is given as the rule applying to the diamond, which has only border tiles. The small squares have their own color, shown in rule C. As for the other shapes, depending on their orientation, they either follow rule A, where the blue-green and green colors remain as used to indicate recurrence, or rule B, in which they are reversed.
Incidentally, since one of the diamonds of the three that make up the sheared L-shape is a reflection of one normally used with a rotation of 45 degrees from its orientation, while this is not strictly necessary for eightfold symmetry, it would seem appropriate, where this shape occurs in the higher-level portion of an arrangement, for the internal arrangement of pieces within its central wrench piece to be reversed as well. This is illustrated in the diagram by using a light blue color for parity-reversed diamonds, and a light purple color for parity-reversed wrenches. The component diamonds within an enlarged reversed diamond could also be reversed.
The complete set of rules in the diagram above leads to a pattern like this:

and, of course, one other pattern with octagonal pinwheel symmetry is possible by applying these recurrence relations:
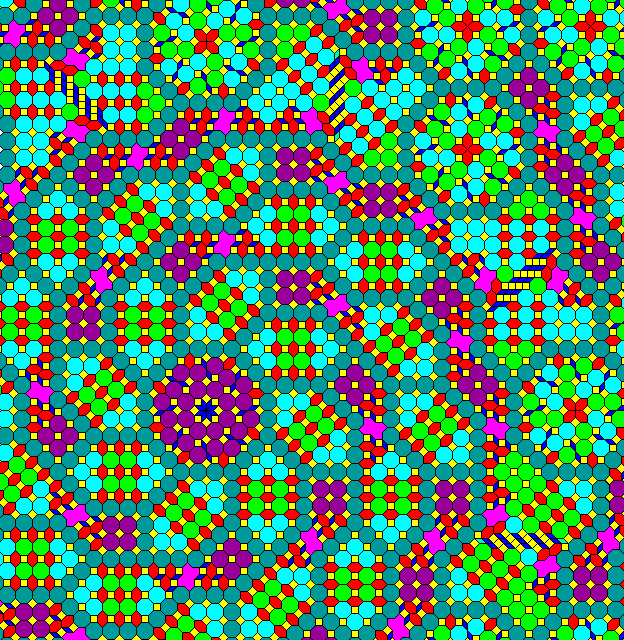
Patterns with other symmetries are possible starting from other pieces in the center of the diagram and applying the recurrence relations successively, and the rules of this particular recurrence relation can also be modified in a number of small ways, such as the rules governing the placement of reflected diamonds and wrenches, or the rule for octagons of opposite color overlapping from parent octagons which is noted as affecting an important fundamental property of this type of tiling.
The diagram below illustrates some other ways in which to vary this basic type of tiling.
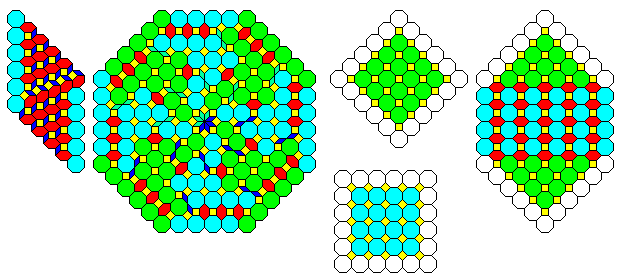
The basic pieces are enlarged; the enlargement of the octagon follows the pattern of an earlier octagonal tiling of the simpler Goethe type, and the others are easily enlarged. Also, the diamond piece is modified in a way that allows dispensing with the less-symmetrical wrench piece. But there is a cost in terms of the internal symmetry of the pieces making up the enlarged diamond. Because one of the border octagons is lost, the diamonds making up the central pinwheel must be oriented so that all non-octagons overlap an octagon, and because of the loss of symmetry, a rule for orienting diamonds needs to be adopted. Note that the method used for eliminating the wrench piece is applicable to the original smaller-scale tiling as well.
The original tiling appears to be better from an aesthetic point of view, however. But one interesting possibility suggests itself. Since the component pieces may all be easily enlarged, performing the recurrence so that at each larger scale, a larger size of component unit is also used, would produce another type of tesselation still having octagonal symmetry. As there is a Goethe tiling of pentagons, it is possible to do the same for a pentagonal tesselation as well.
If one would like to use the wrench piece in the enlarged diamond, it is also possible to enlarge the wrench piece; also, note that an octagon whose side includes an odd number of octagons is not only possible, but can be made more symmetrical than the octagon used previously: