A conventional tiling of squares is possible, and one of octagons alternating with squares with fourfold symmetry. Similarly, a conventional tiling of hexagons is possible, and one can also replace each hexagon with a dodecagon, leaving a triangle where the now-truncated corners of the hexagons met.
If, therefore, aperiodic tilings with octagonal symmetry are possible, then might aperiodic tilings with dodecagonal symmetry also be possible? Indeed they are.
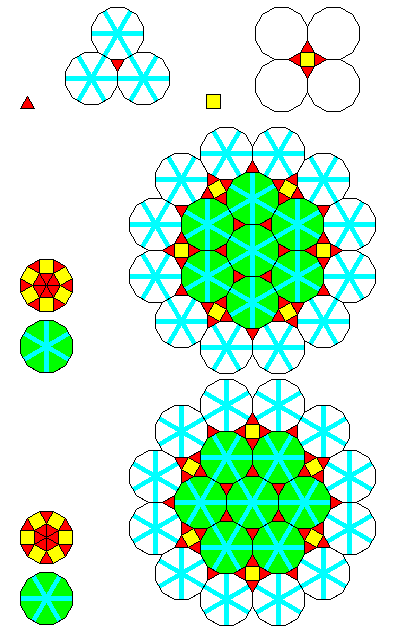
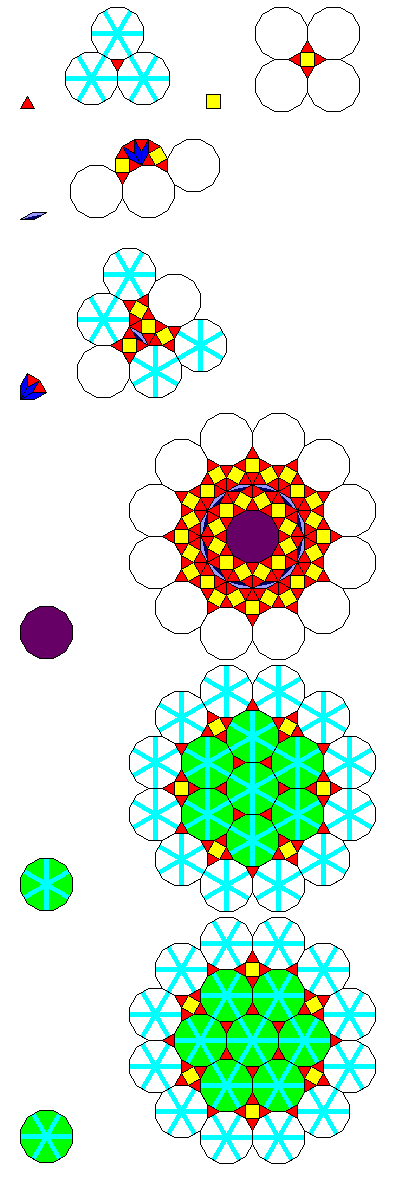
One obvious recurrence relation for a Keplerian dodecagonal tiling is shown below:
In one generation of the recurrence, vertices usually become dodecagons, except when they are too close together, as occurs in the case of the obtuse angles of the rhombs. So, as with the octagons on the edges of the shapes given in the recurrence relations for the octagonal tilings, where dodecagons overlap that are uncolored, a dodecagon fills the space except where an obtuse angle from a rhomb forces the area to be broken up into other tiles.
Note that in the recurrence rule for the dodecagon, and in fact even in the recurrence rule for the single rhomb, some dodecagons are unnecessarily broken up into other shapes. The reason for that, however, may be obvious to some viewers. Its purpose is so that the recurrence relation fully preserves the symmetry of each shape.
It would clearly be possible, through setting up more complicated rules, to establish a way of placing additional dodecagons where possible in such a way as to preserve dodecagonal symmetry.
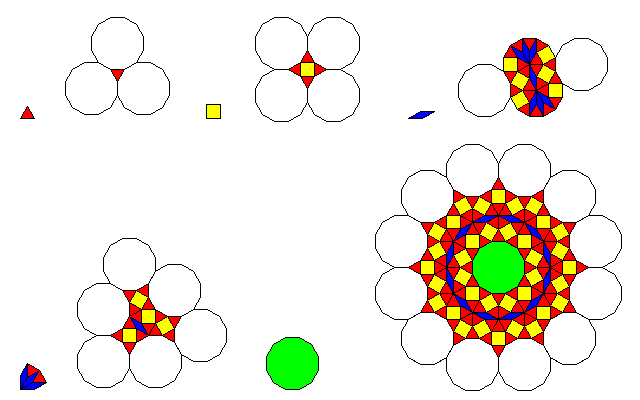
Because the recurrence relation for the rhomb forces rhombs to occur with obtuse angles touching, a special rule for this case was required. Note that an arrangement is shown corresponding only to the specific case needed, three adjacent rhombs. And the triangles, which are the only pieces that can fit into the spaces between the rhombs, are also included in the recurrence.
One can easily enough derive an arrangement for two adjacent rhombs from the pattern of a single rhomb, as shown in the first part of the diagram below:
But when attempts are made to simplify the design, by using dodecagons where it is possible to do so and maintain the symmetry of the parent shape, the resulting possibilities, shown as the second and third possibilities in the diagram above, do not lend themselves to being combined to form a recurrence rule for three rhombs, and thus that case had to be dealt with directly.
And here is an example of the tiling produced by these recurrence relations:

In addition to having overall general twelvefold symmetry, the tiling can have perfect twelvefold symmetry about one center, by beginning with the dodecagon and repeating the recurrence relation from that shape.
Incidentally, if six of the possible locations where smaller pieces can be replaced by dodecagons are used in the expansion of the dodecagon, it would be possible to modify this tiling so that the rhomb is excluded completely. But then the expansion of the dodecagon would only have the sixfold symmetry of a hexagon. It may be possible to alternate the two possible orientations of the expansion of the dodecagon to retain true twelvefold symmetry.
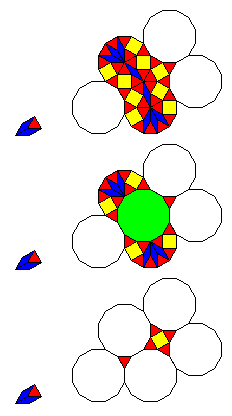
A recurrence relation envisaged to achieve this in part at the cost of only limited additional complexity is illustrated below:
When the unfilled dodecagons from two pieces overlap, if some of them indicate an orientation, then the orientation of the dodecagon to be placed in that space after a recurrence is determined by two rules:
Where no orientation is indicated, either by the absence of an oriented dodecagon in the overlap, or by a tie between the two orientations, then the original neutral dodecagon with full twelvefold symmetry is used.
Note that rhombs also have orientation, but this is always unambiguously indicated.
This attempts, with a minimal amount of additional complication, to reduce the number of times a potential dodecagon is broken down into smaller shapes. It may be possible, with rules that are considerably more complicated, to eliminate the divided dodecagons completely while still retaining full twelvefold symmetry in some sense. If that is the case, since a dodecagon itself can be broken down into only triangles and squares (with a similar loss of symmetry), the possibility of a twelvefold-symmetric tiling using only those two shapes is suggested, and indeed such a tiling is exhibited in the paper "What is Aperiodic Order" by Baake, Grimm, and Moody. One might then consider taking the square and triangular shapes from the particular tiling within the Topkapi scroll illustrated on an earlier page, and arranging them according to such a tiling, to bring in both pentagonal stars and areas with square symmetry that miss out on octagonal symmetry by only one and a half degrees. Since that tiling prominently features serrated circles surrounded by outward-pointing kites with twelvefold symmetry, using its elements within a twelvefold-symmetric tiling has an appeal.
It isn't possible using just squares and triangles to construct any finite shape with more than sixfold symmetry, and it is also true that an infinite square-triangle tiling would have only sixfold symmetry at most to infinity around any center. However, most recursive tilings share a property with the Penrose tiling, that one can find any finite number of generations of the recurrence relation from any possible starting point in the tiling. Thus, as long as the recurrence leads to the same sixfold-symmetric subregion in both one orientation and the one that is rotated 90 degrees from it, and these regions lead to everything else in the tiling, looking at any finite part of the tiling, one could not tell which of the two orientations of a sixfold-symmetric seed it came from; this is a valid kind of twelvefold symmetry for an aperiodic tiling.
We could create a sixfold-symmetric tiling of this type from the one with more dodecagons given above by this rule: all neutral dodecagons are instead treated as oriented dodecagons sharing the orientation of their most recent dodecagonal parent, and starting from a dodecagon so that all parts of the tiling have a dodecagonal parent at least in the first generation. Then a square-triangle tiling could be created by replacing all oriented dodecagons by orientations of the dodecagon constructed by surrounding six triangles with alternating squares and triangles, since eliminating the neutral dodecagon also eliminates the rhomb.
One change in the rule would be required, though; the recurrence from one orientation of the dodecagon would have to include both possible orientations of the dodecagon.
This is an example of the type of recursion rule described,

and the central part of a tiling it could generate would look just like a conventional tiling with p6m symmetry,
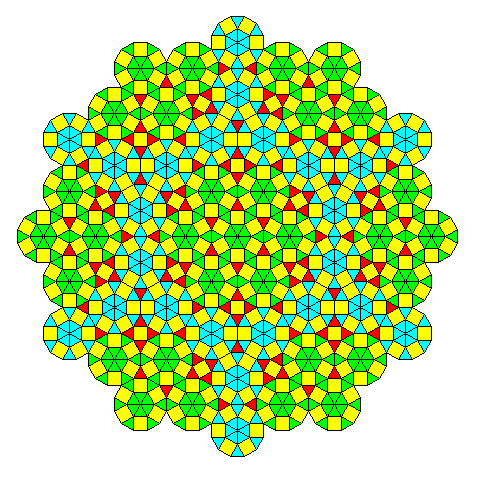
shown here with the triangles in the areas derived from dodecagons distinguished by color to make the symmetries more apparent, but if the tiling were continued further, its aperiodic nature would become apparent. The particular recursion rule chosen, with dodecagons of the rotated orientation only on the overlapping border, was chosen so that it would generate the tiling in this diagram, which matches the one in the paper by Baake, Grimm, and Moody cited above; however, that does not mean it is the same tiling, as the tiling that they were illustrating likely used a recursion rule differing from the one proposed here in at least a few minor respects. It may have even differed in its fundamental structure, by not being a transformation of a recurrence relation expressed in terms of dodecagons.
Examining the diagram suggests a recurrence like this, if one from the triangles and squares directly is used:
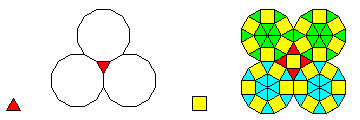
Since the squares are all connected to each other by one corner, there may be a way to uniquely determine their orientations. As for the triangles, a triangle might have dodecagons in two orientations if squares adjoining all its vertices force this, but if a triangle only has two vertices adjoining a square, then, at least in the area seen in the diagram, it can have three dodecagons of the same type, which, if a rule, would also influence how the squares can be oriented.
Using just the original recurrences for the square and triangle, and then filling in the dodecagons with the two possible orientations of the square-triangle filling at random gives the random Stampfli tiling.
However, since the twelvefold symmetry of a square-triangle tiling is of such a subtle nature, if it were desired to use the tiling shown earlier from the Topkapi scroll as source material for a twelvefold symmetric tiling, it would probably be better to make the twelvefold symmetry obvious. This would mean adding a rhomb to the square and triangle used in that motif:
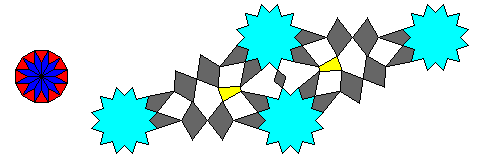
Therefore, the second modified dodecagonal tiling, which eliminates the rhomb completely, and can be used to make a square-triangle tiling, would not be used. In addition, since the rhombs are not as attractive as the square and the triangle, the basis of the tiling using this new shape, instead of being the initial dodecagonal tiling, would be the modified version of the initial tiling that reduces, but does not completely eliminate, the use of the rhomb piece, that is, the first modified tiling.
In this way, most of the dodecagons would not be neutral dodecagons, which would need to be decomposed to the twelvefold symmetric shape shown made up of twelve triangles and twelve rhombs. This allows the dodecagons that are not neutral to be decomposed to the same square-triangle oriented shapes in the way indicated in the second modified tiling.
Since the neutral dodecagon in the center of the recurrence for the neutral dodecagon is surrounded by triangles whose orientations cancel out, one could modify the first modified tiling by adopting the rule shown below
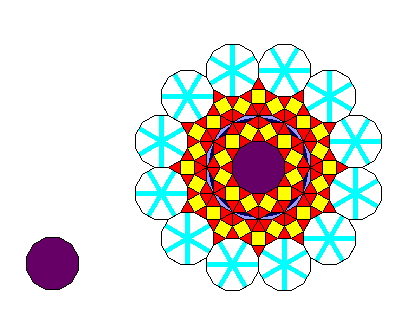
for the recurrence of the neutral dodecagon. We could also give the orientations of the border dodecagons in this recurrence for the neutral dodecagon the lowest priority, instead of the highest, as will remain applied to the overlapping dodecagons in the recurrences from the oriented dodecagons. Of course, this means that while twelvefold symmetry remains, reflection symmetry along the twelve axes is surrendered.
Another modification we could make, since a neutral dodecagon has twelve rhombs in it, is that when the dodecagon in the obtuse corner of a rhomb after being expanded by the recurrence relation, would become a neutral dodecagon, we would instead go to the recurrence for a rhomb in the unmodified tiling, since that has fewer rhombs.
This tiling would create a result part of which would look like this, before replacing the rhombs, squares, and triangles by elements of the Topkapi scroll pattern:

The alternate colors used for triangles in this image, intended to make the structure of the tiling clearer, reduce the symmetry from twelvefold spiral symmetry to only sixfold, but they are not part of the tiling itself.