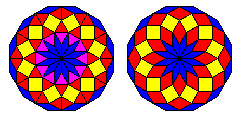
In the initial page on dodecagonal tilings, it was noted that square-triangle tilings with dodecagonal symmetry came up in the study of quasicrystals.
Another group of tilings, other than the Socolar tiling, appears in the study of quasicrystals; these tilings consist of thin rhombs, thick rhombs, and squares. These are the kinds of tilings that computer programs using the dualization method due to de Bruijn will generate. Such tilings can have full dodecagonal symmetry; one kind of center such a tiling can have is compared to the center of one of the tilings produced by recurrence relations:

If one breaks up the thick rhombs into two equilateral triangles, one of these tilings will correspond to the 12-star tiling of Stampfli.
I have been able to obtain from one source the following incomplete recurrence relation for the 12-star tiling:
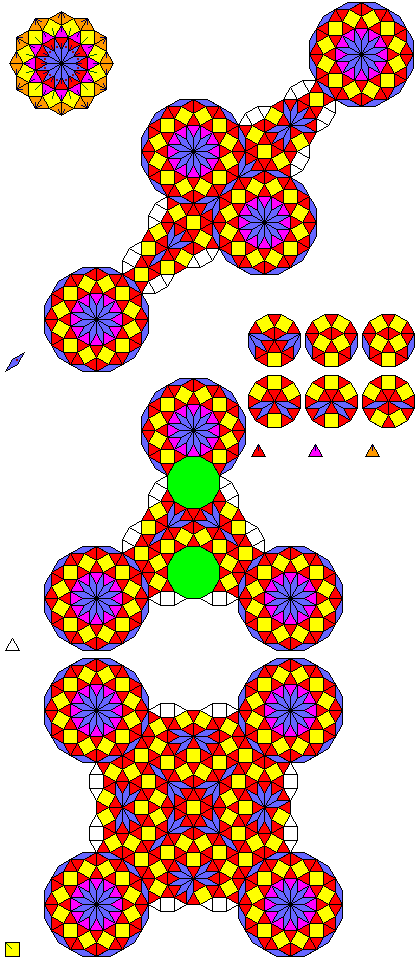
As some triangles occur in groups of three, however, it does not appear to be derived from a pure rhomb tiling. Note that while some overlapping tiles are shown uncolored, the rosettes surrounding each of the vertices of the tiling from which the recurrence is performed are shown completely filled in, even though they will overlap.
Note that three variants of the triangle are shown in the diagram; the triangle has two unbroken dodecagons, and above the symbol for each type of triangle, what replaces the two dodecagons is shown.
This recurrence relation was termed a super-inflation. There is a property which falls short of a recurrence at a smaller scale: if one rotates a 12-star tiling by 15 degrees and expands it by a factor of sqrt(2 + sqrt(3)), and superimposes it on its unchanged version, at least starting from a suitable point such as the center of complete 12-fold symmetry, the vertices of the enlarged tiling will all coincide with vertices of the original tiling. However, triangles will break down into several different possible combinations of smaller tiles.
What is shown above also falls short of a recurrence relation. Although only one kind of rhomb is shown, the next layer in the inflation of the rosette will have to include a rhomb whose two ends are symmetric, and it may be that there are other kinds of squares and triangles in addition to those shown.
The partial rosette in the upper left corner of the diagram shows, from the component types described in the diagram, the overall plan of the central part of the 12-star tiling, as much of it as I could determine from an illustration in the same paper by Hans-Ude Nissen as was noted on the previous page for its observation concerning the Socolar tiling.
It was noted, in the original paper by Stampfli in Helvetica Physica Acta which described this tiling that it can be constructed as the dual of a pair of superimposed hexagonal tilings, rotated by 30 (or 90) degrees relative to each other; the Socolar butterfly tiling is similarly the dual of a pair of superimposed triangular tilings.
An analogous relationship exists between the Penrose rhomb tiling and the anti-Penrose tiling.
Such an overlapping grid of hexagons looks like this:
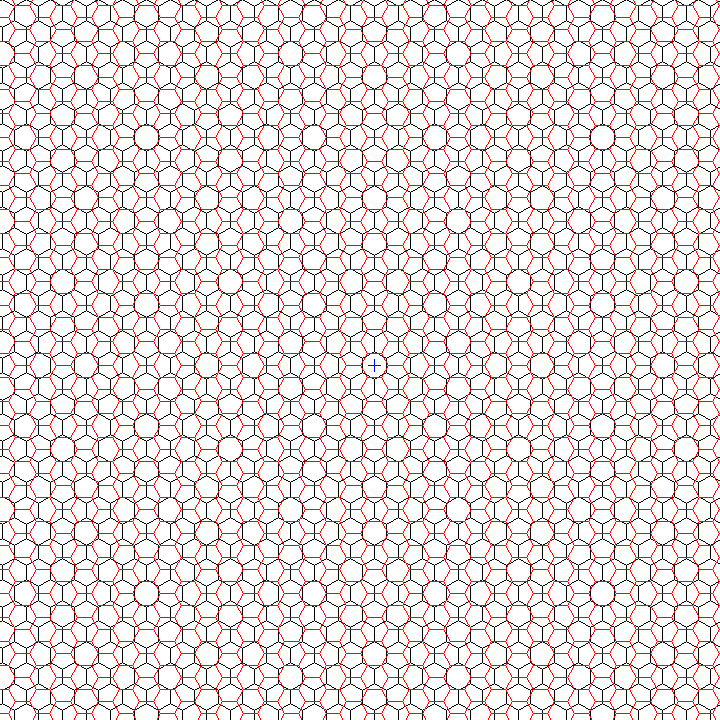
In order to draw this image to the required degree of accuracy, I began with a hexagon which was 24 pixels wide and 28 pixels high, and, since the exact value for the height should be 27.7128129... pixels, I shortened two rows of hexagons by one pixel out of every seven rows. One would have to do this thirteen times before another adjustment became necessary. Yes, this wasn't drawn by a computer program, although with copy and paste, I did not draw more than a very few hexagons by hand...
A diagram such as this also suggests that it is to be regretted that the study of Moiré patterns did not lead to the discovery of quasiperiodicity before it was discovered by other means.
In any event, one must proceed from this pattern to obtain the 12-star tiling by dualisation, and so one is not quite using an acceptance domain to take a slice through (in this case) 6-space.
Another important tiling, containing squares, triangles, and a few thin rhombs, is known as the ship tiling.

Here, it is noted that the rosette shape can have its circular part formed by six dodecagons containing two rhombs, and so the entire tiling is built up from that particular kind of dodecagon in various orientations, plus either single triangles or squares surrounded by four triangles to join the dodecagons.