This tiling comes in several closely related forms. One is the original Socolar tiling, also known as the butterfly tiling, with squares, hexagons, and thin rhombs. (A trivial variation on this one, just changing the shape of the pieces, is known as the plate tiling. But this trivial change is still of interest in a way, as it makes some of the symmetries of the tiling more visible.) Just as the Penrose tiling has several related forms, this tiling has two other isomorphic forms with different tiles; one is the shield tiling, and the other the wheel tiling which involves only two shapes of piece.
The substitution rules of the Socolar tiling, here shown through two generations, are very similar to those of the Ammann-Beenker tiling in appearance:
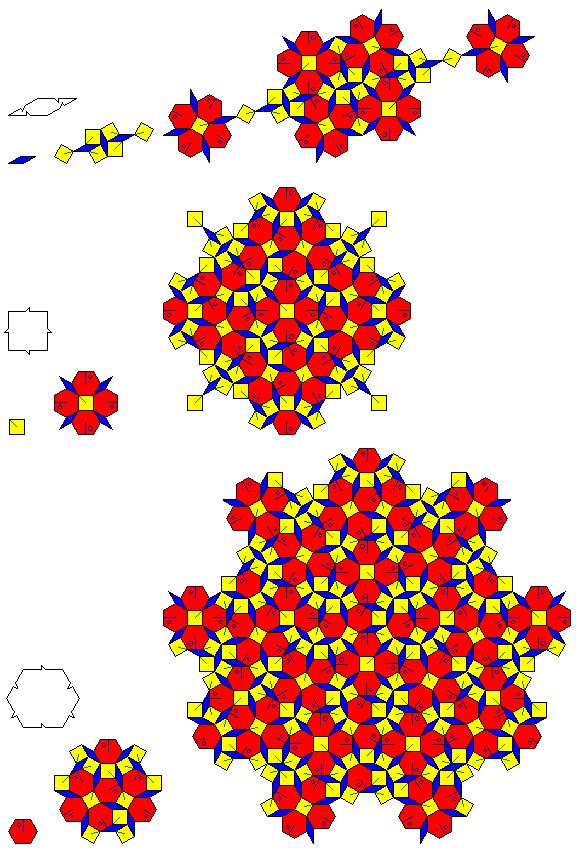
but, as can be seen from the diagram above, they are more complicated.
In addition to showing one generation of the recurrence relation, the matching rules are also shown. The notches on the tiles indicate which edges can meet, and in which directions; as well, not only is it not possible, as indicated by the notches, for two squares or two rhombs to touch, it is also not allowed for two hexagons to touch (although that is a derivable long-range property, since the notches do not allow three hexagons, or two adjoining hexagons plus a rhomb and a square, to meet around a vertex).
Note that while the diamond has all the symmetry its shape implies, the square has a preferred direction, and is bilaterally symmetric perpendicular to that direction, and the hexagon is not symmetric. As well, both the form of the hexagon depicted in the bottom part of the diagram and its mirror reflection are used in the tiling, as can be seen from the fact that its mirror reflection is called for in the recurrence relation shown.
It may also be noted that the recurrence relation does preserve all the symmetry each piece is claimed to have, or, rather, all the symmetry each piece is left with after the matching rules are considered.
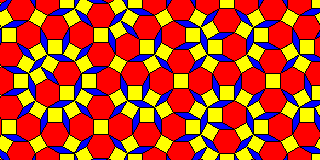
And here is what a part of a Socolar tiling looks like:

As with the Ammann-Beenker tiling, there are obvious linear features where a number of rhombs are pointing in the same direction, which suggest that they are, or are associated with, the Ammann bars of this tiling.
Also, the occurrences of this symmetrical cluster in its various orientations:
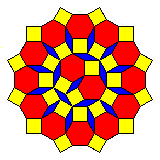
do, as the diagram above can only suggest due to its limited extent, form the vertices of a square-triangle tiling, as was noted in a paper by Hans-Ude Nissen in Proceedings of the 5th International Conference of Quasicrystals that discussed this tiling and several related ones.
The distances between Ammann bars in the Penrose tiling are in the golden ratio, (1 + sqrt(5))/2. In this tiling, the distances between rows of rhombs are in the ratio of (4 cos(15°) + sqrt(2))/2 cos(15°), and since the cosine of 30 degrees is sqrt(3)/2, it is possible to convert the cosine of 15 degrees to radicals as well;
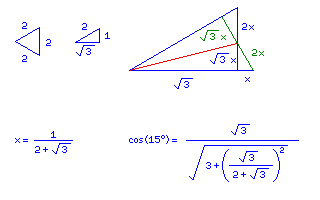
As noted, there are other related forms of the Socolar tiling. Here is a smaller area of the tiling:
And here is the corresponding area of the shield version of the tiling:

and here is a diagram showing the relationship between the two:

As for the plate tiling, as the relationship is so simple and direct, only a small diagram is required:
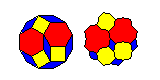
One reason this form of the tiling has significance is that the shape of the pieces helps to illustrate one aspect of the matching rules.
On the other hand, the wheel tiling looks very different, so much so that at first one might wonder if there is any relationship at all:

But when the outline for the wheel tiling is overlaid on the original Socolar tiling, the relationship becomes obvious:
