There are also tilings with octagonal symmetry that are like the Penrose tiling. One of them is the Ammann-Beenker tiling. This tiling uses two pieces, a square and a diamond. It can be formed either by recursion or by matching rules.
Two generations of the recurrence relation for the Ammann-Beenker tiling are shown below:
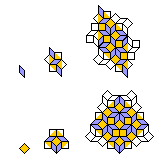
Since the recurrence for the square reduces its symmetry to bilateral symmetry, of course, this recurrence does not tell the whole story; the orientation of the expanded version of a square would have to be inferred from surrounding rhombs.
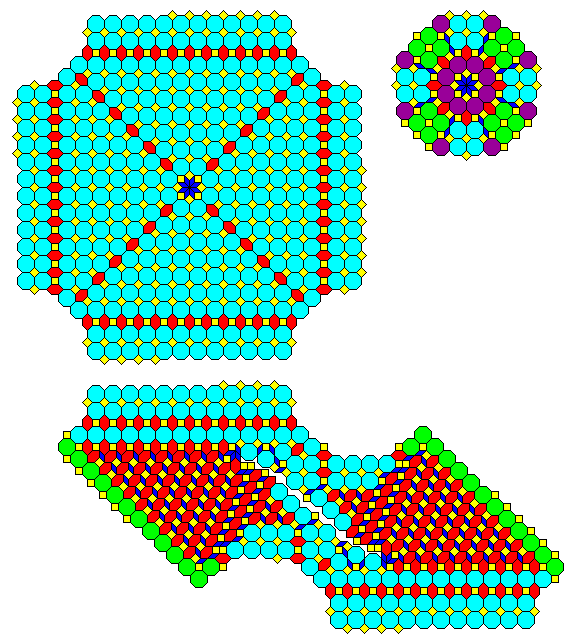
And here is a small portion of this tiling:

Note obvious linear details in this image. From symmetry, it would appear that where long rows of rhombs are all pointing in the same direction, the corresponding Ammann bars must run down the middle of the rhomb, but I have seen no reference for the alignment of Ammann bars relative to the other obvious linear features, where one sees a line of rhombs with directions pointing to one or the other side of the line with a deviation of 22 1/2 degrees next to a line of squares. Nor do I know where the Ammann bars of the Socolar tiling are located.
As the matching rules for those two pieces are somewhat complicated, the diagram below, which illustrates them, does so by means of adding a third piece, an octagon, which enforces the matching rules for the corners of the diamonds and squares.
Note that although these component tiles are drawn similarly to those on the previous page, the outer row of octagons on adjacent pieces does not overlap; instead, the squares nestled into the indentations between adjacent octagons are used to indicate matching rules.
Unfortunately, taking a little bite out of the obtuse corners of the diamond makes it impossible to draw from component pieces. Using conventional diamonds and squares, as shown on the previous page, to make an Ammann-Beenker tiling is, of course, entirely possible, and so recursion from one into a few Keplerian layers can be done, one just has to observe the matching rules through some other device than explicit shape fitting. This would lead to results like this:

Note also the symmetrical version of the octagon with an even number of octagons on its sides; this could be used as an alternative in the recursion relations on the previous page.