On another page about tilings, I illustrate a conventional tiling from the Islamic world whose unit cell is the thick rhomb shown in the illustration below:

Added in this illustration is a thin rhomb that can be combined with it to permit that motif to be extended to the Penrose tiling, or to binary tilings such as the Mikulla-Roth tiling.
The illustration below suggests how these rhombs may be used:

Incidentally, using a simpler tiling with the same basic geometry as the tiling on which this is based, Craig Kaplan used Quasitiler to modify it to a version which could be used for the Penrose tiling in the same way.
Since this page was written, a paper by Peter J. Lu was published in the February 23, 2007 issue of Science concerning the discovery of patterns in Islamic art which appear to embody genuine quasicrystalline pentagonal symmetry. This was inspired by patterns including decagonal figures one of the researchers had seen while in Uzbekistan; while it was well known that decagonal and pentagonal elements appeared in Islamic tilings, to the best of our former knowledge, true overall pentagonal symmetry had not been reached, even by the Keplerian technique of self-similarity.
In a royal palace in Fez, Morocco, there is a design with pentagonal symmetry of the Dürer type that I have seen pictured.
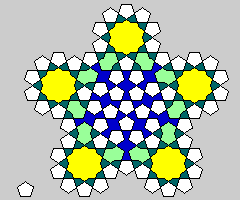
The recurrence relation for the pattern found on the Darb-e-Imam shrine and mosque in Iran which appears to make the definitive case for true quasicrystalline patterns in Islamic art long predating the modern discovery of such patterns by Roger Penrose appears to be something such as the following:
The recurrences involve the yellow star shape at the vertices of the component shapes, and so one should draw a line through the centers of the yellow stars at the vertices to determine the exact bounds of the recurrence. Such lines are part of the actual design as it appears on the mosque. It should also be noted that while each individual type of piece has been given its own color in the diagram above for clarity, in the design as seen, the light green overlapping pentagon piece is also white, like the pentagon, and the kite, shown here in dark blue-green, and the bow-tie, shown here in blue, are both black.
The recurrence for the pentagon found in the tiling as it appears on the Darb-e-Imam mosque is asymmetric.
No recurrence for the blue bow-tie piece is exhibited in the portions of the tiling that appear on the Darb-e-Imam mosque. One can be conjectured, but in a recurrence for that shape, it is necessary to replace four of the yellow stars at the vertices by component shapes, as they overlap; as long as these replacements take precedence over stars in adjoining shapes, is is still possible to fit the pieces together and extend the recurrence indefinitely.
However, the fact that the blue bow-tie shape is not exhibited as part of the second-level recurrence is actually surprising, since, as can be seen in the diagram above, the bow tie shape makes its appearance quickly.
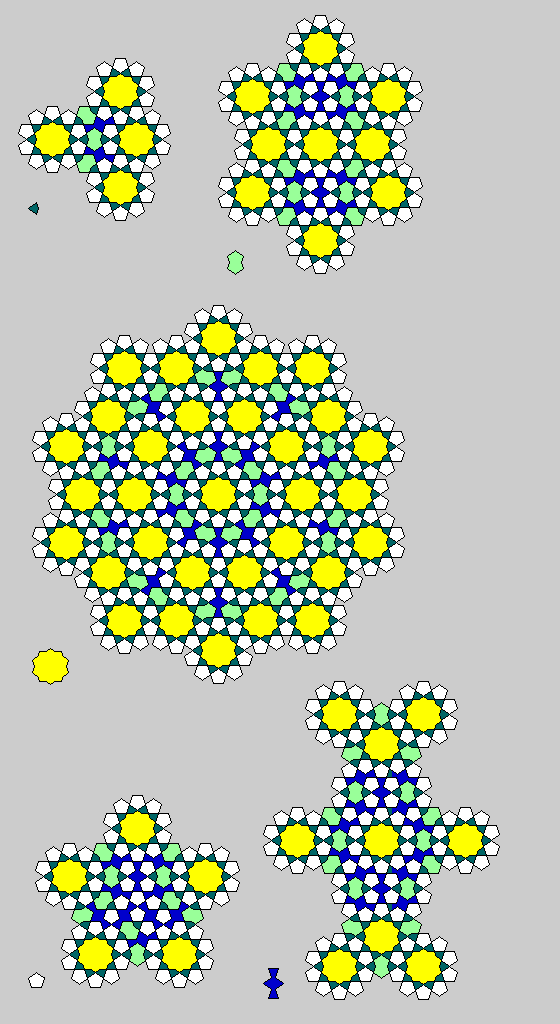
The upper level pattern for the design on the Darb-e-Imam mosque, from the parts available, appears to be the following:

which is a conventional symmetric pattern with a unit rhomb, belonging to the symmetry group cmm. However, this doesn't vitiate the importance of this pattern, since, even if recurrence was not used to make a pattern with overall pentagonal symmetry, the principle of recurrence, and its potential to make such a pattern, are still made obvious from the design. It certainly is possible to compose the various large-scale pieces used in the design from small-scale pieces of the same shape as a decorative embellishment without making the conceptual leap to the notion of infinite recursion, but even if we have as yet no proof that this leap was made before modern times, I suspect it would have had to have occurred, over the centuries, at least to some of the children who passed by this edifice.
Figure 3 of Peter Lu's original paper, based on an illustration of a somewhat small portion of this pattern in the corner of a doorway, illustrates this, and the same upper-level pattern was visible to me in a photograph of a larger portion of this pattern in an archway.
The illustration below shows about how much of the pattern can actually be inferred from that photograph (of course, one can also safely assume that the four star shapes, half of each of which is visible, would be complete): note that the lines showing the recurrence relation are actually present in the original design, one of the things that contributes to its significance:

The recurrence for the pentagon actually seen is asymmetric. At first, I thought that while it might seem as if pentagon-shaped areas on the sides of the parent pentagon could be rotated so as to eliminate the asymmetry, it would be impossible to do so, as for the pieces to join properly, the green shape formed from overlapping paired pentagons must be between the two stars for each long side. But because the pattern is so constructed that light pieces always touch only dark pieces and vice versa, the case of the pentagon can be made to override the green shapes shown for other shapes.