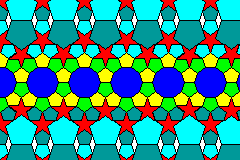
Inspired by revisiting the pentagonal tiling on the previous page to look again at making a tiling with pieces having pentagonal symmetry only, even if the tiling, like Dürer's tiling, does not have overall pentagonal symmetry, I only get a little way before failing,

as Kepler did when he attempted the same thing.
Another solution to eliminating the diamond pieces in addition to the hat pieces might be found by adding some new types of pentagonally-symmetric pieces based on combinations that sometimes arise which require diamond or hat pieces but which are themselves pentagonally-symmetric:
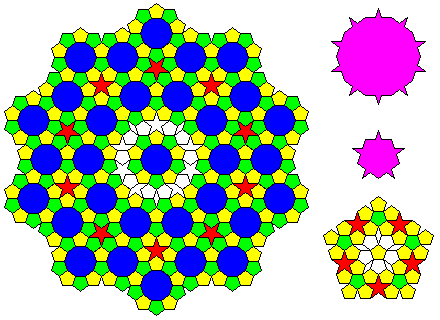
Of course, one certainly can tile the plane only with pentagonally-symmetric pieces, or even only with pentagons, if one is allowed to go on adding one new piece after another, since that is related to the principle behind Dodecafoam. Following that route, one might obtain something like the following:

But it certainly could happen that one would eventually reach the point where a finite set of pentagonally-symmetric shapes could serve as the starting point for ever larger pentagons, stars, decagons, and other required pieces.
The diagram above may look like a tesselation, but if one goes further, it will break down, requiring a new, larger type of piece with fivefold symmetry to be added.
That no tiling is yet known that achieves reliance on only pieces with fivefold symmetry, and which also uses a finite set of tiles, is noted in a 1982 paper in the American Mathematical Monthly by Danzer, Grünbaum, and Shephard, cited in the Ph.D. thesis of Craig S. Kaplan, which is available on the Internet.