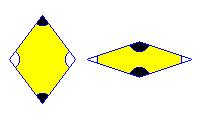
The matching rules for the thick and thin rhombs are different in kind from those for the kites and darts in the two basic two-tile versions of the Penrose tiling we have seen on the previous page:
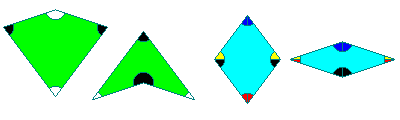
The matching rules for the kites and darts are based on matching colorings for the points, while those for the thick and thin rhombs are based on matching directions for the sides.
If one were to take the thick and thin rhombs, and give them matching rules similar to those used for the kites and darts, as it happens, another interesting tiling with overall pentagonal symmetry can result, called the binary tiling.
The matching rules for this tiling are:
The recurrence relationship for this tiling is particularly challenging to grasp, and thus the diagram below depicts four levels of that relationship:
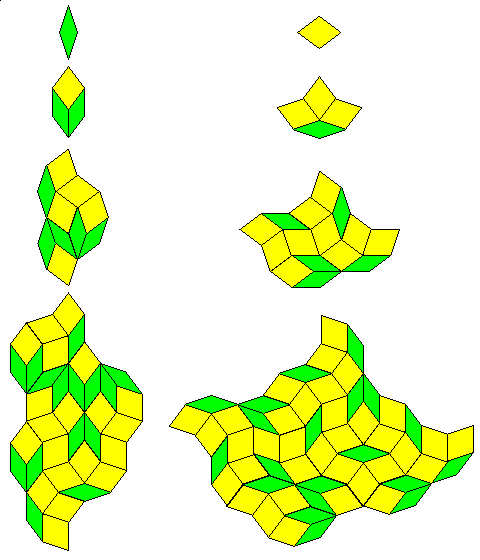
Note that the boundary of the area under the recurrence, if the recurrence is allowed to repeat infinitely, is a fractal curve.
The matching rules for the binary tiling given above, however, do not enforce the recurrence relation given above. In fact, they are not enough even to enforce an aperiodic tiling. The larger thick and thin rhombs below:

can be constructed from thick and thin rhombs obeying the binary tiling matching rules. These larger thick and thin rhombs, however, do not need to observe any matching rules; the thick rhomb alone can be used to tile space periodically, for example:

and together they can, of course, be used to make either the aperiodic binary tiling shown above, or a Penrose rhomb tiling, or a recursive tiling based on their own structure, or any other edge-aligned tiling made up only of thick and thin rhombs.
One can go further, and using the thin rhomb as a diamond piece, add a boat, a star, and a pentagon built from the thick and thin rhombs arranged in a binary tiling:
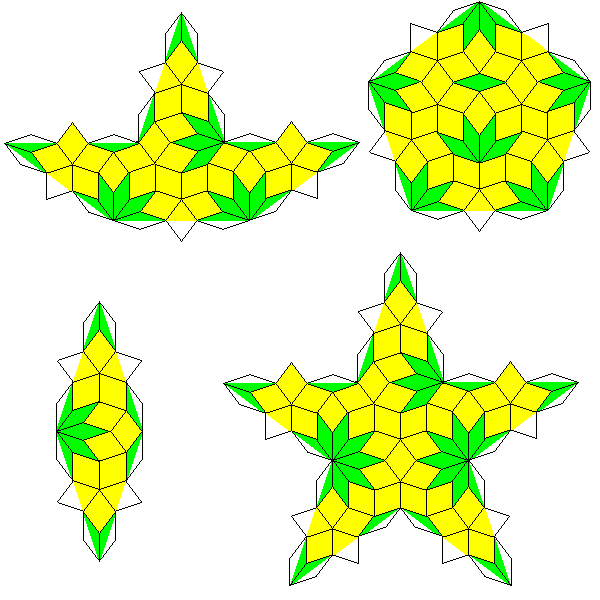
and these arrangements appear to occur in one tiling, the Mikulla-Roth tiling, of interest to researchers studying quasicrystals.
The actual formation of the Mikulla-Roth tiling, however, does not involve those pieces. If one takes a Penrose rhomb tiling, and divides the thin rhombs into two acute isosceles triangles by drawing a line between the two points that are close together, and divides the thick rhombs into two obtuse isosceles triangles by drawing a line between the two points that are far apart, one obtains the Robinson triangle tiling. The recurrence relation for the Robinson triangle tiling is shown on the left side of the diagram below:
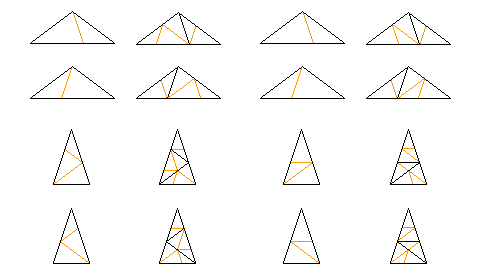
The black lines indicate the triangles of the current generation; the orange lines indicate the boundaries of the triangles of the next generation, for the purpose of showing the orientation of the triangles of the current generation. The right side of the diagram shows a similar recurrence relation, but for the Tübingen triangle tiling. The Mikulla-Roth binary tiling is obtained from the Tübingen triangle tiling by treating all the triangle vertices as "large" atoms, that is, the sharp vertices of the thin rhombs and the blunt vertices of the thick rhombs, shown by white circles in the matching rules above, and by placing a "small" atom, or a black circle, in the middle of each acute isosceles triangle only.
However, we will see below a more fundamental relationship between tilings involving pentagons, diamonds, boats and stars and binary tilings. The reason that the family of binary tilings in general is of interest in studies of quasicrystals is because the two kinds of corners can be thought of as corresponding to two atomic species in a crystal, the ones indicated by white circles, at the acute ends of the thin rhomb, corresponding to the form of atom requiring more space.

Going back to tilings involving actual pentagons, such tilings, whether they are the original Penrose tiling, or other tilings, such as a Keplerian tiling, as long as they use only the diamond, boat, and star in addition to pentagons, and do not allow those pieces to touch, can be converted to another form, known as the HBS, or Hexagon-Boat-Star, tiling, an example of which is shown at left.

Even the Goethe tiling, illustrated at the beginning of this section, can be reduced to a tiling of the HBS type, but using only the hexagon piece. It should also be noted that the boat piece can also tesselate space, and thus there is a pentagonal tiling which uses only the boat piece, with no diamonds (or stars) at all, as depicted on the right. Since the diamond piece can be eliminated from a pentagonal tesselation (earlier, we managed to eliminate the boat, but not the diamond, by using pieces with five-fold symmetry), one wonders if the goal of a tiling based on pieces with pentagonal symmetry only might be attainable. And aperiodicity is not guaranteed, in the absence of additional matching rules, even if all three kinds of pieces are used; thus, the periodic background to that page, made from a repeated rectangular section of a Keplerian tiling, can be made into an HBS tiling.
The importance of the HBS tiling is not simply that it provides a clear formal definition of the type of pentagonal tiling with which this section began, as long as extra pieces such as the double-sized pentagon and the decagon are excluded. Instead, the HBS tiling is significant because of the fact that there is a relation between HBS tilings and binary tilings.
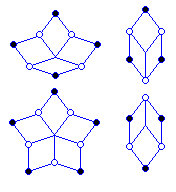
The diagram at left shows that the boat, star, and hexagon shapes can be built out of the two rhombs following the binary tiling matching rules. Note that the hexagon can be aligned so as to reverse the sequence of white and black vertices on its edges.
But the other two pieces cannot. As it happens, however, the way that boat and star pieces appear in a pentagonal tiling that can be made into an HBS tiling means that this is no problem.
Also, note that in all three pieces, the edges of the rhombs that don't participate in the boundary of the piece all join points on the boundary to one point within the piece. This suggests that those edges might form the boundaries of shapes which tile the plane in a tiling that is the dual of a given HBS tiling, in the same sense, or nearly the same sense, that the octahedron is the dual of the cube, or the dodecahedron is the dual of the icosahedron.
What is even more astounding, however, is that this other tiling will also be an HBS tiling in its own right.
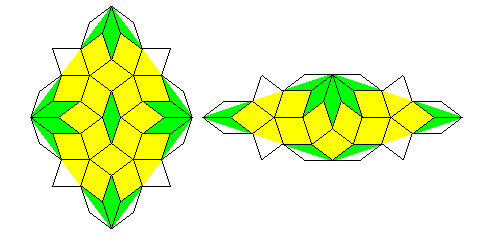
One example is shown here, with the version of the binary tiling that began this page:
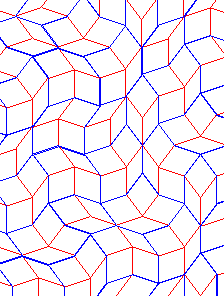
This tiling involves only hexagons and boats, however, with the star not even putting in an appearance.
If you look at the relationship between the original Penrose tiling and the Penrose rhomb tiling, at first glance, it strongly resembles what we have been discussing here. The rhomb boundaries do include sides which form an HBS boat around each boat of the original Penrose tiling, an HBS star around each star of the original Penrose tiling, and an HBS hexagon around each diamond of the original Penrose tiling. But the Penrose tiling is not a binary tiling. And the left-over rhomb boundaries, therefore, do not themselves form the boundaries of another HBS tiling. The difference is that the rhombs within each hexagon are reversed.