I was inspired to begin this page by current events. Some fans of a popular collectible card game were chagrined by some changes to its rules which were intended to simplify them. Thus, I thought now was the time, when people were quitting one very complicated game in search of another, to present one of history's most complicated board games, as it might serve as a potential alternative. At least, if one's tongue is firmly in cheek.
The main source for the information on this page about Rithmomachy is the copy of William Fulke's account of the game on this site, although some information has been obtained from a few other pages as well.
A series of numbers increasing by constant steps is said to be in arithmetic progression:
1, 2, 3, 4, 5, 6... 2, 4, 6, 8, 10, 12... 1, 3, 5, 7, 9, 11... 2, 5, 8, 11, 14, 17... 11, 21, 31, 41, 51...
A series of numbers increasing by a constant factor, thus exhibiting exponential growth, can also be referred to as being in geometric progression:
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 65536, 131072... 1, 3, 9, 27, 81, 243, 729, 2187... 1, 5, 25, 125, 625, 3125, 15625... 8, 12, 18, 27 27, 36, 48, 64
The last two examples show that if one chooses the right starting point, one can get several integer values in a row even if one uses a multiplicative factor such as 3/2 or 4/3.
The terms "arithmetic progression" and "geometric progression" are due to Anicius Manlius Severinus Boëthius. He wrote a book on arithmetic which was very popular during the mediæval period, and he also wrote the book The Consolations of Philosophy while he was imprisoned, awaiting execution at the order of the emperor Theodoric after having defended the senator Albinus against accusations of treason. October 23rd, the day of the year on which Hungary was invaded in 1956, is St. Severinus Boëthius' Day.
Boëthius lived during the late fifth and early sixth centuries, approximately from 480 AD to 525 AD. In his work De Institutione Arithmetica (billed as in two books, this being common with older books; thus, Trithemius Polygraphia is noted as being in six books) in addition to the arithmetic progression and the geometric progression, he defined the harmonic progression. Some examples of series of numbers in harmonic progression are given below:
2, 3, 6 3, 4, 6, 12 10, 12, 15, 20, 30, 60 21, 24, 28 36, 40, 45 55, 60, 66
In the series 10, 12, 15, 20, 30, 60, the differences between successive terms in the series are 2, 3, 5, 10, and 30. For any three consecutive numbers in the series, the ratio between the first and third numbers is the same as the ratio between the differences between the first and second numbers and between the second and third numbers.
Thus, for the numbers 10, 12, and 15, 15 is to 10 as 3 is to 2.
For the numbers 20, 30, and 60, 60 is to 20 as 30 is to 10.
Note that if one multiplies all the numbers in a series of numbers in harmonic progression by the same amount, they remain in harmonic progression, as is also true for the geometric and arithmetic progressions. Adding the same number to each member of the series, on the other hand, disturbs the progression, except in the case of numbers in arithmetic progression.
There is, though, a simple key to harmonic progression. Let us take, for example, the harmonic series 10, 12, 15, 20, 30, 60, and divide 60 by each number in the series in turn. The results are 6, 5, 4, 3, 2, and 1. Or, for the series 21, 24, and 28, divide 168 by each number in turn; then, the results will be 8, 7, and 6. So a harmonic series is one in which the reciprocals of the numbers in it are in arithmetic progression.
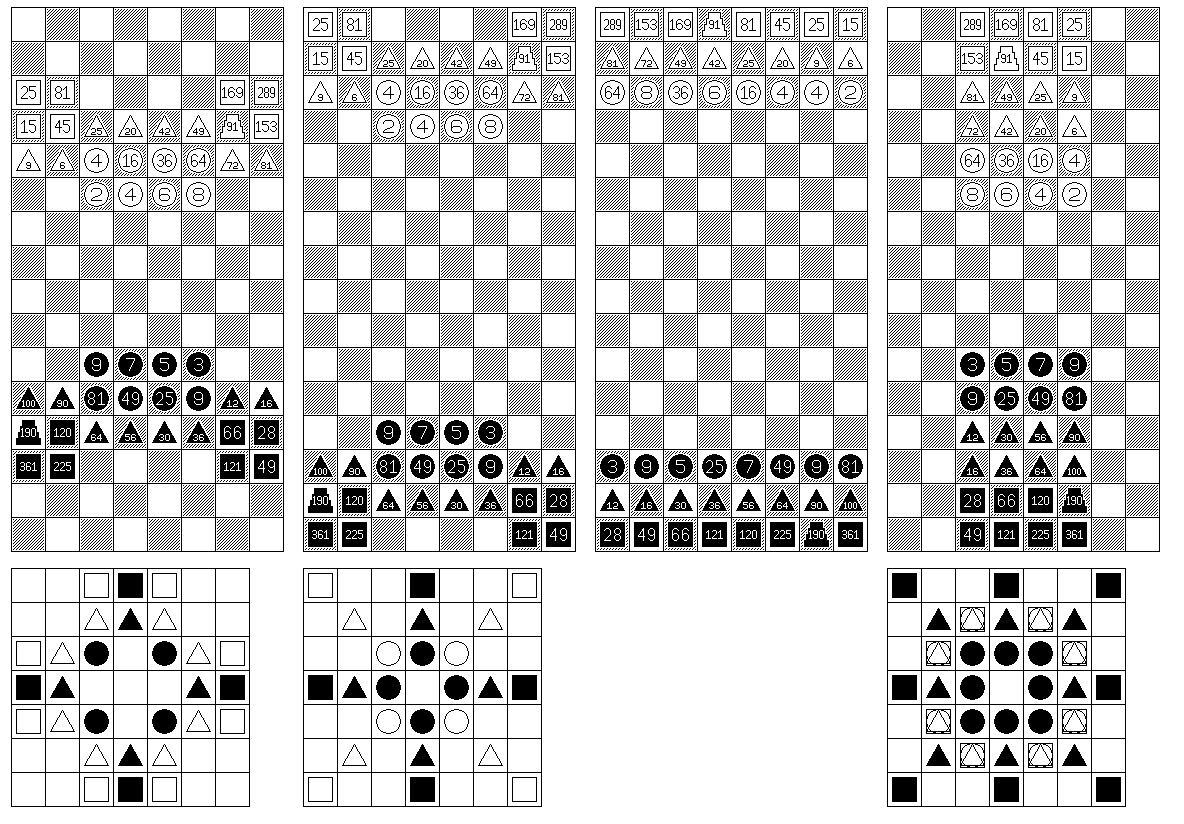
In the next section, a diagram of the initial arrangements of the board and men for Rithmomachy is shown. The fourth arrangement pictured is the one which most clearly positions the pieces in accordance with the way that the numbers on them were derived.
2 4 6 8 3 5 7 9 n 4 16 36 64 9 25 49 81 n*n multiplex n* 6 20 42 72 12 30 56 90 n*(n+1) superparticular ((n+1)/n)* 9 25 49 81 16 36 64 100 (n+1)*(n+1) superparticular ((n+1)/n)* 15 45 91 153 28 66 120 190 (2n+1)*(n+1) superpartient ((2n+1)/(n+1))* 25 81 169 289 49 121 225 361 (2n+1)*(2n+1) superpartient ((2n+1)/(n+1))*
The terms multiplex, superparticular, and superpartient denote types of ratios, and refer to the ratio between the numbers in each row and the row preceding it.
The numbers in the second row are all integer multiples of the numbers in the preceding row, so the ratios between them and those numbers are multiplex ratios.
The next two rows are multiplied by a ratio which, in lowest terms, consists of two numbers which differ by 1, such as 4/3 or 9/8. Such ratios are termed superparticular ratios.
The final two rows involve the ratio (2n+1)/(n+1), which is guaranteed to reduce in lowest terms to a fraction with a difference greater than 1 between its numerator and denominator, and this ratio is called a superpartient ratio.
The game of Rithmomachia (Arithmomachy, Rithmomachy or Rythmomachy) makes use of these three kinds of progression.
Several different forms of the game were played. The diagram below shows four possible starting arrangements for the pieces:

Two of the pieces shown, the white piece with the value 91, and the black piece with the value 190, are pyramids, which are stacks of pieces.
I show the black pieces at the bottom, because black moves first, the numbers on the white pieces giving white an advantage because they enter into combinations somewhat more easily. According to at least one source, because the board is so much longer than wide, however, and because mediæval players usually used a board with relatively large squares, similar to those of a tournament chessboard or checkerboard, at least about 2 inches or 5 centimeters on a side, instead of sitting behind their own rows of pieces, as is done with chess and checkers, players usually sat on the two sides of the board so that they could reach the whole board better.
Below three of the starting arrangements shown, the moves of the pieces for the version of the game played with that starting arrangement are shown, as they were given in the description of Rithmomachy by William Fulke in 1563, which was translated from one by Claude de Boissière. The second and third arrangements illustrated are two different arrangements both used for playing by a second set of rules, and thus one illustration of movement is placed below the illustration of the second starting arrangement.
In each of the diagrams of how the pieces move, pieces are considered to start from the center of the 7 by 7 square used to illustrate movement.
The solid black pieces of each shape show the normal move of the piece of that type. These moves are made in a straight line, to the full number of spaces shown, and cannot involve jumping over any intervening pieces.
In the first version of the game, the white triangles and squares show the flying move of these two pieces. The flying move may be made at any time; unlike the regular move, there is no concern with intervening pieces. This move may not be used to make a replacement capture (including captures where actual replacement does not take place, but the piece being captured is on a square to which a capturing piece may move), but it may be used to make a custodian capture (which requires the piece to be surrounded on four sides).
In the second version of the game, to which the second and third starting arrangements are applicable, all three types of pieces normally move orthogonally only, but the game is also sometimes played with the agreed-upon rule that they may move diagonally as well, and thus a white circle, triangle, and square show the moves for this alternate form of the game.
In the third version of the game, to which the fourth starting arrangement illustrated is applicable, the symbols consisting of a white circle, triangle, and square superimosed together show a move available to all these pieces, but not to the pyramids, either to surround an enemy piece to capture it, or to escape from being surrounded.
Some accounts of the second version of the game simply state that Rounds, Triangles, and Squares are all allowed to move diagonally as well; in Fulke this move is noted for this version of the game as one that is sometimes agreed to by the players, as noted above. As well, also in Fulke, it is noted that in the third version of the game, it is sometimes agreed that the Triangles and Squares are allowed to jump over intervening pieces.
The first version of the game is also sometimes played on an 8 by 12 board, without the two empty rows of squares behind the pieces. It can also be played on an 8 by 9 board by moving the two arrays closer together, so that there is only one row of spaces between them; such a board was termed a practice board, as opposed to the tournament board on which the two arrays are in their normal positions.
The pieces are disks, triangles, or squares, and they may be marked with the same number on both sides, but in opposite colors, so that a captured piece can be re-entered on the capturing player's back rank as an additional piece.
The rules for this vary between the different forms of the game.
In the first form of the game, if a piece is captured, it is immediately entered, with the other color turned up, on the back rank of the player that captured it. This does not apply, however, to the pieces of which the Pyramid is composed, which are not re-entered on the board.
In the second form of the game, it is stated in Fulke that captured pieces are not re-entered on the board, but this would appear to make Victoria Excellentissima impossible for the player with the black pieces. Another account for the rules of the second form of the game allows the opponent's Pyramid, once it is fully captured, to be re-entered as a unit, but no other pieces may be re-entered on the board.
In the third form of the game, captured pieces are not re-entered on the board, but they are still described as having the same number in the opposite color on the other side. A captured piece may be counted as part of a winning combination, without having to be placed anywhere on the board. (It would seem that there is no real reason that it is necessary to provide the numbers in the opposite color on the other sides of the pieces to facilitate this.)
To permit all the greater victories to be won in the second form of the game, it seems that the rule in the third form, allowing captured pieces to count as part of a winning combination, would need to be applied in that form as well.
The rules for capturing an enemy piece are similar in the different versions of the game, but not identical.
Some captures involve a piece being captured when it is flanked or surrounded, while others involve a piece being captured when it is in a square to which one or more of its opponent's pieces can move, but in that latter case, the movement does not take place.
Since captures take place without involving movement, they take place in addition to movement. During a player's turn, a player may make all available captures twice, before moving a piece, and after moving a piece. Capturing is, however, optional, not compulsory. Thus, for a capture by addition, for example, if at the beginning of a turn two of one's men can move to a given square, and their sum equals the number on the opponent's man on that square, it is captured without either of one's men moving as part of the capture, but it is permitted, if desired, that one's move for that turn could be to move one of those two men (or, for that matter, another of one's men that could move to the square vacated) to the square from which the captured piece was removed. (This, at least, is how I interpret the description in Fulke of capture by addition in the first form of the game which appears to state that if a piece is liable to capture by addition before the capturing player has moved a piece, then the capturing player may optionally move one of the capturing pieces into the vacated space. It is noted also that capturing by addition normally works the same way in the third form of the game.)
The different methods of capturing, and the versions of the game to which they apply, are:
Multiple captures may take place in the same turn, all those for which the conditions are met.
The opponent's Pyramid must be taken as a precondition to winning the game, but taking the opponent's pyramid does not win the game by itself.
The Pyramid can be taken by siege (or oblivion). Individual layers of which it is composed can be taken by other methods which apply to the numbers on them.
In the second form of the game, if a layer of the Pyramid is captured that layer may be ransomed by giving up a piece with the same numerical value as that layer, if one has it, and, if not, by allowing the other player to take any one piece of yours that he chooses.
This is also true in the third form of the game, except that the bottom layer of the pyramid may not be redeemed in that fashion.
Some accounts of the second form of the game state that capturing the bottom layer of the pyramid is a method for capturing the pyramid as a whole; in that case, it would not be subject to being ransomed in the second form of the game as well.
Any one game of Rithmomachy can be won in only one way, but the way in which the game is to be won is chosen from several possible winning conditions by agreement between the players before the game begins.
Prior to winning by the agreed-upon method, it is also necessary to capture the opponent's pyramid before one can win in any of these cases.
The first version of the game was generally won only with the greater victories. The second version of the game could be played for either the greater victories or the lesser victories. The third version of the game was to be played only for either one of the two larger of the greater victories, Victoria Major and Victoria Excellentissima. However, unlike the case with capturing methods, since a victory condition is established by agreement, I will simply list the victory conditions below without associating them with particular versions of the game.
A greater victory involves placing three or four pieces in the opponent's area of the board which satisfy certain of the numerical progressions discussed at the beginning of this page. For the first version of the game, each player's area of the board consists of the first five ranks of the board (although Fulke notes that some players use the first six). This would seem to imply that the first three ranks of the board should apply ot the second version of the game, and the first six ranks should apply to the third version of the game.
When a piece is placed within the opponent's area to form part of a greater victory, this fact is to be announced, and then that piece is immune from capture.
The lesser victories are:
The greater victories are:
The descriptions given above for Victoria Major and Victoria Excellentissima, however, are oversimplified. Most of the possible winning combinations given in tables for that game exhibit geometric proportion with two pairs of numbers that are in the same ratio to each other, rather than by including three numbers in geometric progression.
As the rules do not say anything explicit about this, it might be that exhibiting harmonic proportion with two pairs of numbers whose reciprocals have a common difference, or exhibiting arithmetic proportion with two pairs of numbers with a common difference, is also allowed; this possibility, however, has not enabled me to account for some apparent typographical errors in the table given in Fulke. He gives thirty combinations; four of which appear invalid, but two of which yield a valid combination once a minor typographical error is corrected. The resulting 28 combinations made a list I have seen quoted in several places on the Web, apparently quoted from the work of Peter Mebben as it appears here, but since then, I have found that this location gives a 29th combination which corresponds to one of the other combinations in Fulke.
As the number of possible combinations that can win with Victoria Excellentissima is quite limited, a table of these combinations is in order:
Arithmetic Geometric Harmonic
Possible with Evens (White) Only:
2 9 16 72 2 9 16 2:9 = 16:72 9 16 72 144/ = 16 9 2
With a Geometric Series:
3 4 6 9 3 6 9 4 6 9 3 4 6 12/ = 4 3 2
4 6 9 12 6 9 12 4 6 9 4 6 12 12/ = 3 2 1
15 20 30 45 15 30 45 20 30 45 15 20 30 60/ = 4 3 2
Other:
2 3 4 6 2 3 4 2:3 = 4:6 3 4 6 12/ = 4 3 2
2 4 6 2 3 6 6/ = 3 2 1
2 3 6 9 3 6 9 2:3 = 6:9 2 3 6 6/ = 3 2 1
2 4 6 12 2 4 6 2:4 = 6:12 4 6 12 12/ = 3 2 1
2 5 8 20 2 5 8 2:5 = 8:20 5 8 20 40/ = 8 5 2
2 7 12 42 2 7 12 2:7 = 12:42 7 12 42 84/ = 12 7 2
3 4 6 8 4 6 8 3:4 = 6:8 3 4 6 12/ = 4 3 2
3 5 9 15 3 9 15 3:5 = 9:15 3 5 15 15/ = 5 3 1
3 5 15 25 5 15 25 3:5 = 15:25 3 5 15 15/ = 5 3 1
3 9 15 45 3 9 15 3:9 = 15:45 9 15 45 45/ = 5 3 1
4 6 8 12 4 6 8 4:6 = 8:12 6 8 12 24/ = 4 3 2
4 8 12 4 6 12 12/ = 3 2 1
4 7 16 28 4 16 28 4:7 = 16:28 4 7 28 28/ = 7 4 1
4 7 28 49 7 28 49 4:7 = 28:49 4 7 28 28/ = 7 4 1
5 9 25 45 5 25 45 5:9 = 25:45 5 9 45 45/ = 9 5 1
5 9 45 81 9 45 81 5:9 = 45:81 5 9 45 45/ = 9 5 1
5 25 45 225 5 25 45 5:25 = 45:225 25 45 225 225/ = 9 5 1
6 8 9 12 6 9 12 6:8 = 9:12 6 8 12 24/ = 4 3 2
6 8 12 16 8 12 16 6:8 = 12:16 6 8 12 24/ = 4 3 2
7 12 42 72 12 42 72 7:12 = 42:72 7 12 42 84/ = 12 7 2
8 15 64 120 8 64 120 8:15 = 64:120 8 15 120 120/ = 15 8 1
8 15 120 225 15 120 225 8:15 = 120:225 8 15 120 120/ = 15 8 1
9 12 15 20 9 12 15 9:12 = 15:20 12 15 20 60/ = 5 4 3
12 15 16 20 12 16 20 12:15 = 16:20 12 15 20 60/ = 5 4 3
12 15 20 25 15 20 25 12:15 = 20:25 12 15 20 60/ = 5 4 3
15 30 45 90 15 30 45 15:30 = 45:90 30 45 90 90/ = 3 2 1
Incidentally, although the accounts I have seen of the rules do not explicitly mention it, apparently the Pyramid cannot be one of the pieces used to make a winning combination for one of the greater victories.
One description of the game notes that there was even a victory condition based on conflict between the Christians and the Turks. This appears to be the Victory of Standards described in Fulke.
This victory is based on the total of the numerical values of the captured pieces, but instead of a set goal, the player who makes the most captures wins the game. Since the numbers on the black pieces are larger than those on the white pieces in general, the totals are scaled to compensate for this as follows:
The total of the numerical values of the black pieces, not counting the Pyramid, is 1752, while the total of the numerical values of the white pieces, not counting the Pyramid, is 1312. So 12 is subtracted from each total, and the difference is divided by 10. One white standard thus equals 130 points, while one black standard equals 174 points; one wins by capturing the most standards. The criterion for when the game ends, so that the totals of captured pieces are to be compared, does not seem to be indicated in Fulke, however. One obvious possibility would be after both Pyramids have been captured.
In my opinion, the first of the three versions of Rithmomachy outlined here has a set of rules that is best suited for modern play. The capturing methods allowed include all four arithmetic operations, and are simple and consistent. The flying move ensures that the Triangles are not confined to only one out of every four squares on the board, and the Squares are not confined to only one out of every nine squared on the board. This appears to be strictly the case in the second version, and in the third version, the occasional opportunity to make a Knight's move depends on one's opponent attempting a capture by siege. On the other hand, it is only in the first version that the Rounds are confined to only one color of square, but that is not a serious problem.
Given, however, that the opponent's area of the board, in which pieces are to be placed for one of the greater victories, occupies several rows, this is only a problem for capturing.
On the other hand, the second version has a layout that seems more natural, and unlike the first version, it allows for the lesser victories. Thus, a version of Rithmomachy intended for current play might combine elements from both versions.
Using the rule of movement from the second version, but allowing pieces, when not making capturing moves, to move less than their full alotted distance, so that each piece may move to any square on the board, might be an easier rule to remember than the flying move of the original version of the game.
Some accounts of the rules of Rithmomachy have the Triangles moving three spaces and the Squares moving four, and others have a captured piece being re-entered on a later turn, in lieu of a move, as in Shogi. The former, I believe to be simply an error, but it could be that the latter does apply to some forms of Rithmomachy, either as the rules being quite variable, or that I was the one who had not understood Fulke correctly, or that this is the rule which applies to the second form of the game specifically.
Another version of the rules for the second version of the game has captured pieces becoming pieces for the opponent, but the pyramid and only the pyramid, instead of all the pieces except the pyramid. In that version of the rules, which may be due to Barozzi, the Rounds move one step orthogonally, the Triangles move two steps diagonally, and the Squares move three steps either orthogonally or diagonally. The Knight's move to escape from an attack is also present.