On the railroads of North America, normal-sized trains run on track that has 4 feet and 8 1/2 inches between the inside sides of both rails.
So a toy train at a scale of 1:48 would have track where the distance between the insides of the two rails was 1 3/32" across, right?
The gauge of a train is the distance between the inside sides of the two rails.
The scale of a train is the proportion of its size, compared to the size of the real thing.
But sometimes the gauge of a model train is not exactly to scale.
Thus, in the case of an O gauge train, the gauge is 1 1/4", not 1 3/32", but the rest of the train is designed according to a scale of 1:48.
There are two important cases where gauge and scale have parted ways.
The first is this: HO model trains have a gauge of 16.5 millimeters. Model trains that run on the same track, with a gauge of 16.5 millimeters, were sold in Britain as OO model trains.
But these two kinds of trains, although they can use the same tracks, are mismatched in size: HO trains have a scale of 3.5 mm to the foot, or 1:87.086; OO trains have a scale of 4 mm to the foot, or 1:76.2. So an OO train is about 14% bigger than a corresponding HO train.
The second is this: TT model trains have a gauge of 12 millimeters, and a scale of 1:120. But the first trains with a gauge of 12 millimeters, made and sold in Britain, had a scale of 3 mm to the foot, or 1:101.6; thus, they were about 18% larger. Sometimes these trains are referred to as being TT-3 trains.
The various sizes of model trains have had a long history.
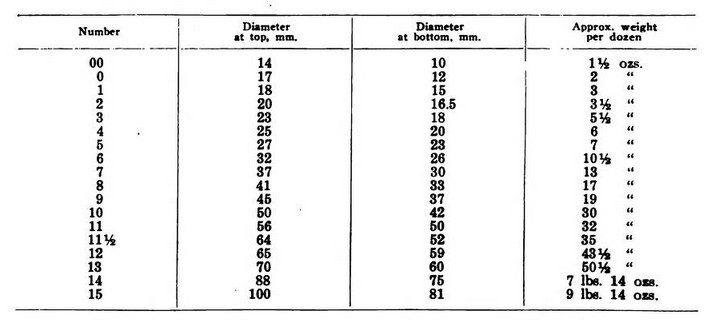
From chemistry class, or from making home preserves, at one time you may have become acquainted with the fact that corks and rubber stoppers for flasks are made in sizes such as 5, 4, 3, 2, 1, 0, 00, and 000. Thus, 00 can be thought of as an old way to write -1, and 000 as an old way to write -2.
Some of the names used for the sizes of model railroad trains originated in this fashion:
size gauge 3 2 1/2 inch 2 2 inch 1 1 3/4 inch O 1 1/4 inch OO 16.5 mm OOO 9.5 mm
although "originated" is perhaps a strong word; Märklin, a firm still in the model railroad business (having pioneered the Z gauge/scale and electronic control of individual trains) originally brought out several numbered sizes of toy trains as follows:
V 117mm IV 75mm III 67mm II 54mm I 48mm
with a 0 gauge of 35mm later added to that series. Unlike the other gauges discussed here, these measurements were between the centers of the two rails, leading to confusion in the early history of toy train manufacturing.
Incidentally, while the electronic control system developed by Märklin, initially available in 1984, eventually led to the development of the DCC system now used by several manufacturers, there were earlier attempts at remote control of trains.
The first attempt was by Lionel in 1940, the Lionel Magic Electrol, but the Second World War intervened, of course. They tried again in 1946 with Lionel Electronic Control. It involved controlling trains by radio, and it required a miniature vacuum tube in the receiver in the locomotive. This was quite expensive; still, it remained available from Lionel until 1950, and so it was not an immediate flop.
The second attempt was by General Electric in 1964, ASTRAC. This allowed up to five trains to be controlled with a signal sent over the tracks. This was a transistorized analog system, and so one had to install one of five receiving modules in each train, permanently tuned to one of the audio frequency channels used. One interesting historical tidbit is that the model train set used by the villain in the James Bond film Goldfinger was fitted with an ASTRAC system.
Some other early electronic systems were:
The Hornby system was digital, while Dynatrol and Onboard were multiplexed by frequency like ASTRAC. (I am unsure of the date on which Onboard originated; although one web page dates it from 1979, none of the mentions of it I could find predate 1983.)
The gauge is the spacing between the inner edges of the two tracks, or the outer edges of the flanges of the two wheels on an axle.
Commonly, in line with practice in other fields of model making, one tends to want to refer to different scales; one might buy a model kit in a 1/48 scale, for example. But in model railroading, the gauge is the incontrovertible fact which determines if a given train will run on a given track.
Note that 0, 00, and 000 became O, OO, and OOO, the numbers changing to letters. (This can easily be seen from the typesetting of any book on model railroading, since in almost any typeface, the letter O is visibly wider than the number 0. It certainly is true that these scales originated in a numeric form, but it is also true that their names are letters at present.) The gauge shown here as OO is also that for HO, or "half O". There was also a gauge half the size of size 1 which was called HI, the 1 changing to an I. This gauge was essentially identical to what later became known as S.
Railroad tracks in the United States, and several other countries, including most other English-speaking nations, have a gauge in real life of 4 feet, 8 1/2 inches.
One notable exception to the use of this gauge is the former Russian Empire, and its successor states such as the Soviet Union, and Russia today. Russia used a gauge of 5 feet, or 1,524 millimetres, which was officially changed to a metric gauge of 1,520 millimetres in 1970.
A gauge of 3 feet 6 inches, or 1,067mm, is the principal railroad gauge in use in several countries in Africa, as well as in Japan, Taiwan, and New Zealand.
And a gauge of 5 feet 6 inches, or 1,676 mm, is used both on the Indian subcontinent - in India, Pakistan, Bangaladesh, and Sri Lanka - and in Argentina and Chile as the principal gauge. As well, the closely similar gauge of 1,668 mm is the principal railroad gauge used in Spain and Portugal.
Thus, one can immediately derive the correct scale for any model railroad gauge by dividing this size by the gauge, right?
Unfortunately, not. Model railroad trains, for various reasons, are not entirely true to scale. Thus, "HO scale", preferred in the United States, and OO, preferred in the United Kingdom, share the same gauge of 16.5 mm, but are nominally designed to reflect two different scales: 3.5 millimeters to the foot for HO, and 4 millimeters to the foot for OO.
In addition to scale distinguishing model train sizes with the same gauge, other factors can cause a distinction. HO trains, and those of most other sizes, including S, are normally powered by the two rails having a DC voltage difference between them. O trains, however, run on track with a third rail in the middle, like some real subway trains, with the third rail supplying the voltage, and the rails bearing the wheels both providing a ground return path.
Between 1957 and 1966, Lionel offered Super O track, which was modified so that the appearance of the third rail would be less obtrusive.
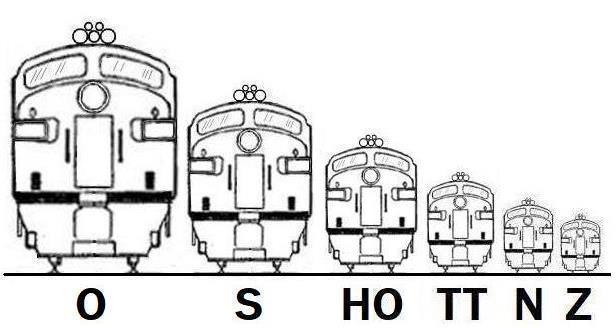
The most well-known gauges and scales are:
name gauge scale G 45 mm 1: 22.5 O 1 1/4 " 1: 48 S 7/8 " 1: 64 OO 16.5 mm 1: 76.2 (exactly) (4 mm to the foot) HO 16.5 mm 1: 87.085714... (3.5 mm to the foot) TT3 12 mm 1:101.6 (exactly) (3 mm to the foot) TT 12 mm 1:120 N 9 mm 1:160 Z 6.5 mm 1:200
The S and TT sizes are no longer common in current use, but at one time they were popular in the United States, and thus they are still relatively well remembered. The TT size is, however, still sold in some European countries, and S size trains are still readily available from one company in the United States. Also, in the United States, for a time, OO was used as the designation for trains that had the same 4 mm to the foot scale as associated with that designation in Britain, but with a 19mm gauge.
Since N gauge trains are more expensive than HO scale trains, because of the more exacting precision required in their manufacture, it would seem that the TT scale would provide greater compactness than HO scale along with lower cost than that of either HO or N, and, thus, I personally feel that it is regrettable that what appears to be the ideal scale, or at least the least expensive scale, has fallen into disuse. It may also be noted that while the TT size originated with a scale of 3 mm to the foot, a more accurate 1:120 scale has come to be associated with it as it became less popular.
If one made trains to exact scale, comparing the 4 foot, 8 1/2 inch gauge of actual trains to the various model train gauges would yield the following exact scales:
name gauge scale G 45 mm 1: 31.891111... O 1 1/4 " 1: 45.2 S 7/8 " 1: 64.571428... HO 16.5 mm 1: 86.975757... TT 12 mm 1:119.591666... N 9 mm 1:159.455555... Z 6.5 mm 1:220.784615...
Thus, it can be seen that 1:64 for S scale, 1:87.085714 for HO scale, 1:120 for TT scale, and 1:160 for N scale are very close to the exact scale implied by the gauge used.
Here is an image attempting to show the relative sizes of trains in the different gauges popular in the United States (and Canada as well) visually. The image of the train body is proportional to the scale; for the O gauge, the TT gauge, and the Z gauge, the wheelbase has been adjusted separately to conform to the gauge.

Since N scale trains tend to be more expensive than HO scale trains, because of the increased difficulty of finer scale workmanship, despite the need for less material, but people would like to have more compact train layouts, would the TT scale be a good compromise between a smaller size and a tight budget?
Incidentally, I'm not the only person to have thought of this, I have learned: Mark Sazavsky, living not far from me in St. Albert, Alberta, invested a considerable sum of money in having some new TT gauge locomotives made by a major model train manufacturer; unfortunately, as the web site of his enterprise appears no longer to be active, and from other information I've seen on-line, despite there being a thriving community of TT enthusiasts out there, his venture has not yet met with much success.
In Britain, trains referred to as TT gauge trains are normally designed to a scale of 1:101.6, not 1:120, although their gauge is still 12mm. This makes matters more confusing than in the case of HO gauge and OO gauge, where both types of train have a gauge of 16.5 mm, but the one at 1:76.2 scale is called by one name, OO, and the one at about 1:87 scale is called HO.
The 1:101.6 scale, of 3mm to the foot, may not have been the original TT scale, but instead just one used in Britain. In Eastern Europe and the Soviet Union, where TT scale was popular, there was also a mismatch with the prototype, but in the opposite direction, a 1:130 scale being used. This is similar to what I noted above, that TT started out as 1:101.6 but changed to 1:120, so I will need to verify whether the original HP Products trains were at 1:101.6 or not, to determine whether Britain retained, or originated, that larger scale.
Some searching has disclosed the answer. HP Products in the U.S. indeed made their trains to the 1:120 scale from the start. However, trains with a 1:101.6 scale of 3mm to the foot, on a 12 mm gauge track, sold as "Table Top" trains, were originated in Britain before World War II by one Stewart Reidpath, so Britain, not the U.S., was where TT gauge originated, and 1:101.6 was its original scale, flawed though it may be.
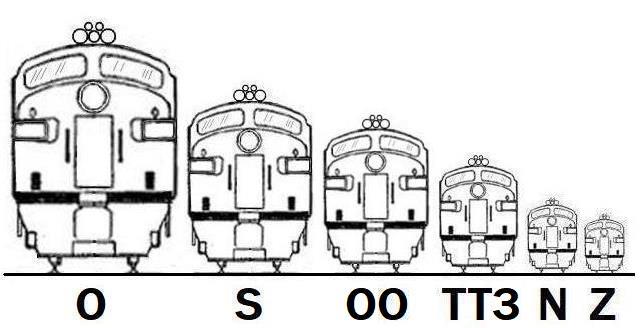
The designation TT3 is sometimes used for TT gauge with the 1:101.6 scale to distinguish it from 1:120 TT. And, indeed, I've just looked at a British model railroading magazine from 1964, where TT-3 is used for that, and in which 1:120 TT gauge trains from Zeuke in (West) Germany were advertised.
So to reduce the chance of confusion, I've used the TT3 designation in the diagram below, showing the relative sizes of the train gauges popular in Britain:
Trains made for specialized purposes, such as hauling ore from mines, often had a much narrower gauge than the 4' 8 1/2 " of ordinary railway trains. For convenience, instead of having trains and track manufactured to the exact gauge of such trains when taken to scale, railroad modellers have used track designed to represent conventional railway trains in a smaller scale, and used it as the track for narrow-gauge trains in a layout using one of the other conventional track sizes for regular trains.
While less serious model railroaders can treat the gauge as the given, and mix HO and OO equipment with abandon, when it comes to narrow-gauge equipment, it is clearly the scale that is the given; it is the equipment that would be found in the same layout that should be grouped together in a chart.
Wikipedia lists two attempts by Japanese manufacturers to make trains even smaller than the Z gauge:
name gauge scale ZZ 4.8 mm 1:300 T 3 mm 1:450
ZZ was originated by Bandai, a well-known manufacturer of toys associated with popular anime characters, and T was originated by Eishindo.
However, T gauge is more than just an attempt; I've found web sites currently offering T gauge trains by Eishindo for sale.
An article in the September, 1954 issue of Popular Science about TT scale trains, then newly originated by Hal Joyce, mentioned two smaller scales, HH, from Sweden, and OOO, in use in Britain.
name gauge scale HH 9.6 mm 1:150 OOO 9 mm 1:152.4 (2mm to the foot)
The HH scale is also mentioned in an article in the May, 1946 issue of Model Railroader. Note that the scale and gauge are exactly twice those of ZZ. That article refers to this size of train having been manufactured briefly in Stockholm from 1942 to 1943.
In the case of OOO scale, I have seen contradictory information from several references on-line.
However, I have managed to find original references showing that, at least in 1963, Lone Star was making trains, designated OOO, that ran on 9mm track and which were electrically powered, and furthermore trains by Arnold (now Arnold-Rapido) that ran on 9mm track were sold in Britain as OOO gauge.
In addition to O, OO, and OOO representing 0, 00, and 000 as a notation for 0, -1, and -2, some of the other scale designations have meaningful origins.
S stood for "sixty-fourth", as it had a nominal 1:64 scale.
TT stood for "table top", as it made smaller layouts possible.
N stood for "nine millimetre", as that was its gauge.
The smaller gauges of train, of course, were introduced later.
OO gauge trains apparently were originated by Bing, a German model train firm, in 1924, although it was only many years later that HO model trains made their appearance in North America; Hornby introduced OO in Britain in 1938, and American Flyer seems to have been the first American company with HO, also in 1938.
The year 1946 saw the introduction both of S gauge trains, by American Flyer, and of TT gauge trains, sold by the firm of HP Products, founded by Hal Joyce.
The modern 9mm gauge appears to have originated in 1960, first called OOO before it was renamed N.
And the Z scale is due to Märklin, and dates from 1972.
As I mentioned, in the real world, there are trains with a gauge smaller than the 4 foot, 8 1/2 inch standard gauge. These trains are sometimes addressed by railway modelers as well, and naturally, to take advantage of commercially available parts, often the one train gauge is used at the scale of the next larger common train gauge.
Some examples of such gauge and scale combinations are:
Primary Gauge of smaller trains at that scale
Scale
S HO TT N Z
O Oe On1.5
S Sn3.5 Se
OO OO9
HO HOn3.5 HOn2.5 HOi
TT TTe
N Nn3
Note that just as OO and HO, which both run on 16.5 mm track, have different names because the scale is different, so are there different names for narrow gauge trains which work with those normal gauge trains, running on 9 mm track, with different scales.
Of course, it is simply an expedient to use a commonly-available model train gauge for narrow-gauge trains, and thus there are also tracks and trains available with specialized gauges that are closer to the actual size of the narrow-gauge track being modelled taken to the scale as would apply to any normal gauge trains in the same layout.
I remembered reading, in a book on model railroading from the 1960s, that the standard railway gauge of 4 feet, 8 and 1/2 inches, also known as Stephenson Gauge, and also given as 1435 mm (although 4 feet, 8 1/2 inches would be exactly 1435.1 mm), corresponded to the ruts left in the ground by wheeled vehicles used in the Roman empire; this appears in one reference from 1958 that I have recently run across, as well as one from 1914; but in the latter, it is only noted as a supposition. However, I have since learned that this is an "Internet myth"; at least I can add that myth though it may be, it is a myth that long predates the Internet.
According to those sites, the truth was that George Stephenson decided on a width of five feet for the railroad tracks for his locomotive, and that led to a gauge of 4' 8" since the rails were two inches wide. But he had to add a half inch for some practical reason.
However, the reason that he started with five feet was that it was in the same ballpark as the width of the wheelbase of horse-drawn carriages in his vicinity. And Rome once ruled Britain, and so the wheels of the horse-drawn carriages he saw could well have been determined by a continued need for compatibility with the ruts continuing to be made by earlier generations of carts, each one compatible with the one before, down to the first ones which followed the Roman standard.
But since the figure of five feet was just an arbitrary one to give a roughly similar size, with no attempt to exactly match what was used for horse-drawn carts, while there is a very limited connection to ancient Rome still remaining, I agree that it is legitimate to say that at George Stephenson, there was a break in continuity, and the Roman axle standard is not really preserved by present-day railroads.
Initially, when I read that his son testified under oath, on August 6, 1845, to a Parliamentary inquiry on the question of what common railroad gauge should be adopted in Britain that the 4' 8 1/2" gauge was not devised by George Stephenson himself, but rather that he had adopted the gauge already in use by existing railways in the area of Newcastle-upon-Tyne, I had thought this cast some doubt upon that story. This testimony, however, was in answer to a question about a railway on which construction started in 1826, the Liverpool and Manchester Railway. George Stephenson first chose the gauge of 4' 8 1/2" for the Stockton and Darlington railway, in 1821, having used 4' 8" for a previous one, the railway used for the Hetton colliery, and, thus, the gauge in use five years later around Newcastle-upon-Tyne could have taken its inspiration from George Stephenson's earlier railway.
A book from 1868, The Life of George Stephenson, and of his son, Robert Stephenson; comprising also a history of the invention and introduction of the railway locomotive, by Samuel Smiles, states:
When forming the road, the proper gauge had also to be determined. What width was this to be? The gauge of the first tram-road laid down had virtually settled the point. The gauge of wheels of the common vehicles of the country - of the carts and wagons employed on common roads, which were first used on the tram-roads - was about 4 feet 8 1/2 inches. And so the first tram-roads were laid down of this gauge.
which supports the story of this coming down from Rome.
The distance between the centres of the ruts left by Roman carts apparently was measured as 4' 9", which is rather close, though. A Roman foot was about 11.65 inches (296 mm) in length, though the surviving examples on which this was based varied from 292 to 300 mm, and so that distance would be 4 feet and 14 1/4 digits, or 4 feet and 10 3/4 inches, which is not a round number in their measure. Another source gives the gauge of Roman carts as 1.42 metres, only 15mm smaller than Stephenson Gauge, which would be about 4' 9 1/2" in Roman measure, and about 4' 7.9055" in normal English units, very close to the 4' 8" that Stephenson originally used. The standard is supposed to have dated back to the very beginning of Roman Law in the Twelve Tables, but I have not yet been able to locate a source for the Roman standard stated in Roman units of measure, if, indeed, it had been stated in that form.
So, at this point, I suspect that the urban legend, as it were, had some truth to it. The ancient Romans standardized the axles of carts in their empire to avoid trouble with wheel ruts; this was preserved by carts in England, and thus George Stephenson used that same gauge, 4' 8", for a tramway at Killingworth and for the Hetton colliery. But for the first railway that accepted passengers and offered freight services to the general commercial trade, the Stockton and Darlington railway, George Stephenson intentionally departed from the traditional gauge, if only by a trifling half inch, so that the steam engine he wished to use would fit between the wheels instead of having to be lifted up, or some such thing.
With the starting point being 4' 8", and not 5', however, the half inch becomes less of a break in continuity, and thus it seems that, with a small note of the details involved, the myth turns out to be true.
As noted, smaller gauges are used for some special-purpose railways. A narrower gauge, for example, allows railroad tracks to bend around sharper corners, useful for trains taking ore from mines in mountainous areas.
Before the adoption of a uniform standard gauge for general-purpose train service, there were trains with a 5' 3" gauge in Australia, and it would seem quite reasonable that so small a difference would have little technical benefit to outweigh the problems caused by having different gauges. In Britain, however, there were tracks with a gauge of seven feet, and in that case, it at least seems possible that such rails could have made possible a new generation of larger and more advanced locomotives.
Wikipedia notes that, before the adoption of the metric system in nearly all countries except the English-speaking ones, most of which, of course, also adopted the metric system later, with the exception of the United States of America, some other countries used their own units in defining railway gauges.
Thus, a Prussian foot of 313.8536 mm was used to define a railway gauge of 2 1/2 Prussian feet, a Swedish foot of 296.904 mm was used to define a railway gauge of 3 Swedish feet, a Portuguese foot of 332.8 mm was used to define a railway gauge of 5 Portuguese feet, and a Castilian foot of 278.6 mm was used to define a railway gauge of 6 Castilian feet.
Another important dimension in model railroading is the height of the rails. This is not a constant for a given gauge.
For an HO railroad, one might use Code 100 track or Code 83 track. These terms mean that the rails are 0.1" high in the case of Code 100, and 0.083" high in the case of Code 83.
Code 100 was originally the most common type of track used with HO scale model railroads, but today, as tastes have shifted towards a more realistic appearance, Code 83 has become the most popular. Code 70 is also available in HO.
However, real railways use different sizes of rail depending on the nature of traffic expected on a route. Thus it is possible to build a layout with a size of rail that corresponds to what the real-life railway one is modelling would use.
For N scale, Code 80 was originally the most common size of track, and Code 55 is currently more popular. Code 65 is also available. For TT scale, Code 83 and Code 70 seem to be the most easily available.
HO scale TT scale N scale Prototype rail
Code 80 12.8" 227 pound
Code 70 11.2" 198 pound
Code 65 10.4" 180 pound
Code 83 9.96" 175 pound
Code 80 9.6" 170 pound
Code 55 8.8" 156 pound
Code 100 8.7" 152 pound
Code 70 8.4" 142 pound
Code 83 Code 60 Code 45 7.1" 132 pound
Code 76 Code 55 Code 41 6.6" 115 pound
Code 40 6.4" 114 pound
Code 70 Code 50 Code 38 6" 100 pound
Thus, due to the smaller size of N scale, the more "prototypical" Code 55 is still bigger than the old Code 100 for HO. The weights are the weight of the rail itself in pounds per yard. If one were searching for an ideally prototypical look, in 1960, the most common type of track was at 115 pound weight or so, while in 1940, it was 95 pound weight or so, and so the rail sizes for 115 pound and 100 pound weight are filled in, even if they are unrealistic in most scales.
In the era of steam trains, many different configurations of locomotives were made to meet different needs. These configurations came to be described in a standardized notation. Thus, a 4-6-2 steam locomotive was one that looked like this:
__ ___
____||__| |
(__________|
/ ooOOOo |
This numerical notation, showing four pilot wheels in two pairs before the six drive wheels in three pairs, and a trailing truck consisting of two wheels in one pair, for a 4-6-2 locomotive, is called the Whyte system.
The different configurations of steam locomotive also had names, some of them are:
2-6-0 Mogul 2-8-0 Consolidation 2-10-0 Decapod
2-4-2 Columbia 2-6-2 Prairie 2-8-2 Mikado 2-10-2 Santa Fe
2-8-4 Berkshire 2-10-4 Texas
4-4-0 American 4-6-0 Ten-Wheeler 4-8-0 Twelve-Wheeler
4-4-2 Atlantic 4-6-2 Pacific 4-8-2 Mountain 4-10-2 Overland
4-6-4 Hudson 4-8-4 Northern
Some of these names had alternates: the American was just called an Eight-Wheeler in Canada; the Mikado was briefly renamed the MacArthur during the Second World War; and the Northern was called the Niagara, or by other names, in the South.
The demand for more powerful locomotives led to the construction of articulated locomotives. In the Whyte system, these were described by using four numbers: the number of pilot wheels, the number of drive wheels before the articulation point, the number of drive wheels after the articulation point, and the number of wheels in the trailing truck.
Configurations of that kind were:
2-10-10-2 Virginian
2-6-6-4 Class A
2-6-6-6 Allegheny
4-6-6-4 Challenger 4-8-8-4 Big Boy
A short page has now been added to the site with a few more words about the history of the locomotive.
I had not thought that listing the sizes of corks or bottle stoppers would be all that interesting to be worth the trouble of finding out to include here, but as I was able to find a list of the sizes of rubber stoppers for use in chemistry without too much difficulty, here it is:
But another series of sizes associated with letters happens to be connected to one of life's greatest mysteries!
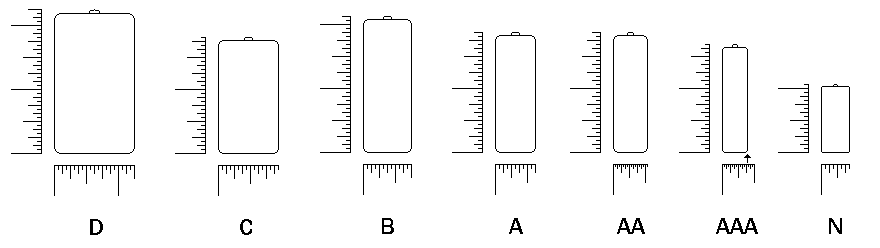
When you go to the store, you may often see dry cells offered for sale for use in various forms of electronic or electrical equipment.
There will usually be D cells, C cells, AA cells, and AAA cells.
Since one also sometimes sees the small N cells, I've included them in the diagram above as well.
But you will never see B cells or A cells. What happened to them, and what size were they?
Well, I found out the standard sizes of the different kinds of battery.
The sizes are illustrated in the diagram above, but here is also a table of them:
Height Width
D 2 1/4 1 1/4
C 1 13/16 15/16
B 2 1/8 3/4
A 1 7/8 5/8
AA 1 7/8 17/32
AAA 1 11/16 25/64
N 1 1/16 7/16
And from those sizes, the reason for the disappearance of A cells and B cells is fairly obvious. The B cell, while slimmer than the C cell, is actually taller than it. The A cell is the same height as the AA cell, only a little wider than it.
Clearly, then, what happened was this: on the one hand, there was a pressing need for smaller batteries for more portable devices; on the other hand, the technology needed to make smaller batteries that would still have a reasonable battery life was only advancing at a painfully slow rate.
This led to the B cell, and then the A cell, and then the AA cell, all being defined even though each one was only slightly smaller than the one before. So once the AA cell became established, the B cell and the A cell fell into disuse, the jump between the C cell and the AA cell being large enough to make a noticeable difference, but small enough that no in-between sizes were really needed.
Note from the diagram that these battery sizes were originally defined in terms of inches, even if they are now specified in millimetres.