This table converts fractional 16ths of an inch into decimal inches and centimeters.
inches centimeters 1/16 0.0625 0.15875 1/8 0.125 0.3175 3/16 0.1875 0.47625 1/4 0.25 0.635 5/16 0.3125 0.79375 3/8 0.375 0.9525 7/16 0.4375 1.11125 1/2 0.5 1.27 9/16 0.5625 1.42875 5/8 0.625 1.5875 11/16 0.6875 1.74625 3/4 0.75 1.905 13/16 0.8125 2.06375 7/8 0.875 2.2225 15/16 0.9375 2.38125
Note that the equivalents in centimeters are exact, as one inch is 2.54 centimeters long. In the U.S., before 1964, it was instead the case that a meter was exactly 39.37 inches long, making the inch slightly larger than 2.54 centimeters; and in the British Commonwealth, the inch was slightly smaller than 2.54 centimeters, being defined on the basis of an independent physical standard.
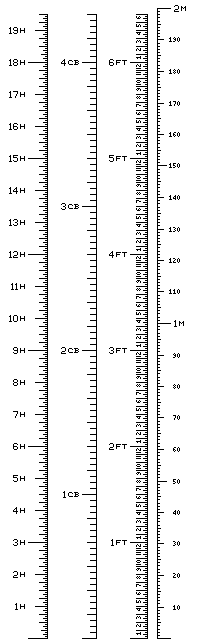
If we're dealing with conversions between the English and metric units of length, a handy conversion chart such as that shown at right may be useful. It also embraces conversions from the height of horses, expressed in hands, and from a cubit of 18 inches in length.
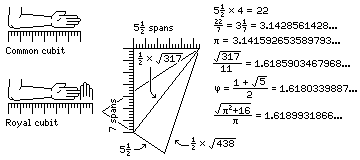
In a cubit, four digits (each 3/4 inch long) make a span (three inches) and six spans make a cubit. In addition to the span being based on the width of a finger, and matching the spaces between the keys on a typewriter or computer keyboard, the cubit is based on the distance between the elbow and the tips of the fingers, as this diagram illustrates:

It also illustrates the existence, in ancient Egypt, of a royal cubit of seven spans in length, which figured in the construction of the Great Pyramid, accounting for the seeming appearance of the mathematical constant pi in its design, when what happened was that its approximation 3 1/7, closer to the one actually in use in Egypt in those days, simply appeared by a coincidence.
As typewriters typically print with six lines to the inch, another group of fractions of an inch is often used. Here, even the decimal inches usually cannot be exact
inches centimeters 1/6 0.1666667 0.4233333 1/3 0.3333333 0.8466667 1/2 0.5 1.27 2/3 0.6666667 1.6933333 5/6 0.8333333 2.1166667
One common complaint about the metric system is that it doesn't provide a natural way to divide things into thirds; even dividing things into quarters requires one to go down two levels, instead of just one, in the system of units, since 0.25 is the decimal that represents 1/4.
The metric system did not divide the day into 100,000 parts; instead, the hour, minute, and second were retained to allow the day to be divided neatly into quarters and thirds.
In response to an instance of the occasionally-heard suggestion that the metric system should have been built on base 12 instead of base 10, it occurred to me that the precedent of an everyday unit, the day, standing in such a relationship to the metric unit, the second, that the day can be exactly divided into 27 parts, each of which consists of an even number of seconds (3200 seconds, or 53 minutes and 20 seconds), one could, for example, use as everyday units a metric pound of 453.6 grams (instead of approximately 453.69 grams) and a metric inch of 2.52 centimeters (instead of 2.54 centimeters).
453.6 grams divides evenly into 81 units of 5.6 grams, and also into 7 units of 64.8 grams - and, for that matter, into 8 units of 56.7 grams. 2.52 centimeters divides evenly into 9 units of 0.28 centimeters, and also into 7 units of 0.36 centimeters - and, for that matter, into 4 units of 0.63 centimeters.
However, I can't really expect that this very wild idea of using this metric pound and metric inch as everyday units, and measuring things out in these pounds and inches, so that they can be evenly divided into thirds, ninths, and sevenths if one uses the regular metric scale, would catch on.
Another interesting pair of units of length are the light-year and the parsec. The speed of light is now exactly 2.99792458 * (10^8) meters per second by definition. With astronomers, however, there are many kinds of year; the tropical, the sidereal, the anomalistic, and the Gregorian calendar year. As it happens, the light-year is, according to Wikipedia, the distance light travels in a Julian year of 365 1/4 days, which is 9.4607304725808 * (10^15) meters.
The astronomical unit is 149,597,870,691 metres, give or take 30 metres. Since the intent of the parsec is to permit one to calculate the distances to celestial bodies from their parallaxes, simply by taking the reciprocal of the parallax, and these bodies are all be at distances greater than 1 parsec, it might actually be more reasonable to use the reciprocal of the angle in radians rather than calculating the cotangent of one second of arc exactly. With the exact cotangent, a parsec is approximately 20264.806245480 astronomical units in length; if one takes the reciprocal of the angle, it would be 206264.806247096 astronomical units in length, for a difference of .000001616 astronomical units.
Based on the cotangent, a parsec is 3.08567758128 * (10^15) metres, give or take about 600,000 metres, and so a parsec is approximately 3.26156377694566 light years, a figure that one does not usually see quoted to this precision.
The topics associated with units of measurement go in many directions, and so the discussion continues on several other pages.