
The frequency of a resonant circuit can be calculated from the formula:
1
f = ------------------------
2 * pi * sqrt( L * C )
where f is the resonant frequency in Hertz (or cycles per second), L is the inductance in Henries, and C is the capacitance in Farads.
Since a microhenry is 10^(-6) henries, and a picofarad is 10^(-12) farads, if we use those units in the formula above, then the frequency f would be in units of 10^9 Hertz, or Gigahertz, since 9 is half of 18.
On the other hand, as a millihenry is 10^(-3) henries, and a picofarad is 10^(-12) farads, then, since 15 is not an even number, we would have to amend the formula somewhat if we wished to use those units:
5.0329212104487... 1
f = --------------------- = -------------------------------
sqrt( L * C ) 2 * pi * sqrt( .001 * L * C )
If we divide the square root of 1000 by 2 * pi, we get a number that is about 5.033. The result of the formula will be a resonant frequency measured in megahertz.
One might, typically, obtain inductors whose inductance is given in millihenries, and the most common variable capacitor used to tune radios to the desired station might have a capacitance which can be varied from 365 picofarads down to a minimum amount variously specified as 9 picofarads, or 14 picofarads.
One source notes that such a capacitor is typically used in conjunction with an inductance of 250 microhenries when used to tune the AM broadcast band. As this band conventionally consisted of stations with carrier frequencies ranging from 540 kHz to 1600 kHz, This works out to a range of capacitances from 347.46 pF to 39.58 pF.
In a radio designed to receive short-wave signals, however, a special variable capacitor might be used with a ganged component going up to 100 or 200 pF for use in receiving short-wave signals.
For our purposes, what is important is that the resonant frequency of an LC resonant circuit is proportional to one over the square root of the capacitance. Combining that fact with the fact that variable capacitors are so designed that their capacitance is linearly proportional to the angle through which the control knob is turned, we are in a position to determine what the tuning dial for a radio might look like.
An AM radio, covering the frequency band which is known as "medium wave" in Europe, allows one to tune in radio stations whose frequencies vary from 540 kHz to 1600 kHz. The actual frequency range allocated to the AM band extends from 535 kHz to 1605 kHz because an AM radio station uses a range of frequencies centered around its carrier frequency in order to transmit the desired audio signal. The tuning dial on an AM radio may also have a larger range than 540 kHz to 1600 kHz, to allow for possible errors in the construction or adjustment of a radio.
This involves a ratio of about 3:1 in frequencies.
Originally, in the United States, radio stations were spaced apart in frequency by 10 kHz, while in Europe they were spaced by increments of 8 kHz. Recently, to allow more AM radio stations to be licensed, the spacing of AM radio stations in the United States was changed to 9 kHz. Another change is that the frequency range allocated to the AM band was extended upwards to 1700 kHz; a few older AM radios already extended upwards to this frequency. Since newer radios tend to have digital displays instead of dials, I have let the diagrams be based on the older frequency ranges which applied back in the days when radios had dials.
Using the formula above, since the frequency is proportional to one over the square root of the capacitance, one can also conclude that the capacitance is proportional to one over the frequency squared.
On a tuning dial, for frequency to increase from left to right, the capacitance must decrease when the dial is turned in that direction.
We can then calculate where a dial must be turned to reach the various possible frequencies on a dial for the AM band:
Frequency 10^6/(f^2) angle 540 3.43 0 600 2.78 38.6 640 2.44 58.5 700 2.04 82.3 800 1.56 110.6 900 1.23 130 1100 .83 154.2 1240 ,65 164.6 1400 .51 172.9 1600 .39 180
However, if you look at a typical AM radio, the halfway point, instead of being just above 700 kHz, is usually just below 900 kHz. The high frequencies are closer together than the lower frequencies on the dial of such a radio; so while some compensation for the crowding of the upper end of the band is being performed, this compensation is only partial.
A variable capacitor consists of several metal plates, all equally spaced, in two alternating groups, one moved by the shaft which the tuning knob turns, the other group fixed.
The two types of plate can have the kind of profile shown below:

In this type of arrangement, the area of overlap, and hence the capacitance, is directly proportional to the angle of rotation. However, other possibilities exist.
For example, if the outer curve on the plates were to correspond to an Archimedian spiral, then the capacitance would be proportional to the cube of the angle of rotation plus some constant. This is because a small rotation adds or removes a wedge-shaped area from the area of overlap, and the area of a triangle, if its shape is not altered, is proportional to the square of its height or any other dimension.
Let us instead try a spiral where distance from the center, instead of increasing linearly with angle, increases as the square root of the angle. Then the amount by which a small rotation changes the capacitance will increase linearly with angle, and thus the capacitance will be proportional to the square of the angle.
This isn't quite what is wanted: the angle of rotation, being proportional to the square root of the capacitance, is also proportional to the reciprocal of the frequency. This makes it proportional to the wavelength, and thus a variable capacitor of this type is called a "straight line wavelength" variable capacitor.
Prior to 1923, radio dials indicated the wavelength, rather than the frequency, of the radio station being tuned, at least in the more elaborate consumer-oriented sets where the tuning dial was marked other than in arbitrary gradations. Bandwidth, which measures the amount of information that broadcasts can include, is determined by frequency spacing, which is the primary reason that it is frequencies, not wavelengths, that are today allocated to broadcast stations. Originally, it may have been the fact that units of length are in daily use by ordinary people, while frequency was something dealt with only in specialized fields such as electronics, that led to this. If so, the fact that radio wavelengths were measured in meters may have helped to hasten the conversion to frequency in the English-speaking countries, as meters, unlike feet and inches, were hardly less exotic than cycles per second there.
One effect of this type of variable capacitor is also to moderate the crowding of frequencies at the upper end of the dial, since now a 1/(f^2) law is replaced by a 1/f law.
The reason a square-root spiral, where the rate of change of area under the spiral increases uniformly with angle, provides capacitance proportional to the angle squared is, of course, the fact that:
_x
/
| 1 2
| u , du = --- x
| 2
_/
0
and so, by the Fundamental Theorem of Calculus, it is also due to the fact that
d 2
--- x = 2x
dx
and that means we can work out the kind of spiral required for a variable capacitor with a straight line frequency characteristic:
d 1 -2
--- ----- = -----
dx 2 3
x x
This requires a variable capacitor that is more drastically eccentric.
When a capacitor is placed in parallel with a variable capacitor with a straight line wavelength characteristic, then the total capacitance is proportional to the angle squared plus a constant, of course. But one can put both a fixed capacitor, and a suitably-sized capacitor with a uniform change of capacitance with angle in parallel with a variable capacitor with a straight line wavelength characteristic to retain the straight line wavelength property. A variable capacitor with several ganged segments, one of them having a straight-line wavelength characteristic for a band having a large ratio between the highest and lowest frequencies, and several segments, each one having half the capacitance of the one before, with a straight-line capacity characteristic, can offer great flexibility.
The principle behind this is illustrated by the diagram below:
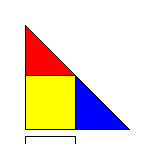
The black scale at the bottom shows the range of angles through which the capacitor can be adjusted. The diagram is a graph of the rate of change of capacitance with angle, and so at any angle, the total capacitance is the area of the triangle to the right of the point on the scale to which the capacitor is adjusted.
The area of the red triangle shows the amount of capacitance that increases with the square of the angle. The yellow triangle shows the amount of capacitance that increases in proportion to the angle. The blue triangle shows the minimum capacitance of the variable capacitor, including the capacitance placed in parallel with it.
A real variable capacitor with a straight-line wavelength characteristic will always have a minimum capacitance, contributing to the blue area, and thus will need to have a nonzero rate of change of capacitance even in its minimum capacitance position, thus contributing to the yellow area. But when additional capacitance is added in parallel, enlarging the blue area, then one can maintain a straight-line wavelength characteristic by placing ganged straight-line capacity segments in parallel as well.
In practice, however, while variable capacitors with a number of ganged segments have been used, the general practice in multi-band radios has not been to go to great lengths to achieve a consistent straight-line wavelength characteristic for different bands with different ratios of high to low frequency. The fact that in a band having a smaller frequency range, the crowding of the lower frequencies would be still further reduced by using only a fixed capacitor in parallel with a variable capacitor designed for the AM band was not seen as a bad thing.
Recently, at least in the United States, the AM band was extended to 1700 kHz; many older radios also took the AM band up to that frequency, and at one time the area just above the AM band was used by police radios. Also, radios made from 1953 to 1963 had little triangles indicating 640 kHz and 1240 kHz, the frequencies which were allocated for use through the CONELRAD system in the event of a national emergency such as a nuclear war.
Similarly, the range through which an FM radio is tuned varies from 88 MHz to 108 MHz. The ratio between high and low frequencies here is less than 1.25:1.
In Europe, a long-wave band, extending from 150 kHz to 270 kHz, is used for broadcasting. Here, the ratio of frequencies is 1.8:1. When FM radio was first introduced in North America, the frequency range from 42 to 50 MHz was used for it, involving a ratio of under 1.2:1, but that frequency range is now used for other purposes.
This is tied in with the interesting history of TV channel frequency allocations in the United States. When 6 MHz channels were originally allocated to television, instead of the current 525-line system, first a 343-line system, and then a 441-line system was used which was otherwise similar - 60 fields per second with interlacing for 30 frames per second. However, the audio portion of the signal was broadcast in AM rather than FM. The 343-line system was used for test broadcasts, but 441-line sets were sold commercially.
And 19 television channels were allocated in the VHF region of the spectrum, from 30 MHz to 300 MHz, as shown in the diagram below:
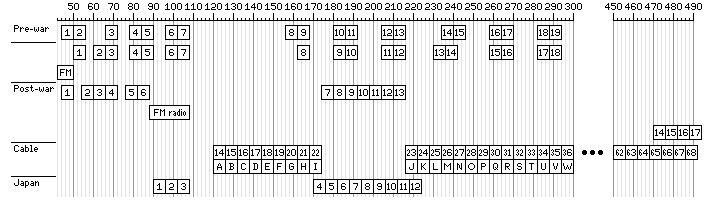
The original FM band was then allocated shortly before the United States entered World War II, leading to significant changes in the allocation of TV channels. In order that channels would remain consecutively numbered from channel 1, many channels simply had their number moved to the next channel, but a few channels were shifted in frequency. The current 525-line standard was adopted on July 1, 1941, some time after the channel allocations were changed.
Both the Great Depression and World War II would have meant by themselves that commercial TV broadcasting had not gone beyond those who today would be termed "early adopters", but in addition early TV broadcasting was limited in scope because it was only licensed as an experimental service for most, although not all, of its history prior to when the allocation of TV channels was almost completely transformed after the war. Of today's TV channels, only channels 4, 8, 9, 12, and 13 (and possibly channel 3) could be received on an antique TV set whose tuner corresponded to the former standards. And, of course, channel 1, despite the space it used no longer being occupied by FM radio, was dropped after a mere two years because of the requirements of other, non-broadcast, radio services; ironically, it was another channel common to the post-war frequency allocation and the original pre-war scheme.
UHF channels, from channel 14 upwards, are in consecutive 6 MHz bands starting with channel 14 at 470 MHz to 476 MHz; these channels were introduced in 1952, although they did not become widely used until later; in 1964, in the U.S., television sets were required to include UHF tuners. A few years ago, in 1983, UHF channels 70 through 83 were discontinued, the frequencies they occupied being reallocated to the Land Mobile Radio Service; subsequently, in 2009, still more channels, from 52 to 69, were removed from UHF television to become the 700 MHz band for cellular telephones; two years later, in 2011, channel 51 was also removed to prevent interference; and then in 2019, channels 38 through 50 also had their bandwidth transferred to cellular telephones. Thus, originally the highest-frequency UHF channel was channel 83 at 884 MHz to 890 MHz, and later it became channel 69, at 800 MHz to 806 MHz, and now it is channel 36, at 602 MHz to 608 MHz.
Also, from the inception of the UHF band in 1952, UHF channel 37, from 608 MHz to 614 MHz was withdrawn from use, so that frequencies in this band would be available to radio astronomy. This is not the region of the 21-centimeter hydrogen line, which is at 1420.4 MHz.
Brazil uses the same TV channels as are currently used in the United States and Canada, although it uses the PAL method rather than the NTSC method of encoding color information in TV broadcasts. Japan, on the other hand, uses exactly the same TV standard as North America, but, as shown in the diagram, uses different frequencies for the VHF channels. The Japanese UHF television band also starts at 470 MHz; the only difference is that its first channel is called channel 13 in Japan, since the 12 VHF channels in Japan are just numbered 1 through 12, Japan not having as involved a history of the development of television as the United States.
Also shown on the diagram, both with the channel numbers usually used, and by their official letter names, are the channels A through W, or 14 through 36, that are used for cable TV.
On the next page, I briefly look into other television systems and the techniques used to add color to television, and then I go into greater detail in the context of some ideas I had about how to combine the advantages of NTSC and PAL.
Older short-wave radios simply divided up the entire short-wave spectrum from 3 MHz to 30 MHz, as well as the remaining portion of the medium-wave region, from 1.6 MHz to 3 MHz, into a small number of bands, whose extent was arbitrary, depending on how the manufacturer of the radio wished to divide up this nearly 20:1 range of frequencies into manageable pieces. Newer short-wave radios intended for the general consumer may only provide specific frequency bands which are used for broadcasting. The various broadcast bands both in the short wave range and in the part of the medium wave range above AM radio are shown below:
From the web On one radio
120 metres 2.3 MHz - 2.498 MHz
90 metres 3.2 MHz - 3.4 MHz
75 metres 3.95 MHz - 4 MHz
60 metres 4.75 MHz - 5.1 MHz
49 metres 5.875 MHz - 6.2 MHz 5.85 MHz - 6.2 MHz
41 metres 7.1 MHz - 7.45 MHz 7.15 MHz - 7.5 MHz
31 metres 9.4 MHz - 9.915 MHz 9.45 MHz - 9.9 MHz
25 metres 11.6 MHz - 12.095 MHz 11.45 MHz - 12 MHz
22 metres 13.57 MHz - 13.87 MHz
19 metres 15.07 MHz - 15.8 MHz 15.1 MHz - 15.5 MHz
16 metres 17.48 MHz - 17.9 MHz 17.5 MHz - 18 MHz
15 metres 18.9 MHz - 19.02 MHz
13 metres 21.45 MHz - 21.85 MHz 21.45 MHz - 22 MHz
11 metres 25.6 MHz - 26.1 MHz
As these particular frequency bands for international broadcasting have existed for a long time, even when short-wave radios covered the entire short-wave spectrum, they may have included tuning aids specifically oriented to these bands, or to another set of bands within the short-wave spectrum, the amateur bands:
160 metres 1.8 MHz - 2 MHz 80 metres 3.5 MHz - 4 MHz 40 metres 7 MHz - 7.3 MHz 30 metres 10 MHz - 10.15 MHz 20 metres 14 MHz - 14.35 MHz 17 metres 18.068 MHz - 18.168 MHz 15 metres 21 MHz - 21.45 MHz 12 metres 24.89 MHz - 24.99 MHz 10 metres 28 MHz - 29.7 MHz
The older general-coverage radios would often include a fine-tuning knob to assist in finding stations in the crowded short-wave bands, or a gear arrangement might be used so that several turns of a tuning knob would be required to take the shaft of the variable capacitor through its full 180 degree range.
Here is an example of what the tuning dial of a radio might look like, if a variable capacitor with a straight line wavelength characteristic is used for tuning most of the bands, but a smaller variable capacitor with a linear relationship between capacitance and angle turned is used for the FM band:
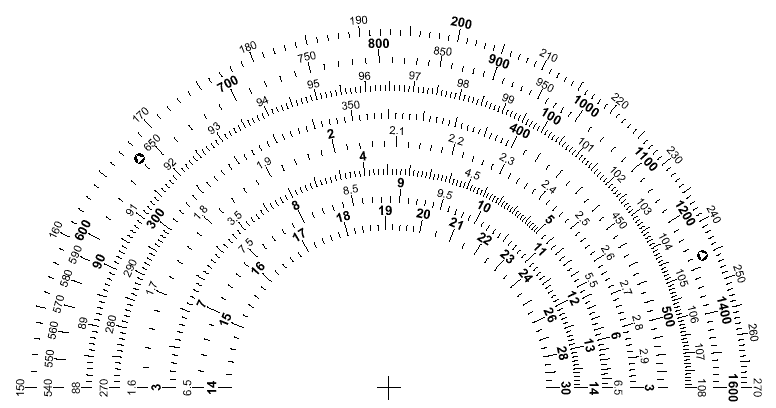
In this example, the bands provided are:
150 kHz - 270 kHz LW broadcast 540 kHz - 1600 kHz AM broadcast 88 MHz - 108 MHz FM broadcast 270 kHz - 540 kHz the LW and MW areas between LW and AM broadcast 1.6 MHz - 3 MHz the MW area above the AM broadcast band 3 MHz - 6.5 MHz SW 1 6.5 MHz - 14 MHz SW 2 14 MHz - 30 MHz SW 3
The depiction of the AM band has been revised to include the symbols for the two Conelrad frequencies at 640 and 1240 kHz, which were printed on the tuning knobs of radios sold in the United States from 1953 to 1963.
This takes the short-wave range, with wavelengths from 10 metres to 100 metres, and places it on three scales of its own, and these three scales have nearly equal ratios between the high and low frequencies they include.
Some radios with an additional smaller variable capacitor for fine tuning included special markings on the main tuning dial, and had a set of frequency scales on which a frequency was indicated by a pointer showing where the fine-tuning capacitor was set.
This second set of frequency scales could only be used when the main tuning dial was set to the marking corresponding to one of the narrow bands described above. In this case, the fine-tuning feature was called "bandspread", and not only was it important for the main tuning knob to be set in the correct position for one of the bandspread scales to be used, it was also necessary to place the bandspread knob in a starting position for normal tuning, since, to cover an entire small band, it had to modify the tuning to a sufficient extent to materially affect the correspondence between the actual frequency to which the radio was tuned, and the frequency marked on the main dial.
Since only the bands on the main tuning dial were selected by a switch, the frequency range provided by the bandspread feature was not tailored for each individual band. Let us suppose that bandspread is achieved by putting a small variable capacitor in parallel with the main tuning capacitor. This is a common way in which it is done, even when the radio does also have IF stages, being superheterodyne or even dual-conversion or triple-conversion.
As one example of a radio having a bandspread dial, the Realistic DX-200 is studied here. This radio used a rotating barrel with scales placed on it one above the other for each tuning dial; a similar arrangement was used on the Kenwood R-300 and QR-666 radios as well (note that even if the DX-200 was a rebranded Kenwood radio, it was not one of those two models; they did not have the large built-in speaker of the DX-200, but they had several additional features it did not).
Most short-wave radios with bandspread only provided it for the amateur (or "Ham") bands; this one did so for a wide selection of both the amateur bands and the shortwave broadcasting bands.
The frequency bands provided on the basic tuner were:
150 kHz - 400 kHz covering both 150 - 270 kHz LW and other frequencies 520 kHz - 1600 kHz AM radio, of course 1.6 MHz - 4.5 MHz the rest of Medium Wave and the beginning of Short Wave 4.5 MHz - 13 MHz more Short Wave 13 MHz - 30 MHz still more Short Wave
In the three short-wave bands, at the high-frequency end of the various small bands for which bandspread is provided, there were little red dots to which the main tuning knob is set.
Then the bandspread knob is turned away from its "set" position, at the high-frequency (and hence low-capacitance) end of all of its scales, for use as the active tuning knob within those scales.
Because a bandspread capacitor had to be used that would provide a sufficient change of capacitance to cover each of the bands to be spread, in some cases the bandspread scale continued beyond the area of interest, as can be seen from this table:
Band Type Range of bandspread
scale
80 metres A 3.22 - 4.18 MHz
59 metres B 4.83 - 5.13 MHz
49 metres B 5.72 - 6.15 MHz
40 metres A 6.56 - 7.4 MHz
31 metres B 8.25 - 10.1 MHz
25 metres B 9.4 - 12.5 MHz
20 metres A 13.6 - 14.4 MHz
19 metres B 14.6 - 15.5 MHz
16 metres B 16.75 - 18.1 MHz
13 and 15 metres B/B 19.8 - 22.1 MHz
10 and 11 metres A/B 25 - 30 MHz
In a couple of cases, the frequency range for one of the broadcast bands shown above is actually wider than the range shown here for this radio; I believe that this is due to a tendency on my part to accept the wider frequency range from among those given in my sources. For the amateur bands, where my information is more accurate, the band included in the bandspread scale is always wider. And at the high frequency end, there are two cases where the extent of the bandspread scale is wide enough to include two bands at once. Note that the band referred to above as the 60 metre band is designated as the 59 metre band on this radio, which may be more accurate if less traditional.
It may be noted that high frequencies often require not just using small inductances, but also small capacitances, so several radios which had separate bandspread dials also used them as the main tuning dials for the reception of VHF signals, with the ordinary main tuning capacitor simply switched out of the circuit when those bands were selected. The Hallicrafters SX-71 did this for a band extending from 47 to 55 MHz, and the Haynes Super-Clipper is another example of a radio which does this, in its case for several VHF bands.
Incidentally, just as a typical main tuning capacitor for AM radio would be variable from some small value to 365 pF, a typical size for a bandspread capacitor seems to have been 15 pF, although the sources giving examples of that also usually involve a smaller main tuning capacitor; 30 pF is another value used.
The dial given above does not seem to be a realistic example of a radio dial on a shortwave radio, however. One certainly could, as noted above, approximate a straight-line wavelength characteristic for bands having different frequency ratios; for example, a variable capacitor having the following ganged components would offer a wide variety of choices:
170 pF SLW 115 pF " 80 pF " 400 pF SLC 200 pF " 100 pF " 50 pF "
and variable capacitors having nearly this much complexity have been constructed for special purposes. In general, though, a general-coverage short-wave reciever makes do with multiple ganged variable capacitors all the same size, although they might be 200 pF or 150 pF instead of 365 pF.
Let us take the bands given in the example dial pictured above, but let us draw the dial on the basis that a variable capacitor with a range from 365 pF to 14 pF, designed to have a straight-line wavelength character for the AM broadcast band specifically, is the sole variable capacitance element in use, although it will have fixed capacitors placed in parallel with it for bands having narrower frequency ratios than that of the AM broadcast band.
In the following table, we can work out first what size of capacitor (chosen from standard sizes, except in the case of the 582 pF capacitance for the FM band, consisting of a 560 pF capacitor in parallel with a 22 pF capacitor) needs to be placed in parallel with the variable capacitor so that the range of frequencies covered by the band will nearly fill the dial, and then we can choose a suitable inductance value as well. Since this construction, compared to the one above, will supply more correction for the additional crowding of high frequencies on the dial for narrower bands, it may happen that in the case of the band with the smallest frequency ratio, the FM band, which is satisfactory in appearance even when a straight-line capacitance control is used, we will get an unrealistic result which is crowded at the low end of the dial.
Band Ratio of Ratio of Capacitor in Inductance
frequencies capacitances parallel
150 kHz - 270 kHz 1.8 3.24 120 pF 2400 uH
540 kHz - 1600 kHz 2.96296296 8.77914952 15 pF 250 uH
88 MHz - 108 MHz 1.22727273 1.50619835 575 pF 0.0036 uH
270 kHz - 540 kHz 2 4 82 pF 800 uH
1.6 MHz - 3 MHz 1.875 3.51625 100 pF 22 uH
3 MHz - 6.5 MHz 2.16666667 4.69444444 68 pF 6.65 uH
6.5 MHz - 14 MHz 2.15384615 4.63905325 68 pF 1.45 uH
14 MHz - 30 MHz 2.14285714 4.59183673 68 pF 0.31 uH
And here is the dial that results from these choices:
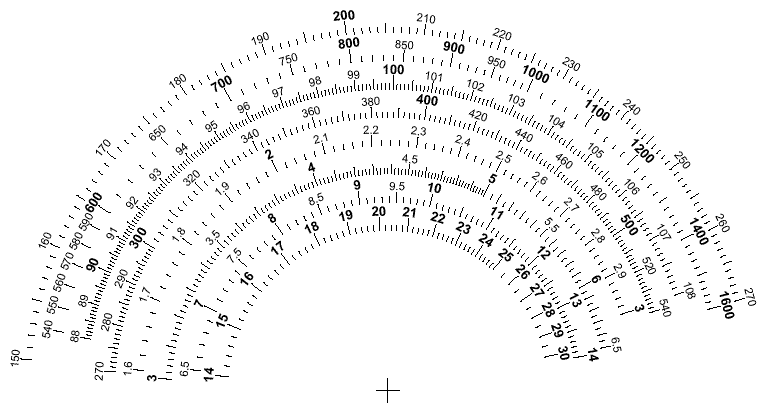
The FM dial does spread out at the higher frequencies, but not by an amount that is a problem, and, thus, the existence of inexpensive AM/FM radios is accounted for. This is a considerably more realistic image of what the dial of a multiband radio might look like.
Terms such as VHF (very high frequency) and short wave have a specific technical meaning, marking major divisions of the electromagnetic spectrum.
3 - 30 Hz ELF extrenely low frequency
30 - 300 Hz SLF super low frequency
300 - 3,000 Hz ULF ultra low frequency
3 - 30 kHz VLF very low frequency
30 - 300 kHz LF LW low frequency long wave
300 - 3,000 kHz MF MW medium frequency medium wave
3 - 30 MHz HF SW high frequency short wave
30 - 300 MHz VHF very high frequency
300 - 3,000 MHz UHF ultra high frequency
3 - 30 GHz SHF super high frequency
30 - 300 GHz EHF extremely high frequency
The designations "long wave", "medium wave", and "short wave", although still in use, are no longer the official designations of the frequency ranges. They are still used to describe specific radio services within those ranges, but they were also the older designations of the frequency ranges as well.
On a related topic, an explanation of how the superheterodyne principle works in radios is present at this location within this site as well.