The photographs on the first page of this document show images formed with a simple glass lens, as found in a magnifying glass. While simple lenses do not form perfect images, the images are often not noticeably imperfect. Thus, we can think of lenses as forming perfect images as a first approximation to the way they actually behave.
Doing so leads to Gaussian optics, or first-order optics. This is the technique used to determine what an optical system formed from a combination of lenses will actually do, or at least attempt to do.
A lens, or a mirror, when considered from the viewpoint of Gaussian optics, has one important parameter, its focal length.
A flat mirror, or a pane of glass, has a focal length of infinity, which leads to it, in effect, not doing anything. Light passes through a flat pane of glass essentially without being redirected. A flat mirror does cause light to move in the opposite direction to that from which it came, but one can ignore that for both flat and curved mirrors, and treat mirrors as if they are lenses, dealing separately with how they fold the optical path.
A convex lens, and a concave mirror, both can be used alone for magnification. These systems both have a positive focal length. A concave lens, and a convex mirror, by itself can only make things look smaller, and they have a negative focal length.
The two rules governing simple lenses are the equations:
1 1 1 --------- + -------- = --- d d f object image
and
d
image
Magnification = ---------
d
object
To apply these rules sensibly, one needs to understand the sign conventions used with them. As noted, a concave lens, also known as a negative lens, has a negative focal length.

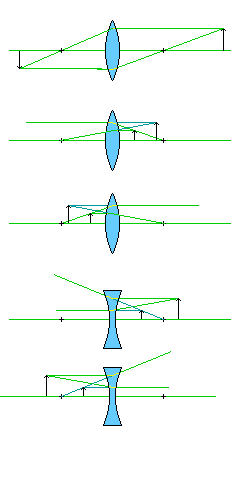
This image, showing the three basic cases of what is known as Gaussian ray tracing, shows us how these equations are used in practice.
A lens is treated as if it is a flat object with no thickness. The fact that a convex lens brings parallel rays of light to a focus at a distance of its focal length from it is used to select two easy-to-draw lines coming from an object which will define where the image of that object is formed.
In the case of a convex lens, one ray comes from a point on the object off the optical axis, and moves parallel to the axis. This ray, then, will be among those brought to a focus at the focal point of the lens on the opposite side.
Another ray is a line passing through that same point on the object, and the focal point of the lens on the same side as the object. So this ray was brought to a focus on this side of the lens, so on the other side of the lens, it will be travelling parallel to the axis.
Where the two rays cross after being bent by the lens, this is where the image of that point on the object will be formed.
A ray passing through the center of the lens will not be bent, and this third possibility can be used whenever one of the preceding two rays is inconvenient to draw.
Thus, in the first of the three diagrams, we see a lens forming what is known as a real image of an object behind the lens: the lens is acting like the lens in a camera, forming an upside-down image which it could be projecting on a screen or on film. The distance from the lens of the object, and of the image, are both greater than the focal length of the lens. Thus, in this case, both distances are treated as positive for the equations above.
In the second diagram, after being bent by the lens, the two rays are spreading apart more quickly than before. So they will not meet on the other side of the lens. Instead, to an observer on that side of the lens, they will seem to come from a point behind the lens, but not the same point as the one at which the object is actually located. The rays leaving the lens are extended by dark green lines, showing where they seem to come from, to illustrate this. Thus, the image is now known as a virtual image, and the lens is behaving like a magnifying glass. So the image distance is considered to be negative; in this way, the difference between the reciprocals of two distances, both smaller than the focal length, can equal the reciprocal of the focal length.
The third diagram looks almost like the second diagram, and illustrates the case where the signs of the two distances are reversed: this is where a convex lens intercepts rays from another convex lens that would form a real image, and bends them so that they form a real image at a different location and of a different size.
The fourth diagram shows how this kind of ray tracing works for a negative lens. In this case, instead of bringing light in parallel rays to a focus, parallel rays are made to diverge as if they are coming from a focus. Here, the difference between the reciprocals of the two distances is negative, as corresponds to the negative focal length of this kind of lens.
The fifth diagram again shows a lens intercepting rays proceeding from another lens which would form a real image, had they not been intercepted. In this case, a negative lens is doing the intercepting, and it is causing the image to end up being formed at a larger size than it would have otherwise been. This is the principle used by a telenegative lens used as a camera accessory, or by a Barlow lens used with a telescope.
Copyright (c) 2001 John J. G. Savard