To see why lenses and mirrors do not actually form perfect images, we need to understand the laws that govern what they actually do.
That light bounces off a mirror at the same angle that it hits it, as summed up in the phrase "angle of reflection equals angle of incidence" is intuitively reasonable (particularly to anyone who has ever played pocket billiards) and hardly bears discussion.
Most of us were also exposed to the law governing refraction in school, but it may bear review. The reason that passage from one transparent medium to another causes light beams to be bent at the surface dividing the two media is because of the fact that dense media normally slow down the speed at which light travels within them.
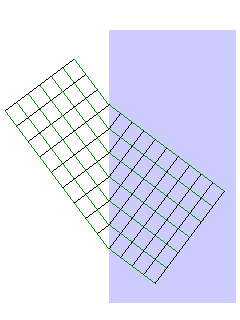
This diagram illustrates how a change in the speed at which light travels can cause light rays to bend.

The rays of light are shown in green; the black lines perpendicular to them represent the peaks and troughs in the light waves of which they are composed. Since those lines are brought closer together when the light travels more slowly, this means that when light enters an area of a different refracive index, they must also change direction, because the waves within the new medium are produced by the waves in the old one, and so the peaks and troughs coincide at the surface.
The refractive index of a medium is the reciprocal of the speed of light in that medium, when that speed is represented as a fraction of the speed at which light travels in a vacuum.
One can see from the diagram with some labelled lengths and angles added:
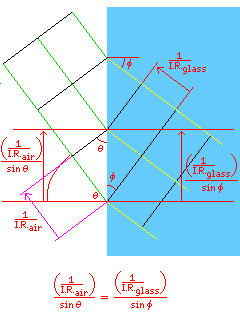
that the distance between successive wavefronts on the surface, which must be equal for both media, is proportional to the reciprocal of the refractive index of the medium, and to the reciprocal of the sine of the angle of incidence from that medium.
Thus, Snell's law is:
sine(angle of incidence 1) * (refractive index 1) = sine(angle of incidence 2) * (refractive index 2)
There is a handy geometrical construction, due to the British physicist Thomas Young, after whom Young's modulus, a measure of how stiff a spring is, is named, for determining the path of light rays passing through a spherical (or cylindrical) surface.
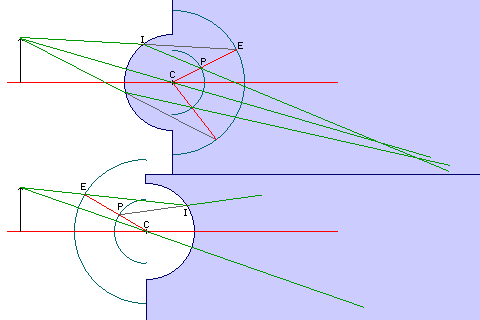
In addition to a circular arc representing the surface in question, one makes arcs on the opposite side of the same center, one enlarged by a factor corresponding to the index of refraction of the medium one is entering, and one reduced by that same factor.
Given the form that Snell's law takes, in the case where two glasses are involved, one uses the ratio of the two refractive indices, and the roles of the circles are reversed when leaving a medium.
The path the ray of light would take if the medium were not present intersects the big circle at the point E; a line between E and the center of the circles C crosses the smaller circle at the point P, and a line between the point at which the ray of light hits the surface at which it is refracted, I, and that point P, gives the direction in which the ray will continue after being refracted.
The diagram illustrates the two possible cases. This geometrical construction gives the actual way the rays will be bent according to Snell's law, rather than the first-order Gaussian optics approximation.
While today ray tracing is done by computers, it is still interesting to know that such a construction existed.
Copyright (c) 2001 John J. G. Savard