Having seen the basic laws that govern how lenses and mirrors work, now we will examine some ways in which one of the basic aberrations of lens and mirror systems, spherical aberration, can be eliminated in a mathematically exact fashion.
In the case of mirrors, it can be shown from geometry that a parabolic mirror reflects parallel rays of light towards its focus, an elliptical mirror reflects rays coming from one of its foci to the other focus, and a hyperbolic mirror reflects rays of light aimed at the focus behind the mirror to the focus in front of the mirror. These are the curves which eliminate spherical aberration when used with mirrors. However, they do not eliminate other limitations of optical systems, such as coma, as was noted when the Ritchey-Chrètien telescope design was discussed.
Of course, the Newtonian telescope design, for example, is still quite useful, even if it has some coma, and other aberrations. Every lens and every mirror results in the loss of some light, and so a Newtonian, particularly one with a long focal ratio, represents a very good compromise between the correction of aberrations on the one hand, and preserving as much as possible of the incoming starlight.
It is not nearly so obvious what the equation might be for the ideal shape of a lens that focuses parallel, on-axis rays to a single point, thus eliminating spherical aberration.
This diagram illustrates, though, that there is one way to construct a lens with spherical surfaces that is totally free of spherical aberration.

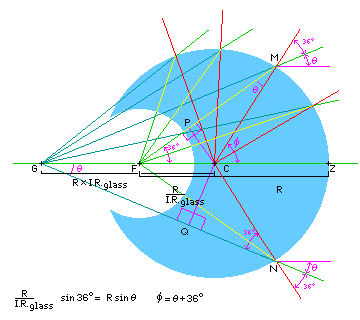
This diagram illustrates what are known as the aplanatic points of a sphere. A sphere of glass can bring light that is heading to a focus behind it to a focus at a point within it, with freedom from two aberrations, spherical aberration and coma. This is why the points are called aplanatic points, because a lens corrected for those two aberrations is called an aplanat. To allow the focus within the sphere to be useful, in the diagram I have taken a spherical bite out of the sphere of glass, with its center at this focus. This means light from that focus hits the edge of that spherical bite perpendicularly everywhere, avoiding at least spherical aberration at that surface. (An encyclopedia article claims that the center point also avoids coma, so the lens remains aplanatic: spherical symmetry certainly is a way to avoid coma, as in the original Schmidt and Maksutov designs, but when the image is at the center of the sphere, it's not clear if mathematical freedom from coma means anything useful.)
As the diagram attempts to illustrate, when a ray of light comes from that focus, and is eventually refracted at the outer edge of the sphere of glass, a triangle is formed.
The point the light comes from is located at a distance from the center of the sphere equal to the radius of the sphere divided by the index of refraction of the glass from which it is made.
Because of that, the triangle can be divided into two right triangles, and the sides of those right triangles that lie along the path of the beam of light are also in the ratio of the index of refraction of the glass. Thus, because these two triangles also share a side, the sines of the angles at the point from which the light came, and the point at which it encountered the surface of the sphere, are in that ratio as well; and this is also the ratio given by Snell's law.
Thus, the light after refraction appears to come from a point whose distance from the center of the sphere is equal to the radius of the sphere times the index of refraction of its glass, since the apparent path of that light forms a triangle which is similar to the triangle formed by the actual path of the light within the glass, except that it is larger, and flipped over.
More fully:
From the point F, located so that the length of the line segment FC is one over the index of refraction of the glass from which the sphere is made times the radius of the sphere (also the length of line segment CZ), the diagram shows several equally-spaced rays of light proceeding outwards, at angles of 18, 36, 54, and 72 degrees.
Taking, as an example, the line radiating out at 36 degrees, we follow it to the point M at which it leaves the sphere. (Note that the point F is surrounded by a spherical hollow in the glass sphere centered on it. Since all rays of light leaving F strike the surface of that hollow directly normal to it, they are not refracted, and the hollow can be ignored. It is shown to illustrate how a useful lens can be built using the aplanatic point of a sphere despite the fact that it lies within the glass.) Let us call the angle this ray of light makes with the normal to the sphere at that point theta.
Note that the length of FC is equal to the length of MC divided by the refractive index of the glass.
Observe point P. Point P is the point on line segment MF at which a line perpendicular to MF intersects the point C, the center of the sphere. Thus, angles MPC and FPC are both right angles.
Thus, the length of line segment PC is equal to the sine of 36 degrees times the length of line segment FC, which is the radius of the sphere divided by the index of refraction of the glass. The length of the line segment PC is also equal to the sine of theta times the length of line segment MC, which is the radius of the sphere. Hence, the sine of theta equals the sine of 36 degrees, divided by the refractive index of the glass.
This means that theta, the angle the ray makes with the normal to the sphere, is precisely the right angle within the glass to produce, outside the glass, an angle of 36 degrees to the normal, as a result of Snell's Law. The difference in length between line segments FC and MC is such as to produce an opposite effect exactly matching that of Snell's Law, which is the key to the importance of the point F. Thus, the ray of light, which at point M makes an angle of theta with the normal to the sphere within the sphere, will leave the sphere making an angle of 36 degrees with the normal to the sphere.
Let G be the point on the optical axis from which the ray of light appears to come. Looking at point N, which is the point opposite to M by reflection about the optical axis, we now wish to determine where G is located. (Our goal is to show that G is independent of the angle of 36 degrees at which our ray started, to show that our spherical lens is free from spherical aberration.)
Angle MFC is 36 degrees, and angle FMC is theta. Therefore, as the angles of a triangle add to 180 degrees, angle FCM is 180 - ( 36 + theta ). Hence, angle MCZ, which we denote as phi, is equal to theta plus 36 degrees. This means that the ray of light leaving the sphere, which makes an angle of 36 degrees with the normal to the sphere, also makes an angle of theta with the horizontal (and, hence, the optical axis).
Hence, returning to the lower half of the diagram, angle GNC is 36 degrees, since that is the angle the ray of light makes to the normal to the sphere on exit, and line segment NG continues the path of the ray of light leaving the sphere, showing where it appears to come from, the image point.
Because this ray of light makes an angle of theta with the optical axis, angle NGC is theta as well.
Hence, triangle MCF and triangle GCN are similar triangles, and the lengths of the sides MC and FC of triangle MCF have lengths in the same ratio as sides GC and NC of triangle GCN. Thus, the length of line segment GC must be the radius of the sphere times the refractive index of the glass.
For illustrative purposes, the spherical bite out of the large sphere is a small one. Lenses with a larger bite of this type, and more than one of them in sequence, are often found in microscope objectives. Sometimes, instead of a spherical bite surrounding the aplanatic point, a lens is used that is simply half of a sphere; this is used in an oil immersion microscope, where the specimen is placed in a liquid, which the lens touches, having the same refractive index as the glass of the lens, thus, in effect, putting the specimen inside the glass.
Note that this diagram is drawn to scale for a refractive index of 1.52, which is a typical value for normal crown glass.
Copyright (c) 2001 John J. G. Savard