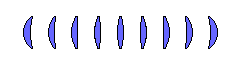
There are seven basic aberrations that are normally of concern in optical systems.
Two of these aberrations have to do with the properties of glass, and can be understood in terms of first-order or Gaussian optics. These are the two forms of chromatic aberration. Unfortunately for lens designers, glasses do not slow down all forms of light by the same amount. Instead, blue light, with a shorter wavelength, is slowed down more than red light, so the glass has a higher index of refraction for blue light than for red.
There are two forms of chromatic aberration, axial (or longitudinal) chromatic aberration and lateral (or transverse) chromatic aberration. An optical system made from only one kind of glass can be designed so that images of different colors remain in focus, thereby correcting for axial chromatic aberration, by having spaced elements such that a proportional decrease, or increase, in the focal length of each element will cause the image formed by one element to move in the same direction as the focal point of the next element. The Huyghenian eyepiece is designed to take advantage of this principle.
Since an intermediate image is now formed at a different distance from the two lenses, however, the magnification of the system will change, and thus longitudinal chromatic aberration is not corrected, and so the two are viewed as separate aberrations.
Since we are beginning the study of aberration, one thing we will need to know is what shape a lens, or, for that matter, a mirror, of a given focal length will have.
The focal length of a curved mirror can be determined from the locations of its two foci; thus, a parabola has its one focus at its focal point, so the distance from its base to the focus is its focal length (the parabola with the equation y=x^2 has its focal point at x=0, y=1/4); a sphere takes an object at its center and produces an image at its center, and thus 1/f equals 1/r plus 1/r, so its focal length must be half its radius.
A lens with one flat surface, and one curved surface of radius r has a focal length of r/(N-1), where N is the index of refraction of the material the lens is made of (divided by the refractive index of the surrounding medium).
When the focal length of a lens is measured in meters, the reciprocal of that focal length is the power of the lens, measured in diopters.
This is important because when two lenses are very close together, one can just add their power together to get the power of the combination.
This is useful for two things. One of them is to determine the focal length of a lens when both of its sides are curved. Choosing between a double convex lens, a planoconvex lens, or a meniscus lens in an optical design is an important method of controlling spherical aberration, coma, and the other three Seidel aberrations which we will meet in the next section. Another is to determine how to abolish both kinds of chromatic aberration at once by using two lenses in close contact made from two different kinds of glass, so that their total power is the same, at least for two wavelengths of light. The lens formed by two elements of this sort is called an achromatic doublet, or an achromat.
The two most common kinds of glass used for making achromats are crown glass and flint glass. Crown glass is similar to ordinary window glass, but made more carefully. Flint glass is similar to lead crystal, because its greater dispersion and index of refraction is obtained from including lead oxide in the glass, just as it adds sparkle to crystal.
Crystal glass is divided into different categories based on its proportion of lead oxide:
17% Crystal 24% Lead Crystal 30% Full Crystal
Dense flint glasses can have a proportion of lead oxide as high as 65%. 24% lead crystal has a refractive index of 1.56, and thus has properties similar to optical glass in the Light Flint category.
This diagram illustrates several lenses having different shapes, but the same power.
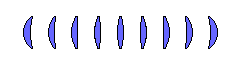
Changing from one form such as those shown above to another is called "bending" the lens.
One way in which an achromat is constructed is to select two lenses whose total power is the same for a particular kind of red light and blue light. While such a lens will not bring the colors of light in between to the same focus, this still will be a reasonable way to reduce chromatic aberration for the whole spectrum, for the simple case when only two lenses and two kinds of glass are used. The focal length of the lens as a whole, however, will still be determined using light in the middle of the spectrum. The yellow-green light of the sodium D line was originally used for that purpose; since that spectral line is really formed by two closely-spaced wavelengths of lights combined, for greater accuracy the current standard for this purpose is a spectral line of a similar color produced by helium.
Two numbers describing a type of glass are sufficient for designing a simple achromat in this way. One is the refractive index of the lens in yellow-green light, noted as N or N sub D (or N sub d nowadays). To ensure that the red and blue light are both brought to the same focus, one needs to know the difference between the refractive indices of the glass for the two wavelengths, so that the difference in the powers of each lens component for the two wavelengths can be made to cancel out. To allow calculations to be performed directly on the basis of the power of each lens component, without having to work out the curvature, this difference is scaled to the refractive index of the lens in the yellow-green light, minus one (since, as we saw, power is proportional to refractive index minus one). Then the reciprocal is taken, to facilitate working with focal length instead of power. The result,
N - 1
D
-------------
N - N
F C
where N sub F is the refractive index for the blue light, and N sub C is the refractive index of the red light, is called the dispersion of the glass, and is usually noted by the Greek letter nu, subscripted with D (or d, as the case may be).
Representing N sub d by N, and nu sub d by V, for each of two kinds of glass (N1, V1, and N2, V2) we can now express the equation for an achromat with focal length f:
the power of each lens is given by:
P1 = 1/F1 = C1 * (N1 - 1) P2 = 1/F2 = C2 * (N2 - 1)
(C stands for curvature, one over the radius of a surface; here, the curvature of a lens is the sum of the curvatures of its two sides, since that adds the powers of its two sides) and the difference between the powers of each lens for the blue and red light are given by:
D1 = C1 * (NF1 - NC1) = P1/V1 D2 = C2 * (NF2 - NC2) = P2/V2
and our goal is to solve for:
P1 + P2 = 1/F1 + 1/F2 = 1/F D1 + D2 = P1/V1 + P2/V2 = 1/(F1 * V1) + 1/(F2 * V2) = 0
The second equation can be further simplified: the two lenses need to have powers of opposite types, and the ratio of their focal lengths (except for the sign) is to be the reciprocal of the ratio of their dispersions.
To take an example, let us say we wish to construct an achromatic telescope objective with a focal length of 1.44 meters (approximately six feet) from two kinds of glass. For simplicity, instead of taking the parameters of real glasses, I will take values that are rounded off to typical values:
Crown: N = 1.52, V = 59 Flint: N = 1.6, V = 38
From the second equation, we can see that if the crown element had a focal length of 38, and the flint element was a concave lens with a focal length of -59, we would have an achromatic lens.
The focal length of the result would be 1/((1/38)-(1/59)), or 106.7619.
To obtain any desired focal length, we need merely change all the focal lengths involved by the same ratio. So, 1440/106.7619 equals 13.48796, by which we can multiply 38 and 59 to get the focal lengths of those components in millimeters: the crown element should have a focal length of 512.5 mm, and the flint element should have a focal length of -795.8 mm.
We could use N to work out possible curvatures for these elements. There are, however, many possible choices. Since flint glass is softer than crown glass, usually the crown element will be the one facing the outside of the telescope.
As we've seen, f = r/(N-1), or p = (N-1)c = 1/f. And the powers of the two sides of the lens add. Let's suppose we will make the crown element of the lens perfectly symmetric, like a magnifying glass. This simplifies handling the lens once made, and is close to one design with reduced aberration.
Then, each side will have a radius of curvature equal to 1025 * .52, or 533 mm.
One side of the flint element will have a curvature matching that of the crown element. This allows the two elements to be cemented together, which saves on applying antireflection coatings to two surfaces. The desired power of the flint lens is -1.2566 diopters. Since p = (N-1)/r, the power supplied by the one surface of the flint lens that we've determined is -.6/.7958 diopters, or -.7540 diopters. So the other surface has to be convex, to supply some positive power.
The answer works out to a radius of 837.7 mm for the back surface of the flint element.
Despite the fact that flint glass has a higher index of refraction than crown glass as well as greater dispersion, because the dispersion increases more quickly, different glasses do complement each other well for the purpose of bringing two colors together in an achromatic lens.
But if one tries to bring three colors together by using three different types of glass, the picture is not quite as positive. Most types of glass share a common behavior, known as lying on the glass line, that makes it difficult to cancel out three colors with ordinary glasses. Some common substances, however, are potentially useful for correcting a third color. Clear plastics, particularly acrylic and polycarbonate, lie off the glass line in one direction (acrylic is the "crown" glass of plastics, and polycarbonate the "flint"), and water lies off the glass line in the other. At one time, astronomers actually experimented with lenses that included an element formed from water lying between two glass lenses.
In general, though, while plastic is certainly cheap, it has to be processed in a different way from glass, it is also somewhat less transparent, and, perhaps most serious of all, it is affected by changes in temperature about a hundred times as much as glass.
However, there is a workaround for this last flaw. A lens can be designed so that those of its elements which provide the power of the lens are made from glass, so that the focal length of the lens is stable, but other elements whose combined effect is afocal, and whose purpose is to correct aberrations, are made from plastic. This principle was illustrated in U. S. Patent 2,406,762, by D. S. Grey for the Polaroid Corporation, in which it is further noted that, since the effects on both the glass and the plastic of temperature are in the same direction, giving the plastic elements a small net power in the opposite direction from that of the glass would more thorougly protect the lens from changes in temperature.
Thus, the large, heavy meniscus elements in a double-Gauss camera lens might be made from plastic.
Fluorite (calcium difluorite) lies considerably further from the glass line than plastics, and it was the material used in the first apochromatic lenses, microscope objectives designed by Ernst Abbé at the Zeiss optical firm. There are now glasses that have optical properties similar to that of fluorite, but they too are expensive and sensitive to damage from humidity and other environmental factors. Fluorite, in addition to being used in the objective lenses of more expensive refractors, is of course well known for its use in high-quality camera lenses as well.
Also, newer glasses are available that function like crown glass, but with considerably less dispersion to cancel out. Such lenses are often made by including the oxides of Barium or Lanthanum in the glass. Barium glasses were the first such glasses to be made, and their discovery made it possible to design lenses which were corrected for curvature of field. Some barium glasses are reasonably inexpensive as optical glass, and they are often found in the lens elements of binoculars, for example.
Glasses including Lanthanum are of more recent vintage, and they are fairly recent; telescope objectives using such glass can have a level of chromatic aberration comparable to that of apochromatic lenses.
For a crown glass, a flint glass, acrylic plastic, and polycarbonate plastic, we have:
BK 7 F 2 Acrylic Polycarbonate
n 1.51432 1.61503 1.4892 1.583
C
n 1.51680 1.62004 1.4918 1.590
d
n 1.52238 1.63208 1.4978 1.601
F
n - 1
d
------- 64.17 36.37 57.4 31
n - n
F C
With BK7 and F2 as the crown and flint glasses, we can use the number (nF-nC)/(nd-1) directly (or its reciprocal, the more common Abbe number) to find out the ratio of the powers (for the light of the middle line, called "d") of the two components in an achromatic lens. If we just use nF-nC without dividing by nd, instead of the ratio of the powers of the lenses, we would have the ratio of their "thicknesses"; not thickness as in a distance, but simply the power of the lens as indicated by its shape without reference to the refracting power of the substance from which it is made.
What we would find with nF-nC for two glasses and two wavelengths, we can find for three glasses and three wavelengths through straightforward matrix inversion, or a little algebra. Or, we can state the result directly in terms of the powers of the lenses under the Helium d line (replacing the old standard of the Sodium D line because that line is really two spectral lines close together, making it less precise) by using (nF-nC)/nd to construct two achromats with two pairs of glasses from these three, and then using (nF-nd)/nd to combine the two mixtures.
Thus, we find that a BK7/F2 achromat, with a focusing power of 1 diopter in helium-d light, is composed of a positive BK7 component with a focusing power of 2.3083 diopters and a negative F2 component with a negative power of 1.3083 diopters and the focusing power of this lens in hydrogen-C and hydrogen-F light is about 0.99951 diopters.
Similarly, with an acrylic/F2 achromat, a power of 1 diopter is attained with powers of 2.7294 diopters and 1.7294 diopters for the respective components, and a focusing power in hydrogen-C and hydrogen-F light of about 0.99963 diopters.
Thus, as the deficit of the acrylic/F2 achromat is as 37 to a deficit for the BK7/F2 achromat of 49, if we take the acrylic/F2 achromat as the starting point, and subtract a BK7/F2 achromat of 37/49ths the power, we obtain an apochromat. Thus, both the crown and flint lenses are negative, while the acrylic lens is positive.
If we started with an acrylic/F2 achromat with a power of 1 diopter, the result would have a power of 12/49ths of a diopter, so we can multiply by 49/12 to scale up to obtain the required lens design:
Power of acrylic component: (49/12)*2.7294 = 11.145 diopters (converging) Power of BK7 component: (49/12)*(37/49)*2.3083 = 7.117 diopters (diverging) Power of F2 component: (49/12)*(1.7294-(37/49)*1.3083) = 3.028 diopters (diverging)
Thus, an apochromat with these three materials will have to have a slow focal ratio, so as to avoid overly steep curves. Since some camera lenses are made with plastic components to save cost and weight, it is not impossible that someday an apochromatic telescope with a plastic component might be offered for sale to the public.
One of the problems with using plastic lenses in a telescope, however, is that the properties of plastics change much more rapidly with temperature than those of glass.
If we began the design of a telescope objective with a plastic component by including an acrylic element and a polycarbonate element of equal and opposite powers, then, based on the figures above (which are only approximate at this time for polycarbonate) as measured in helium-d light, with the polycarbonate element negative, then if each of those elements has a power of 1 diopter at that wavelength, the combination has a focusing power of 0.00423 diopters in hydrogen-C light, and one of -0.004605 diopters in hydrogen-F light.
We would wish to combine this with a glass lens with crown and flint components that is undercorrected for chromatic aberration if possible. If not, we would need to use one that is overcorrected, and make the polycarbonate element positive and the acrylic element negative.
One simple way to solve the system of equations involved would be to see how this compound plastic lens could be combined with lenses of the flint and crown types being considered to create an achromatic lens.
An F2 lens with a converging power of about 0.8395 diopters in Helium-d light would, when combined with this compound plastic lens, produce an achromat with a converging power of about 0.8411 diopters in Hydrogen-C light and Hydrogen-F light, .0016 diopters more.
A BK7 lens with a converging power of about 1.3837 diopters in Helium-d light would, when combined with this compound plastic lens, produce an achromat with a converging power of about 1.3842 diopters in Hydrogen-C light and Hydrogen-F light, .0005 diopters more.
So we can combine these two lenses in the proportions 16/11 parts BK7 and -5/11 parts F2 to obtain an apochromat consisting of:
These figures are based on a rough calculation, it should be noted. If one were going to try experimenting with such a lens through the purchase of standard off-the-shelf lens components, one way to do this would be to start with a BK7/F2 achromat; let us assume that it has a focal length of 800mm. Then the F2 component would be a diverging lens with a focal length of 611.5mm, and its BK7 component would be a converging lens with a focal length of 346.6mm.
Since we want the BK7 components of this system to have a combined focal length of 115.6mm to be about 5.29 times as powerful as the F2 component, we would want to add a plain BK7 converging lens with a focal length of 173.47mm.
And the acrylic lens and the polycarbonate lens would both have focal lengths of 232.5mm.
Copyright (c) 2002, 2004, 2009 John J. G. Savard