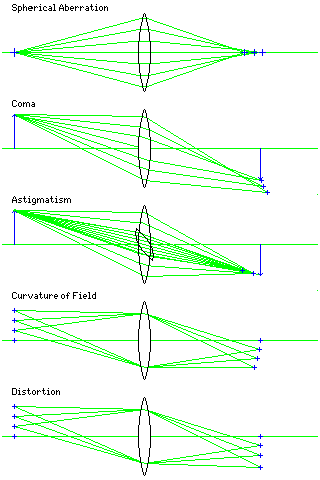
The five basic types of aberration which are due to the geometry of lenses or mirrors, and which are applicable to systems dealing with monochromatic light, are known as Seidel aberrations, from an 1857 paper by Philipp Ludwig von Seidel. These are the aberrations that become evident in third-order optics, also known as Seidel optics.
As we know,
3 5 7 9 11 13
x x x x x x
sin(x) = x - -- + -- - -- + -- - --- + --- - ...
3! 5! 7! 9! 11! 13!
and
2 4 6 8 10 12
x x x x x x
cos(x) = 1 - -- + -- - -- + -- - --- + --- - ...
2! 4! 6! 8! 10! 12!
When we neglect the later terms in the series, so that we behave as if sin(x) = x, and cos(x) = 1, we obtain first-order optics, in which all lenses are perfect. When we include the x squared and x cubed terms, then we have proceeded to third-order optics, in which the aberrations resulting from the nature of real lenses, exclusive of chromatic aberration, become evident.
The five Seidel aberrations are:
The following diagram attempts to illustrate these aberrations:

Since we know the exact laws which govern the operation of lenses and mirrors, it is possible to determine the exact course of light through any optical system by means of ray tracing. At one time, this was a very laborious procedure, but now it can be carried out automatically by computers, and, as well, computers are no longer expensive.
However, simply choosing optical designs at random, and then finding out whether or not they work is not likely to get one anywhere fast. Instead, one needs a sense of what kind lenses will work together in a design to compensate for each other's aberrations. Knowledge of a large number of existing optical designs is one way to address this difficulty. Third-order optics, because it breaks down the aberrations of lenses into five quantities that can be manipulated arithmetically, also plays a considerable role in finding a starting point for a new optical design.
The two kinds of chromatic aberration bring the total to seven. There are also higher-order aberrations. Sometimes, it is so important to combat chromatic aberration, that one tries to suppress the secondary spectrum left over from an achromatic lens that brings two wavelengths together, and using three kinds of glass, bring three wavelengths together to create an apochromat. Also, given that there is chromatic aberration, a lens system with two kinds of glass, designed to correct the five Seidel aberrations for one wavelength of light will, even if built out of closely spaced achromats, still have these aberrations for other wavelengths; thus, the chromatic variation in the aberrations is another higher-order consideration. As well, going to higher-order terms in the expansion of the sine and cosine functions leads to an additional set of nine aberrations at the next step.
Usually, except for designing an apochromat, it isn't helpful to think in terms of the higher-order aberrations directly; their effects were minimized through actual ray-tracing even in the days when the calculations for it were done by hand. (Some optical design programs do actually improve their performance by calculating fifth-order and seventh-order aberrations as well; the classic book Optical Aberration Coefficients by Buchdahl, available from Dover Publications, gives these formulas explicitly.)
To get rid of aberration in optical design, understanding it in terms of the five Seidel aberrations is helpful. We need two things to benefit from this help. We need a simple formula for the aberrations a spherical refracting surface will cause. The formula can be approximate, as long as it gives us the right answer for when the aberrations become small. And we need a way to combine the aberrations from multiple lenses.
It turns out this is possible. One reason for that is that multiplication can sometimes be approximated by addition. So if a and b are both much smaller than one, (1+a) times (1+b), which is (1+a+b+ab), is approximately 1+a+b. So, if a and b are thought of as deviations from perfection (multiplying by 1) the deviations can be treated as simply adding even when multiplication is the correct rule. Another is that distorted images do pass through successive lenses in a simple way. This is particularly obvious in the case of the aberration of distortion: an image with only that aberration is still an image in focus on a flat plane, so it would be magnified the same way the original object would be by successive lenses. In the case of other aberrations, one optical law is the key to following them through an optical system.
If a lens magnifies an object N times, (small) front-to-back distances in the object are magnified N squared times.
This gives us a rule by which we can scale longitudinal aberrations of any lens in an optical system, to determine their contribution to the aberration of the system as a whole. Transverse aberrations, of course, simply scale by the magnification of the image.
It may also be noted that until quite recently, it was hard to find books in English dealing with optics which went beyond first-order Gaussian optics when dealing with how lenses work. In German, on the other hand, there was a considerable literature on optical design.
However, this began to be remedied to at least a limited extent at a somewhat early date. Important early advanced works on optical design are:
The Optics of Photography and Photographic Lenses, J. Traill Taylor; 1892. A third edition with revisions and additions was published in 1904.
Contributions to Photographic Optics, Otto Lummer, as translated by Silvanus P. Thompson; 1900. The translator added a full explanation of Seidel third-order theory in an appendix.
Application of the Algebraic Aberration Equations to Optical Design, I. C. Gardner; 1927. This was a publication of the U. S. Government, specifically the Bureau of Standards.
Applied Optics and Optical Design, Part One, A. E. Conrady; 1929. Dr. Conrady intended there to be a second part to this work, but he passed away before it could be completed. Rudolf Kingslake, himself a noted figure in optics, and Dr. Conrady's son-in-law, completed the work, making use of materials and notes left behind by Dr. Conrady, and so Part Two of the work was published in 1960.
Optical Design, MIL-HDBK-141; 1962. This is the famous Frankford Arsenal optical design handbook.
Copyright (c) 2001, 2004, 2024 John J. G. Savard