One of the things commonly believed about Einstein's Theory of Special Relativity is that it says that it is impossible to go faster than the speed of light.
I would say that this belief is true, subject to some qualifications.
Special Relativity has been proven to be true by countless experimental tests. And so its predictions, such as Lorentz contraction, and time dilation, and the increase of mass with speed, are known to be true. And, therefore, if you try to go faster than the speed of light by building a faster rocket ship, as its speed approaches the speed of light, it keeps getting heavier without limit. So going faster than light by ordinary mechanical means is indeed proven impossible.
But Special Relativity makes a more ambitious claim about speeds faster than light. It claims that any kind of travel or even just communication faster than light is completely impossible.
Normal matter can interact with light, which is why we have both light bulbs and cameras. It has been postulated that if particles that had an imaginary rest mass existed, not only could those particles move faster than light, but they could never do anything else. If light interacts with matter, it should also be able to interact with tachyons.
And tachyons at least obey the equations of Special Relativity. But Special Relativity claims we will never be able to build a tachyon radio, on the basis of the argument I will shortly present.
Physical theories, however, aren't like mathematical theorems. The argument we are about to look at depends on the FTL communications device or space drive obeying the rules of Special Relativity. The Special Theory of Relativity may say what can't happen if it is correct, but not what can't happen if it's wrong. Although it's been proven to be true as far as all the physical phenomena we know about are concerned, if the FTL device which we haven't seen yet doesn't obey Special Relativity, then there would be no problem.
Thus, if a spaceship travels faster than light by leaving our universe, and going to another dimension where infinite speeds are allowed, and then returning to our universe after doing its travelling in there, then there is no problem. You can't pick up another universe and make it move, and so this other universe would determine a fixed inertial reference frame from which all faster-than-light trips also appear to be forwards in time.
Thus, the maxim is: "Relativity, causality, FTL: pick any two". We're about to see why this is the case; why, if an FTL drive were completely obedient to the rules of Special Relativity, it would allow you to travel backwards in time.
Incidentally, many scientists will drop that qualification, and just state that FTL travel and communication is flatly impossible. There is a simple reason for that.
Special Relativity shows us how nature bends itself out of shape in order to ensure that the speed of light is the same in all reference frames, so that the laws of physics, including Maxwell's Equations, which determine the speed at which electromagnetic radiation (including light) propagates, are the same in all reference frames.
So it would seem oddly strange and perverse for us to live in a Universe that has physical laws that are oriented around Special Relativity... and which then makes a special exception to those laws just so that faster-than-light travel is possible!
This is a reasonable enough point of view. Still, one shouldn't set conditions on what Nature can do. The EPR paradox, concerning the behavior of entangled particles, shows that Nature seems to have a system of faster-than-light communications between entangled particles in order that it can keep its books balanced.
So, perhaps, if someday we were to discover a way to travel or communicate faster than light, we would also at that time discover a good reason for that being possible so that its possibility would no longer seem perverse.
But in the real world, that is not the way to bet. Despite our hopes and so much enjoyable science fiction, we should indeed resign ourselves to the sad fact that faster-than-light travel almost certainly will never be possible.
Of course, at the moment, NASA has bolder spirits working for it, and it is investigating within its Advanced Propulsion Physics program whether faster-than-light travel by means of the Alcubierre Drive might actually be realized. Given the history of aviation, which included "proofs" that heavier-than-air flight is impossible, and indeed that the bumblebee can't possibly fly, this viewpoint of empirical optimism is also understandable.
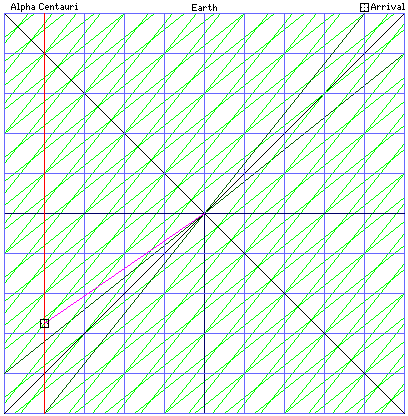
First, let us imagine someone invents a space drive that allows a spaceship to travel at four times the speed of light.
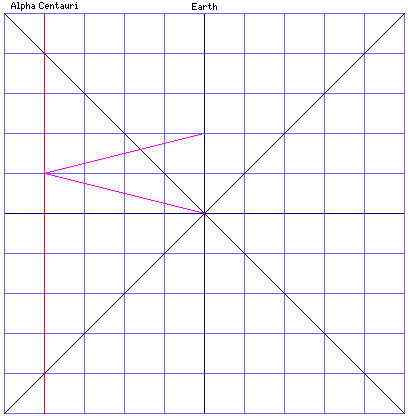
So the ship leaves Earth at a certain time, arrives at Alpha Centauri one year later, and then returns to Earth two years later.
No problem, right?
Note that, to keep things simple, I'm assuming that Alpha Centauri is exactly four light-years away from the Earth, and that it is not moving relative to the Earth. Neither of these things are quite true, but they're close enough.
Also notice that in this chart, each horizontal division represents one light-year, and each vertical division represents one year. The two black lines that form an X show two beams of light travelling past the Earth in opposite directions, dividing the Universe up into "timelike" and "spacelike" areas from when the FTL ship began its journey.
The red line represents Alpha Centauri, and the purple line represents the FTL spaceship.
As it happens, this FTL space drive obeys the rule of Special Relativity that says the laws of physics are the same in all reference frames. So someone has the bright idea of getting to Alpha Centauri even faster, by launching the FTL spaceship from a space platform that is travelling towards Alpha Centauri at 80% of the speed of light!
What happens?
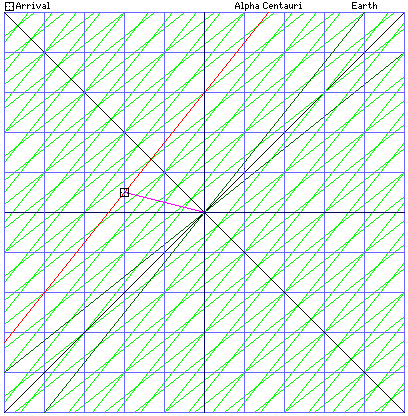
First, we'll look at a Minkowski diagram that shows how things look from the viewpoint of the moving space station. So in this diagram, the blue lines which form a regular Cartesian grid show the x-axis as horizontal, the time axis as vertical, from the viewpoint of the space station. The green lines show the coordinate system from Earth's viewpoint, as that system is distorted from the space station's point of view.
Because of the Lorentz contraction, now Alpha Centauri isn't just heading towards the space station at 80% of the speed of light, it started out as being only 2.4 light-years away, instead of four light-years away!
And so, in six months, Alpha Centauri is 2 light years away, and the spaceship travelling at four times the speed of light arrives there! Obviously, the experiment was crowned with success!
Or was it? How do things look from the viewpoint of Earth - and Alpha Centauri?
To figure out how things look in different reference frames, we have to use the Lorentz transform, which we met on the previous page, of course:
x' + vt'
x = ------------------
__________
/ 2
/ v
/ 1 - ----
/ 2
\/ c
y = y'
z = z'
vx'
t' + ----
2
c
t = ------------------
__________
/ 2
/ v
/ 1 - ----
/ 2
\/ c
Since we're dealing with a speed of 80% of the speed of light, v/c squared is 0.64; one minus 0.64 is 0.36, and the square root of that is 0.6.
What we wish to transform is the time and place of the spaceship's arrival at Alpha Centauri. In the moving reference frame of the space platform, the time of its arrival, t', is 0.5, and the position of its arrival along the x axis, the line going through Earth (or, more properly, the Sun) and Alpha Centauri is -2.
Since it is at Alpha Centauri that the spaceship arrived, we know that x will be -4 without even using the Lorentz transform, but we can still use it to check that we're doing our calculations correctly.
Incidentally, since the moving space platform was going towards Alpha Centauri, thus moving to the left on our diagram, v is equal to -0.8c.
So: x equals -2 plus -0.8 times 0.5, all divided by 0.6. That's -2.4 divided by 0.6, which equals -4, just as we expected.
Now to calculate t. (It's possible, from the Minkowski diagram of how things look from the space platform, to solve for it graphically, by counting the green lines, but I won't spoil the surprise.)
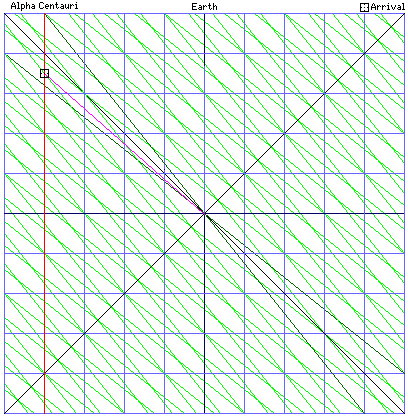
t' is 0.5, v/c is -0.8, and x'/c is -2 (x' is -2 light years, so x'/c is -2 years). So t is 0.5 plus 1.6, all divided by 0.6. That's 2.1 divided by 0.6, or 3.5. Which is exactly what can be seen by graphical methods as well. And so we get the result that is shown on the diagram to the left, which shows the situation as it looks from the reference frame shared by Earth and Alpha Centauri. So in this diagram, the blue lines represent the coordinate system of that frame, and the green lines represent the coordinate system of the space station.
So the spaceship took three and a half years to get to Alpha Centauri, just going barely faster than the speed of light! How can this be?
For velocities slower than that of light, if you add some more velocity to an existing velocity that is already close to the speed of light, the change is less than you would expect, going to zero when the speed of light is reached.
So in a way, it sort of makes sense that the amount of velocity added goes negative after you pass the speed of light.
All right, then, so we go back to the drawing board. What happens if we launch our spaceship, going at four times the speed of light, towards Alpha Centauri from a space platform going away from Alpha Centauri at 80% of the speed of light?
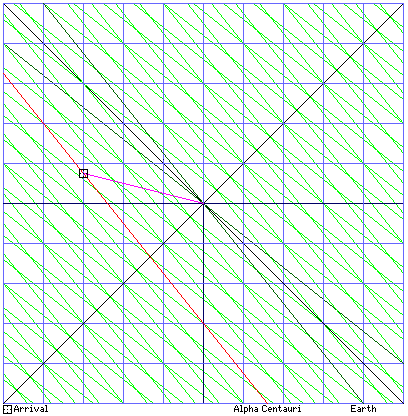
Once again, we'll start with how things look from the viewpoint of the moving space platform. So, in the diagram on the right, the blue lines are the space platform's coordinate system, and the green lines are Earth's coordinate system.
It is still moving at 80% of the speed of light, even if in the opposite direction, so once again Alpha Centauri looks like it is only 2.4 light-years away due to Lorentz contraction.
This time, though, it is moving away at 80% of the speed of light. So, our FTL spaceship, moving at four times the speed of light, has to catch up with it, as if it is only moving at 3.2 times the speed of light. Therefore, it will reach Alpha Centauri, as viewed from the moving space platform, in 0.75 years, instead of in only 0.5 years, as in the first example.
And when it reaches Alpha Centauri, Alpha Centauri will be 2.4 plus 0.75 times 0.8 light-years away from the moving space platform; or 2.4 plus 0.6, or 3.
So far, so good. But what do things look like from the point of view of Earth and Alpha Centauri?
To find out, once again we need to make use of the Lorentz transformation. Since it is on Alpha Centauri that the scene of our FTL space ship's arrival lies, we are once again confident that x will work out to -4 light years.
x' equals -3, and t' equals 0.75.
The moving space platform is moving away from Alpha centauri, so v is positive 0.8c.
So x equals -3 plus 0.75 times 0.8, all divided by 0.6; this is -3 plus 0.6, all divided by 0.6, or -2.4 divided by 0.6, which is indeed -4, as expected.
Now what is t?
Well, the shock ending is clearly visible in the Minkowski diagram of how things look from the moving space platform. The purple line of the spacecraft's path lies below the x axis of Earth's reference frame.
v/c is 0.8, and x'/c is -3.
So t is equal to 0.75 plus 0.8 times -3, all divided by 0.6. That's 0.75 minus 2.4, all divided by 0.6, or -1.65 divided by 0.6, which is 2.75 years before it left Earth.
And, once again, the diagram at left which shows this uses blue lines for the coordinate system shared by the Earth and by Alpha Centauri, and green lines for the coordinate system of the space platform, since it is now showing things from the viewpoint of Earth and Alpha Centauri.
But this is just an appearance, right? Since this is happening so far away at Alpha Centauri, it doesn't involve real travel into the past of the kind that would cause a paradox, does it?
Well, that would be true, if there were no way to get anything back to Earth from Alpha Centauri at a speed faster than that of light. But because we do have the faster-than-light spaceship we used to go to Alpha Centauri, now we can use it to go back to Earth.
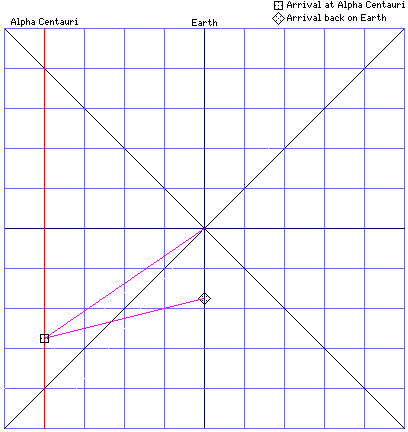
Just taking off from Alpha Centauri normally would get us back to Earth in only one year, and so that would be 1.75 years before we left, as can be seen from the diagram at right.
And nothing is stopping us from using a platform at Alpha Centauri that is moving away from the Earth at 80% of the speed of light as our jumping-off point for the return trip, which would allow us to move a further 2.75 years into the past, for a total of 5.5 years backwards in time.
As was the case for the original journey from the Earth to Alpha Centauri, Lorentz contraction means the Earth appears to be only 2.4 light-years away from the viewpoint of the space platform, but since it's going away at the rate of 0.8c, one has to divide 2.4 light-years by 3.2c rather than 4c to find that the FTL space craft will reach it in 0.75 years, at a distance of three light-years away.
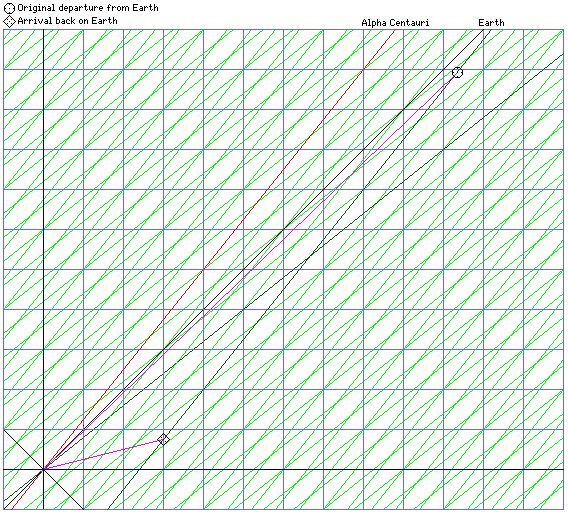
This is trivially obvious from symmetry, but just to make it more clear, I will provide Minkowski diagrams for this case as well; first, at left, from the viewpoint of the moving space platform, (and so the blue lines show the space platform's coordinate system in that diagram) now going in the opposite direction.
Note that this diagram is larger than the other Minkowski diagrams shown, in order to include the position of the space craft's original departure from Earth, as it appears in the reference frame of the moving space platform near Alpha Centauri.
Since that space platform is moving in the opposite direction as that in which the space platform near the Earth was moving, it's not surprising that the journey from the Earth to Alpha Centauri looks even more different from the way it appeared from that space platform than the way it appeared from Earth.
From the Earth's reference frame, relative to the origin of this diagram, we have:
t' = 2.75 years;
x' = 4 light years;
v = 0.8c.
So, from the Lorentz transform,
x equals 4 plus 2.2, all divided by 0.6, which is 6.2 divided by 0.6, or 10 1/3 (10.3333...) light-years in the direction of Earth from Alpha Centauri.
t equals 2.75 plus 3.2, all divided by 0.6, which is 5.95 divided by 0.6, or 9 11/12 (9.91666...) years in the future.

And then, at right, a Minkowski diagram from the viewpoint shared by the Earth and by Alpha Centauri is also presented.
Here, the blue lines are the coordinate system of that reference frame, and the green ones are the coordinate system of the space platform near Alpha Centauri from which the space craft began its return journey.