Einstein's Theory of Relativity, although it has long since ceased to be controversial within the scientific community, is still puzzling to many ordinary people who are not scientists. Sometimes, attempts to explain it to the general public even cause confusion, instead of clearing it up, because in trying to simplify the subject, they end up leaving out the most important pieces of the puzzle that explain why something so seemingly bizarre can possibly be true.
As you've no doubt heard, Einstein's theory claims that something that travels in one direction at a speed comparable to that of light will contract noticeably in the direction of motion. And, as well, time slows down for fast-moving objects.
But it isn't called the Theory of Relativity for no reason. It also claims that motion is relative, so that it isn't possible to tell which of two observers, moving relative to one another, is moving, and which one is standing still. So, from the viewpoint of a moving object, it is the object that is standing still that is getting shorter, and which is having time slow down for it.
How can this be? Wouldn't this create an obvious discrepancy, that shows this can't possibly be true?
In fact it doesn't, because of one other thing that is predicted by the Theory of Special Relativity. This prediction is called the relativity of simultaneiety.
The contraction of objects in the direction of motion, known as the Lorentz contraction, doesn't involve things getting squashed, or feeling any kind of strain or pressure. If it had, it would directly contradict the most basic principle of relativity, which led to the theory in the first place: that the laws of physics are the same in all inertial reference frames. That is, if you are in a compartment moving at a uniform rate in a constant direction, you can ignore that motion, and calculations involving the laws of physics will still work out right for things that take place within that compartment.
A kind of contraction that is relative is familiar to us from every-day observation; it is called foreshortening by artists.

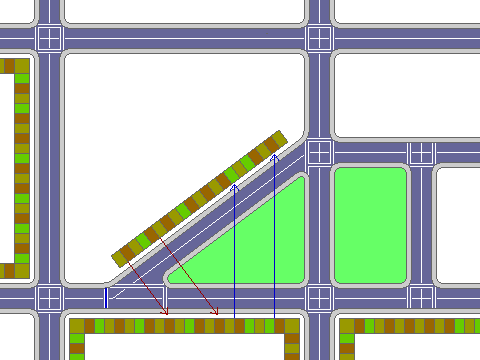
The picture above is a map of a small part of a city. On the south side of the street, there are a number of stores that are all identical small buildings - except for larger ones at the corners.
On the north side of the street, a road branches away at an angle, and on the north-west side of that road, there are also a number of stores that are identical in size. Between that angled road, and the street that it branched away from, there is a wedge-shaped block which has been made into a small park, so that people walking in front of either group of shops can see the other group of shops, although they face a different road.
As the red and blue arrows in the diagram show, if you walk past four shops in one group of shops, and then look across at the shops in the more distant group, you find that you have passed five of them. So the shops where you are walking are, in a sense, wider than the shops on the other street. But this is true whether you are on the south side of the street going east, or on the north side of the street going northeast.
Of course, there is no real contradiction; in either case, a portion of the width of the shops in the other group is along the direction you are walking, and another portion of that width is in a different direction, so the shops in both sets of shops are equally wide; they are merely oriented differently. This principle, although in a different form, is exactly what applies to time dilation and Lorentz contraction in Special Relativity as well.
A car travelling along a residential street or an alleyway that is not cleared of snow, or an ox-cart being pulled along a path on soft ground, will often find that its wheels will be moving in the tracks, or the ruts, left by the vehicles that passed that way before.
One thing that Einstein's Theory of Relativity does not predict is that a moving object will either contract or expand in a direction transverse to its motion. If a moving car contracted sideways, then if it were travelling in ruts, it would experience additional wear on the sides of its tires that faced the inside of the car. If it expanded sideways, it would experience additional wear on the sides of its tires that faced outwards.
This would be an incontrovertible fact that would have to be accepted by any observer, whether moving with the car, or standing still on the ground. Thus, for the observer on the ground to see the car becoming narrower, but for the observer in the car to see the ruts becoming narrower instead, is an impossibility.
Having this one solid fact to stand on, we can begin to derive the equations of Special Relativity.
All the strange things that Special Relativity predicts are consequences of one other thing taken as a solid fact: the premise that all light, no matter where it may have come from, when travelling in a vacuum, always appears to any observer to be moving at exactly the same speed. This premise resulted from Maxwell's equations of electrodynamics, which predicted the phenomenon of electromagnetic radiation, and gave it a speed essentially identical with what was known to be the speed of light. As this meant that the speed of light was a consequence of the laws of physics which applied to electricity and magnetism, this made that speed itself one of the basic laws of physics. Initially, it was simply assumed that this predicted speed was relative to a medium in which light travelled, called the luminiferous aether. Einstein was bold enough to consider the possibility that the speed of light could really appear exactly the same for everyone, even though this would require strange things to happen. Special Relativity looks like an elaborately contrived way of achieving a premise that doesn't seem reasonable - that the apparent speed of light does not change even though you are travelling towards or away from its source - and that's hardly surprising. That is basically what it is. It wouldn't be worth bothering with except for the fact that innumerable experiments have shown that it is exactly the way our Universe really works.
This diagram is not at all original with me, but rather similar diagrams appear in innumerable textbooks on Special Relativity.
Since, from the argument above, we've established that Relativity does not predict a contraction transverse to the direction of motion, we are able to put a number to time dilation.
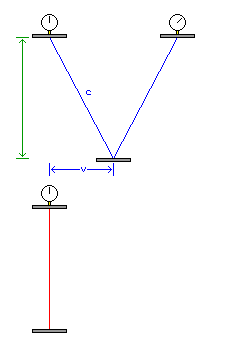
One way to make a clock would be to measure the time light takes to bounce back and forth between two mirrors separated by a known distance.
When a clock like that is carried by a moving observer, from the viewpoint of the stationary observer, the light in that clock has to travel a longer distance, because it has to cover not merely the distance between the two mirrors, but also the distance that the clock has moved. In order for the distance between the two mirrors to be known, the clock is at right angles to the direction of motion. So we have a right triangle. The hypotenuse, the side representing the distance actually travelled by light between the two mirrors, is in proportion to the speed of light, c. The base, the side along the direction of motion, is in proportion to the speed at which the clock is being moved, v.
The ratio between the hypotenuse of the triangle and the other side of the triangle, which represents the distance between the two mirrors, represents the ratio between the actual interval of time, from the viewpoint of the stationary observer, and the apparent interval of time, from the viewpoint of the moving observer, that is indicated by the moving observer's clock.
So, when one second passes for the stationary observer, from his viewpoint, only
__________
/ 2 2 _________
/ c - v / 2
\/ / v
----------------- or / 1 - ----
c / 2
\/ c
of a second passes for the moving observer.
While a clock that works by bouncing a beam of light between two mirrors is simply an imaginary device that is convenient for explaining Special Relativity, a very real piece of apparatus used in the physical sciences involves bouncing light between mirrors:
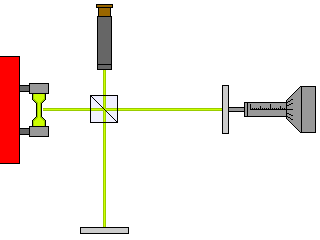
The above is a simplified diagram of an interferometer, a device used by scientists to measure the wavelength of light.
On the left of the diagram, we see a gas discharge tube which produces light composed of a number of discrete spectral lines. Optics to collimate the light from the tube, and a prism or diffraction grating to select out one spectral line of interest from that light, are left out of the diagram.
The light enters a beam splitter, the square object with a diagonal line through it in the center of the cross formed by the light beams in the four cardinal directions from it. Half the light goes downwards to the fixed mirror at the bottom of the diagram. The other half continues on leftwards, to a mirror the position of which can be shifted using the barrel of a micrometer.
When the beams of light return to the beam splitter, some of them are then reflected in the direction of a small telescope through which the experimenter can view interference between the two reflected beams of light. The distance through which the moving mirror moves between peaks and troughs of brightness in the combined beam, due to constructive and destructive interference allows the wavelength of the light under study to be determined.
The fact that the two beams of light involved are at right angles to one another is simply a convenience of how this apparatus is constructed. But it makes it simple for us to imagine an interferometer on a moving platform to provide us with further understanding of Special Relativity.
We can think of the light going downwards from the beam splitter to the mirror at the bottom as being similar to that in the clock we imagined in our previous example.
Finally, the somewhat schematic diagram below
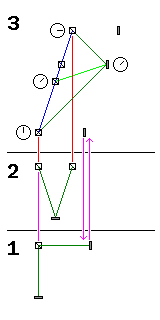
allows us to unveil the full mystery of Special Relativity.
The diagram is divided into three sections, from bottom to top.
The bottom section, marked 1, is a picture of the type of interferometer which we will be considering, when it is at rest.
The middle section, marked 2, shows how the arm of the interferometer transverse to the direction of motion behaves like the clock we met earlier when we calculated the equation for relativistic time dilation.
The top section, marked 3, is a graph of the motion of the arm of the moving interferometer that extends in the direction of its motion, from which we can derive the value of the Lorentz contraction.
On this graph, the horizontal axis represents distance along the direction of travel, as viewed by the stationary observer. The vertical axis represents time, in units such that the motion of light in the direction of motion would be shown by a diagonal line, at a precise 45 degree angle, on this diagram.
So, we see the beam splitter, with a clock next to it showing the time as perceived by the moving observer, moving at an appreciable speed, but a speed still slower than that of light, as shown by the blue line passing through four small schematic symbols for the beam splitter.
A dark green line ascends at 45 degrees from the beam splitter at an initial time, and descends at 45 degrees from the beam splitter at a final time. Since the moving observer is not to notice anything amiss because he is moving, light will leave the beam splitter, and return to it, along the arm extending in the direction of motion in the same amount of time as it does along the arm transverse to the motion, illustrated in the section of the diagram numbered 2. This reminds us that we will have to make use of what we have worked out before for time dilation when locating the items in this section of the diagram from the stationary observer's point of view.
The point at which those two lines meet is where the light has hit the mirror to be reflected back to the beam splitter. From the moving observer's point of view, of course, the light in both arms of the interferometer moves an equal distance in both directions, and so this represents the halfway point in the time involved. A small clock face is illustrated next to the mirror at this point to show this.
The horizontal distance between the mirror at this point, and the blue line representing the path of the beam splitter, shows the distance between the beam splitter and the mirror as viewed by the stationary observer. Thus, the mirror is drawn again, at that same distance from the beam splitter, at the beginning and end of the beam splitter's journey as shown.
Purple vertical lines connecting the section of the diagram marked 1 and the mirror and beam splitter at the bottom of part 3 of the diagram show that the moving mirror and beam splitter appear to be closer together, from the viewpoint of the stationary observer; this is the Lorentz contraction.
In the diagram at the top, there is also a light green line. It connects the beam splitter, at the halfway point in its journey, to the mirror at the point where, and the time when, it reflects the light back to the beam splitter.
From the point of view of the moving observer, as indicated by the clock faces, both events - the halfway point in the beam splitter's journey, and the reflection of the light that came from the beam splitter at the beginning of its journey and returned to it at the end of its journey, took place at the same time. But from the point of view of the stationary observer, as can be seen by the fact that the light green line slopes upward, the reflection at the mirror took place later.
Because, from the moving observer's point of view, it is the same time at the beam splitter as it is at the mirror after it has had some additional time to move forward from the stationary observer's point of view, it becomes possible for the moving observer to see the distance between his moving beam splitter and mirror as being greater than that between the stationary beam splitter and mirror, even though the stationary observer sees exactly the reverse.
This is why I drew the analogy at the beginning between the Lorentz contraction and foreshortening. It is relative between the two observers, because the two observers are merely rotated relative to each other - but this rotation involves time as well as space.
In addition to illustrating the phenomena of Special Relativity qualitatively, because we have the formula for time dilation in hand, we can also use it to derive the formula for the Lorentz contraction.
Given an interferometer, the arms of which are both of length d, and which is moving along the direction indicated by one of those arms (the other being at right angles to that direction) with a velocity v,
we know from the previous calculation of time dilation that, while it will seem to an observer moving with this interferometer that it will take light a time 2d/c to travel from the central point of the beam splitter to the two mirrors at the ends of the arms of the interferometer and then back again, from the viewpoint of a stationary observer, the elapsed time will instead be:
2d
--------------------
__________
/ 2
/ v
c / 1 - ----
/ 2
\/ c
and the distance travelled by the interferometer, again from the viewpoint of the stationary observer, will be v times that.
If we take the initial position of the center of the beam splitter in the moving interferometer, when the light leaves it to go out into the two arms, to be x0=0, at t0=0, then its final position, when the light returns to it from the two arms, will therefore be:
2dv
x = --------------------
f __________
/ 2
/ v
c / 1 - ----
/ 2
\/ c
at
2d
t = --------------------
f __________
/ 2
/ v
c / 1 - ----
/ 2
\/ c
The first item we must solve for is the time and position, from the viewpoint of the stationary observer, when the light strikes the mirror in the arm in the direction of motion to be reflected back. This time and position will satisfy the following two equations:
1) x = c t
r r
2) x - x = c ( t - t )
r f f r
with xf and tf as defined above.
Applying those definitions to (2), we get:
3) x - vt = c ( t - t )
r f f r
and substituting from (1), we obtain:
4) x - vt = ct - x
r f f r
Collecting terms, this becomes:
5) 2x = (v+c)t
r f
which, from the definition of tf above, yields:
2d(v+c)
6) x = --------------------
r __________
/ 2
/ v
2c / 1 - ----
/ 2
\/ c
What we want, however, is the apparent length of the longitudinal arm of the interferometer, to compare it with d, so as to obtain the extent of the Lorentz contraction. This apparent length is:
7) L = x - vt
r r
note that it is vtr and not vtf which is subtracted, and from (1), that is a simple multiple of xr, as follows:
v v 2d(v+c)
8) L = x - --- x = ( 1 - --- ) --------------------
r c r c __________
/ 2
/ v
2c / 1 - ----
/ 2
\/ c
thus, the factor by which the length of something subject to the Lorentz contraction is to be multiplied, L/d, is:
_________
/ 2 2 __________
2 2 / c - v / 2
L (c-v)(c+v) c - v \/ / v
9) --- = -------------------- = ----------------- = --------------- = / 1 - ----
d __________ _________ c / 2
/ 2 / 2 2 \/ c
2 / v c / c - v
c / 1 - ---- \/
/ 2
\/ c
which is the same factor as we derived above for time dilation.
But we are not content to stop here. As we saw from our qualitative discussion of the third and topmost part of the diagram above, from the point of the moving observer, the time marking the halfway point in the moving interferometer's journey is not reached at the same time (from the stationary observer's point of view) at the beam splitter and at the mirror at the far leading end of the longitudinal arm of the interferometer.
Thus, we are filled with curiosity (well, those of us who haven't been long since frightened away by the quantity of algebra above, at least) as to the coordinate transform between the coordinate system of a stationary observer and that of a moving observer in Special Relativity.
It should not, at this point, spoil any surprise to say that the following diagram

sums up the basic qualitative features of the relativistic co-ordinate transform. The coordinates shown in blue are those of the stationary observer, those shown in red are those of the moving observer. The x coordinate of the graph is space along the direction of motion (as we noted earlier in our discussion of wheels in ruts, the space coordinates perpendicular to the direction of motion do not change in Special Relativity), and the y coordinate of the graph is time, in units such that the speed of light, although very fast by our standards, is taken to be unity. Thus, the diagonal lines in black represent light going through the origin in two opposite directions.
The fact that the speed of light is constant for all observers is shown by the fact that these two lines, whose equations are y=x and y=-x, have these same equations in the coordinate system shown in red, because of the way in which the rhombi of which it is composed are symmetrical about the diagonal axes of the diagram.
The fact that each observer perceives the other observer's coordinate system to be the one affected by the Lorentz contraction and by time dilation is shown by how the coordinate lines cross about midway between the axes of the stationary and moving coordinate systems, thus giving an equal but inverse ratio between the two systems in each other's terms.
This kind of diagram, of course, is the one known as a Minkowski diagram.
And, the coordinate transform is, where v is the velocity in the positive x direction of the moving observer, and where x', y', z' and t' are the coordinates of events in the frame of the moving observer, while x, y, z, and t are those in the frame of the stationary observer, as the diagram strongly suggests, and as can be seen from the interferometer example above,
x' + vt'
x = ------------------
__________
/ 2
/ v
/ 1 - ----
/ 2
\/ c
y = y'
z = z'
vx'
t' + ----
2
c
t = ------------------
__________
/ 2
/ v
/ 1 - ----
/ 2
\/ c
The first equation simply takes the Lorentz contraction and time dilation into account in a straightforward manner, and acknowledges the relative velocity of the moving frame. The second and third equations simply show the initial assumption we made to obtain the value of time dilation.
Only the fourth equation is really new, and it is simply a version of the first equation, appropriately scaled, to represent the fact that time and space move together in an equal amount when an object is, through its motion, rotated in spacetime.