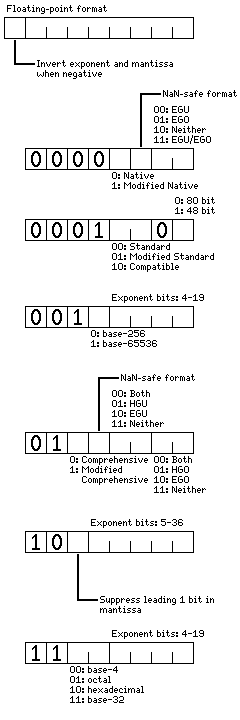
The field in the program status block which indicates the floating-point format in current use by the computer has the form shown below:

These formats are divided in two basic groups: simple formats, in which the form of the exponent is uniform from one precision to another, and which are described by the individual bits in the field, and complex formats, which correspond to a particular format of importance. The Native, Standard, Compatible, and Comprehensive formats are the complex formats, and the Native format is the default floating-point format.
Note that although it is possible to specify floating-point formats where the exponent indicates a power of 8, such formats are only available when an alternate memory width is in use.
The illustration below

shows what the complex formats are like, and include a simple format closely related to the compatible format, which is termed the modified compatible format. This format is the simple format represented by the value 000111010 in the field.
The other formats are described fully above; where the exponent is binary, leading one suppression means that the binary point precedes a one bit appended to the mantissa in the format except for the zero exponent value; the zero exponent value can be associated with an unnormalized value or a zero mantissa.
When leading one suppression is selected for any of the simple formats, in order to avoid having to use more than 128 bits for the floating-point arithmetic unit, the format does become complex in a standardized way: the exponent field is increased in size by four bits, and leading one suppression is not used, for 128-bit precision.
For the simple formats, except when a nonzero value appears in the exponent offset field of the Program Status Block, the exponent of a floating-point number is in excess-n notation, where n is that power of two which most nearly divides the exponent range in half, and where the binary point of the mantissa is considered to immediately precede the most significant bit of the mantissa, except where there is a hidden first bit specified for an exponent which is a power of two, in which case the binary point immediately precedes the hidden first bit.
The available simple formats allow formats to be chosen which correspond to a wide range of computers that have been available, but they do not cover all the possibilities that have been used historically. Except for the RECOMP II computer, whose floating-point format must find its equivalent among the possibilities for the Simple Floating format, a form of floating-point number processed by this computer's fixed-point arithmetic units, however, and for computers which provided NaN handling prior to the advent of the IEEE-754 floating-point format, the attempt has been made to provide sufficient flexibility as to provide the means of specifying a floating-point format which is equivalent, in terms of precision and numeric range, to that of almost all computers that have been used in practice, thus providing equivalency from the viewpoint of the higher level language programmer whose programs include no dependencies on the precise details of the format used. One other exception is that there is no provision for unused bits in a floating-point format, and so the nearest match to the floating-point formats of some machines will be one with additional precision.
The bit which indicates that the exponent and mantissa fields are to be complemented when the number is negative calls for bit inversion, or the one's complement, in that case; not the two's complement, which could cause effects that cross field boundaries, as used in the Sigma series computers from Scientific Data Systems and in the Digital Equipment Corporation PDP-10.
This bit governs transfers in and out of the floating-point registers, and can be altered without invalidating their contents; changing any other part of the floating-point format, as a general rule, does invalidate all the contents of the floating-point registers to which the floating-point format applies: the floating-point registers, the supplementary floating-point registers, the long vector registers, the long vector scratchpad, the short vector registers, and the three floating-point accumulators used by code 0 microprograms.
Note that while the intent of this bit is to allow floating-point numbers to be compared as if they were two's complement integers, setting this bit will not achieve this result for all floating-point formats. In particular, unnormalized values will not collate correctly, coded symbols which represent NaNs will not collate correctly, and numbers involving the use of the Extremely Gradual Underflow/Overflow feature will not collate correctly.
The complex formats involve such things as:
and they are described below.
In native mode, the exponent field is 11 bits in width for all precisions except the 128-bit quad precision. It is considered to be an integer represented in excess-1024 notation, by two to the power of which the mantissa, with an implied binary point in front of its first bit, is multiplied.
This is true when the mantissa is normalized. If there is a leading zero bit in the mantissa, and Extremely Gradual Underflow is specified, but Extremely Gradual Overflow is not specified, then the exponent value is adjusted downwards by 2047, so that the range of floating-point values expressed by values with one leading zero continues on downwards from those expressed without a leading zero bit:
0 00000000001 1000... 2^(-1024) (2^(1-1024) * 0.5) 0 00000000000 1000... 2^(-1025) (2^(0-1024) * 0.5) 0 11111111111 0100... 2^(-1026) (2^(2047-3071) * 0.25) 0 11111111110 0100... 2^(-1027) (2^(2046-3071) * 0.25) ... 0 00000000000 0100... 2^(-3073) (2^(0-3071) * 0.25) 0 11111111111 0010... 2^(-3074) (2^(2047-5118) * 0.125)
and an additional downwards adjustment of 2047 is made for each additional leading zero bit. This avoids the complications of having a hidden zero bit, and avoids the waste of information involved in having a bit in the representation of a floating-point number that is always equal to one.
Since shifting something one place left is equivalent to multiplying it by two, decoding these numbers is very simply implemented by just changing the part of the exponent incremented as one normalizes the mantissa; shifting the mantissa one place left decrements the exponent by 2048 instead of one. Using a shift network instead of serial shifting for normalization is also not in any way precluded.
The Quad Precision mode provides a 23-bit exponent, so as to accomodate the extended numeric ranges provided by means of extremely gradual underflow and overflow, if used.
It may be noted that I originally thought of Extremely Gradual Underflow because I found the fact that the two smallest values of the exponent in the IEEE 754 standard multiplied the mantissa (or significand) bits by the same value to be inaesthetic; this is avoided if the leading 1 bit is not hidden, but then there is the inefficiency of that bit being wasted. So I devised the format to show that one could have a bit-efficient format that did not hide the leading 1 bit.
Compared to the IEEE 754 format, however, it is much less practical; at the bottom of the exponent range, the "hole around zero" still exists, but at a far smaller scale than would be the case with a conventional floating-point notation. The extra very small numbers that can be coded in this fashion are little used, so storage is not really saved to the same extent as would be the case from suppressing the leading 1 bit.
Thus, from a practical point of view, this form of floating-point is inferior to IEEE 754. In low-precision versions, however, it may be useful for audio encoding, and, in fact, A-law encoding resembles a modification of this format.
In standard mode, the computer attempts to operate in a fashion which offers compatibility with implementations of the IEEE 754 floating-point standard. This standard involves different sizes of exponent fields for different floating-point precisions. In this mode, the 80-bit temporary real format is the data type used with the floating-point instructions that normally work with 48-bit floating-point numbers in other modes; both lengths allow for alignment to 16-bit boundaries only. As well, in addition to the types included in the standard, a 128-bit quad precision format is provided, which is essentially the same as the 80-bit temporary real format, but with additional bits of precision appended.
An option is provided to replace the 80-bit temporary real format with a 48-bit format. This format does hide the first bit of the mantissa, like the 32-bit and 64-bit formats, and is generally treated as a conventional real format rather than one for temporary storage of intermediate results; as well, it has one fewer bit provided for the exponent than the 64-bit format, to provide the maximum possible precision while providing an exponent range sufficient to meet typical expectations.
Compliance with the IEEE 754 floating-point standard will be included in the area of rounding; the technique of using a sticky bit as well as a guard bit, so as to distinguish between 0.5000...001 and 0.49999..., or an equivalent technique, will be used. However, the square root function, which, unlike functions such as the trigonometric and logarithmic functions, is also required to produce the most accurate results possible by this standard, may be non-compliant in some implementations. Also, it is possible to turn off guaranteed rounding to the closest possible result for division in order to increase the speed of that operation.
The implied decimal point is always before the first digit of the mantissa, and where there is a hidden 1 bit, it is immediately before the hidden one bit.
The IEEE 754 floating-point standard also provides for some combinations of bits to represent special values; such a special value is called a NaN, for "Not a Number". This type of facility also appeared in the IBM 7030 or STRETCH computer, where floating-point numbers could be in the XFP or XFN exponent ranges, indicating infinities or infinitesimals.
Specifically, in the 32-bit and 64-bit formats, only the exponents from 000...01 to 111...10 are processed normally. When the exponent is all zeroes, it is treated as if it is 000...01 for purposes of determining what is to be multiplied with the mantissa, but the hidden first bit is now a zero instead of a one. When the exponent is all ones, the mantissa portion of the number contains a code representing a special value, such as infinity.
In the 80-bit and 128-bit formats, the all-zeroes exponent is processed normally, but the all-ones exponent is still used to indicate special values.
With the all-ones exponent, an all zero mantissa indicates infinity. The sign bit indicates if the infinity is positive or negative, and it is possible for zero to be signed as well. Any other value with 0 as the first bit of the mantissa is a "Signalling NaN", which leads to an error condition; a value with 1 as the first bit is a "Quiet NaN", which does not.
The standard does not appear to define any NaN values; the Intel 8087 chip used one Quiet NaN value, one with a mantissa of 110...00 and a negative sign, to indicate an indeterminate real quantity.
Note also that some documentation of implementations of the IEEE-754 standard give a different value for the exponent bias than shown here. This is because these accounts also give a different position for the implied binary point; for consistency with other formats, the magnitudes of mantissas are held here to be less than one rather than less than two; as previously noted, the implied decimal point is always before the first digit of the mantissa, and where there is a hidden 1 bit, it is immediately before the hidden 1 bit.
The Comprehensive format introduces an additional way of extending the exponent range of numbers, Hyper-Gradual Overflow, and its counterpart, Hyper-Gradual Underflow.
When Hyper-Gradual Overflow is in effect, exponents, normally in excess-n notation, are treated normally unless they begin with 11.
If an exponent begins with 110, the exponent field is lengthened by two bits; if an exponent begins with 1110, the exponent field is lengthened by four bits, and so on.
This process ceases when the width of the mantissa field decreases to 16 bits; once this happens, the exponent can continue to increase to its all-ones value without widening further.
This format provides a significantly greater extension of exponent range than extremely gradual underflow.
Its counterpart, Hyper-Gradual Underflow, treats exponents that begin with 00 in an analogous special manner. An exponent that begins with 001 causes the exponent field to lengthen by two bits, an exponent field that begins with 0001 causes the exponent field to lengthen by four bits, and so on.
In both cases, the successively extended exponent fields are used to represent successively more extreme portions of the exponent range.
For the single-precision format, the rule is changed somewhat, since the available precision and exponent range are both very limited. Here, exponents must begin with at least 0000 or 1111 before they are treated in a special manner. In addition, for each additional consecutive 0 or 1, the exponent is lengthened by four bits, so that a wide range of exponents can be provided despite the limited width of these numbers. However, to prevent sudden jumps in the length of the exponent, which would mean that the last three bits of precision for the preceding exponent are, in effect, wasted, because immediately adjacent quantities are less precise, the two bits following the stretch of consecutive zeroes or ones at the beginning and the opposite bit that terminates that stretch are also taken into consideration. This is referred to as modified hyper-gradual underflow.
Thus, for the single-precision floating-point format, in which the exponent begins as a seven-bit value in excess-64 notation, and widens to a maximum size of 15 bits, exponent values are interpreted in this fashion when both hyper-gradual overflow and hyper-gradual underflow are used:
111111111111111 725 111111000111111 277 111111000000000 214 11111011111111 213 11111011000000 150 1111101011111 149 1111101000000 118 111110011111 117 111110000000 86 11110111111 85 11110110000 70 1111010111 69 1111010000 62 111100111 61 111100100 58 11110001 57 11110000 56 1110111 55 1110000 48 1101111 47 1100000 32 1011111 31 1000000 0 0111111 -1 0100000 -32 0010000 -33 0010111 -48 0001111 -49 0001000 -56 00001111 -57 00001110 -58 000011011 -59 000011000 -62 0000101111 -63 0000101000 -70 00001001111 -71 00001000000 -86 000001111111 -87 0000011100000 -118 0000011011111 -119 0000011000000 -150 00000101111111 -151 00000100000000 -214 000000111111111 -215 000000111000000 -278 000000000000000 -726
Hyper-gradual underflow, particularly when a minimum allowed precision of 16 bits is specified, clearly does not fill in the "gap" around zero that is filled in by plain gradual underflow as used in the Standard format: if the extremely low exponents this format can represent are thought of as an important part of the numeric range, the gap is still there. This is also a characteristic of extremely gradual underflow; only simple gradual underflow actually avoids a gap around zero, the others simply shrink it to what may be an absurdly small size. Thus, if extremely gradual underflow is not specified with this format, whether or not hyper-gradual underflow is specified, the practice in the Standard format is followed, and the leading one bit of the mantissa is not suppressed for the minimum possible exponent value to allow gradual underflow to be used.
When extremely gradual underflow or extremely gradual overflow are specified in the absence of hyper-gradual underflow or overflow, the leading 1 bit of the mantissa is no longer suppressed.
When extremely gradual overflow and extremely gradual underflow are specified to be used in conjunction with hyper-gradual overflow and hyper-gradual underflow respectively, a more complicated modification to the format is made.
Hyper-gradual overflow and underflow work normally as the mantissa shrinks in size down to 18 bits in length.
An additional leading 0 or 1 in the exponent will then expand the exponent field by one bit instead of two, and the leading 1 bit of the mantissa will not be suppressed for the case where the exponent field has its maximum length, and the mantissa field is 17 bits long, only.
Thus, for each additional leading zero in the mantissa field, the exponent field will only run over all possible values that it takes when it has maximum length, because for all other lengths of the exponent field, the leading one bit of the mantissa field is suppressed, and extremely gradual underflow and overflow are not possible.
Note that this means, since the exponent field runs to the end of its range without further lengthening when it is at its maximum length, that the final lengthening only doubles the range of the exponent field, as all previous lengthenings did, and thus lengthening it by one bit at the end is a reasonable compromise so that the lengthening, plus the reappearance of the leading 1 bit of the mantissa, causes, as with all previous exponent lengthenings, a loss of two bits of precision in the number rather than a loss of three bits of precision.
If NaN-safe mode is selected, each bit of additional unnormalization for extremely gradual overflow will have one less exponent value to run over in this circumstance; this is, of course, true in general for extremely gradual overflow.
With all those features selected, the range of exponents then looks like this:
11111111111111 NaN codes 11111111111110 [1] 532 [01] 851 [001] 1170 ... [00000000000000001] 5636 11111011111111 [1] 277 [01] 596 [001] 915 ... [00000000000000001] 5381 11111011000000 [1] 214 [01] 533 [001] 852 ... [00000000000000001] 5318 11111010111111 213 11111010000000 150 1111100111111 149 1111100100000 118 111110001111 117 111110000000 86 11110111111 85 11110110000 70 1111010111 69 1111010000 62 111100111 61 111100100 58 11110001 57 11110000 56 1110111 55 1110000 48 1101111 47 1100000 32 1011111 31 1000000 0 0111111 -1 0100000 -32 0010000 -33 0010111 -48 0001111 -49 0001000 -56 00001111 -57 00001110 -58 000011011 -59 000011000 -62 0000101111 -63 0000101000 -70 00001001111 -71 00001000000 -86 000001111111 -87 0000011100000 -118 0000011011111 -119 0000011000000 -150 00000101111111 -151 00000101000000 -214 00000100111111 [1] -215 [01] -535 [001] -855 ... [00000000000000001] -5335 00000011111111 [1] -278 [01] -598 [001] -918 ... [00000000000000001] -5398 00000000000000 [1] -534 [01] -854 [001] -1174 ... [00000000000000001] -5654
The square brackets show the leading bits of the mantissa up to the first 1 bit in the mantissa. Thus, it can be seen that although extremely gradual overflow and underflow do not increase the range of possible exponents for each level of reduced precision in the same way as hyper-gradual underflow and overflow do, they still do provide a considerable extension of the exponent range.
Note that for the exponent ranges from -151 to -214, and from 150 to 213, the leading 1 bit of the mantissa remains suppressed, for an additional bit of precision, and so these maximum length exponents are not included in the range covered by extremely gradual underflow and overflow.
In compatible mode, the computer provides compatibility with the floating-point format of the IBM System/360. This includes the format of 128-bit quad precision numbers, as introduced with the IBM System/360 Model 85, which have a second part that looks like an unnormalized floating-point number having the correct value for the second half of the number (unless, of course, the exponent of the number is less than 14 minus 64, in which case the exponent will have experienced an integer underflow). A 48-bit floating-point type in the same general format is provided, in addition to the types supported by that machine.
In modified compatibility mode, the 128-bit floating point format is changed to just offer a continuous mantissa, and thus 8 additional bits of precision, but otherwise the computer uses the System/360 floating point format in this mode as well.
In the short vector registers, floating-point numbers have the same precision and format inside the registers as they do in memory.
In all the other floating-point registers (the floating-point registers, the supplementary floating-point registers, the floating-point long vector registers, and the floating-point long vector scratchpad), because an entire 128-bit wide register is used for a single floating-point number, floating-point numbers have a different format when within a register than in memory, for two reasons: to speed and simplify computations, by eliminating complicated aspects of the floating-point format, and to preserve precision by including guard bits.
This practise is well known from the IEEE-754 floating-point format, in which the temporary real format had been explicitly specified. Since older architectures did not retain guard bits between operations, and since the presence of guard bits can lead to the results of a calculation being affected by whether or not intermediate results are kept in registers, the option of disabling these guard bits is provided.
Also, just as the load instructions for the integer registers perform sign extension, when a floating-point register is loaded with a value, normally the less significant portion of the register not used with the type of the instruction is filled with zeroes. When the value in the register is saved, then the rounding mode specified in the program status doubleword is applied.
However, if round on load, truncate on store, is specified, then when a floating point register is loaded with a value, the less significant portion of the register which is not filled by the input value is only loaded with zeroes when the input value is zero; otherwise, it is filled with 1000...0000. In the round on load, truncate on store mode, nonzero floating-point values in precisions less than the maximum are considered to be implicitly truncated instead of implicitly rounded.
Note that in addition to these additional guard bits, retained in registers between operations, one guard bit is associated with an illustrative implementation of floating-point arithmetic that accompanied the IEEE-754 standard to show how it was possible to consistently achieve the best possible result for the four basic arithmetic operations and square root, as that standard also required. This is the guard bit belonging to the set of guard, round, and sticky bits. As there are two kinds of guard bits, and several basic types of floating-point register in this architecture, some potential for confusion exists about which features are provided with which format. The following table, therefore, summarizes the association of the different kinds of guard bits with the different kinds of floating-point number and the different floating-point operation units.
| Floating-point Type | Guard, Round, and Sticky Bits | Additional Guard Bits |
| Floating-Point Shorter than 128 bits in Regular Floating-Point Registers | Yes | Yes |
| 128-bit Floating-Point | Yes | No |
| Floating-Point in Short Vector Registers | Yes | No |
| Simple Floating Type | No | No |
On this computer, the associated temporary formats for each floating point precision within Standard format are as follows:
For 32-bit floating-point numbers, the temporary format corresponds to the temporary real format in terms of its layout and the size of its exponent field, but is only 48 bits in length.
For 64-bit floating-point numbers, the temporary format is the 80-bit temporary real format.
For 80-bit floating-point numbers, the temporary format is 88 bits long, corresponding to temporary real format with eight additional guard bits.
For 128-bit floating-point numbers, the temporary format and the external format are identical.
Again to avoid complexity, hyper-gradual overflow and underflow, in addition to extremely gradual overflow and underflow, which are also available in the comprehensive format, are omitted in the format of 128-bit floating-point numbers, and the exponent field is increased significantly in size, so that this format can subsume internal real number formats which can be used with the other precisions.
The exponent is made twenty bits longer, and so the 128-bit format can handle numbers both larger and smaller than those allowed by the use of extremely gradual overflow or underflow, and hyper-gradual overflow or underflow.
For 32-bit floating-point numbers, the temporary format corresponds to the 128-bit format in arrangement, and is 64 bits in size.
For 48-bit floating-point numbers, the temporary format corresponds to the 128-bit format in arrangement, and is 76 bits in size.
For 64-bit floating-point numbers, the temporary format corresponds to the 128-bit format in arrangement, and is 92 bits in size.
For 128-bit floating-point numbers, the temporary format and the external format are identical.
Note that in the case of 32-bit floating point numbers, a temporary format of 64 bits in size is not inherently necessary; 19 bits of the exponent will not be used, but are present in the temporary format because most of them are required to represent the numeric range available in the 64-bit format.
Because the size of the exponent field does not need to be expanded with the formats based on those of the IBM System/360, temporary formats are only made longer in order to add guard bits. Thus, they are only 8 bits, rather than 16 bits, longer than their corresponding external formats.
In the case of 128-bit numbers, the internal format of a 128-bit floating point number in Compatible mode is its format in Modified mode, so, uniquely in Compatible mode, even the 128-bit floating-point numbers receive guard bits for register operations.
Since during an interrupt, the entire 128 bits of a floating point register are saved and restored, normally returning from an interrupt is not complicated by using guard bits with shorter formats. This unique feature of Compatible mode might seem to potentially complicate this; however, since an interrupt service routine is not necessarily running in the same mode, including the same floating point format, as was selected by the process that was running during the interrupt, it is expected that the 128-bit entries in a context block for loading into the floating-point will be so loaded, upon return from an interrupt, in a direct binary fashion.
It is thus envisaged that the floating-point arithmetic unit would be implemented such that the internal formats referred to here are the actual internal formats; loads and stores to memory would vary depending on operand type and format type, but as all the internal formats for a given floating-point format for the different operand lengths have the same length of exponent, the format-dependent transformation between the registers and the floating-point ALU is relatively simple, almost the only difference between the three different internal formats being the location of the boundary between exponent and mantissa. Of course, some additional circuitry is needed to cope with the fact that the exponent for the Compatible and Modified floating-point formats is a power of sixteen instead of two.
The floating point formats available in this architecture have the following approximate ranges:
Native (any options)
Quad
-78914 78912
3.1030 * 10 to 8.0566 * 10
-262144 262143
( 0.5 * 2 to 0.9999... * 2 )
Native (with extremely gradual underflow)
Floating, Medium, and Double
with full precision
-309 307
2.7813 * 10 to 8.9884 * 10
-1,024 1,023
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to
Floating
-10,217
8.8112 * 10
-33,936
( 0.5 * 2 )
Medium
-21,887
4.1131 * 10
-72,704
( 0.5 * 2 )
Double
-31,751
2.9058 * 10
-105,472
( 0.5 * 2 )
Standard
Floating (Short Real)
with full precision
-38 38
1.1750 * 10 to 3.4028 * 10
-125 128
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to
-45
1.4005 * 10
-148
( 0.5 * 2 )
Double (Long Real)
with full precision
-308 308
2.2164 * 10 to 1.7977 * 10
-1,021 1,024
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to
-324
4.9204 * 10
-1,073
( 0.5 * 2 )
Temporary Real and Quad
with full precision
-4,933 4,931
8.4053 * 10 to 5.9487 * 10
-16,383 16,383
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to
Temporary Real
-4,952
9.1130 * 10
-16,446
( 0.5 * 2 )
Quad
-5,000
6.2354 * 10
-16,606
( 0.5 * 2 )
48-bit
with full precision
-157 154
2.9134 * 10 to 1.3408 * 10
-519 512
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to
-168
2.1198 * 10
-556
( 0.5 * 2 )
Compatible (and Modified Compatible)
All sizes
-79 75
5.3976 * 10 to 7.2370 * 10
-64 63
( 0.0625 * 16 to 0.9999... * 16 )
Comprehensive (with any options)
Quad
-323,228,497 323,228,496
1.19128 * 10 to 2.0986 * 10
-1,073,741,824 1,073,741,823
( 0.5 * 2 to 0.9999... * 2 )
Comprehensive (with hyper-gradual underflow and hyper-gradual overflow)
Floating
with full precision
-18 16
6.9389 * 10 to 3.6029 * 10
-56 55
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to and up to
-219 218
1.4164 * 10 to 1.7650 * 10
-726 725
( 0.5 * 2 to 0.9999... * 2 )
Medium, and Double
with full precision
-155 153
3.7292 * 10 to 6.7039 * 10
-512 511
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to and up to
Medium
-473,326 473,324
3.8303 * 10 to 6.5270 * 10
-1,572,352 1,572,351
( 0.5 * 2 to 0.9999... * 2 )
Double
-121,210,533 121,210,531
3.9149 * 10 to 6.3859 * 10
-402,652,672 402,652,671
( 0.5 * 2 to 0.9999... * 2 )
In each case, the numbers indicated in the range, zero, and negative numbers having the same range of magnitudes can be represented in the format.
Note that the numbers in the IEEE 754 format which have an exponent field of zero, and which have an explicit first one bit in the first position of the mantissa, have a precision which is reduced by one bit compared to that of numbers with a nonzero exponent field, and therefore they do not have maximum precision, but these numbers are still classed as normalized numbers rather than denormalized ones; thus, the lower end of the range of numbers with maximum precision will be twice as large as the lower end of the range of normalized numbers as you may have seen in other references.
(Incidentally, if you were wondering, I either calculated these numbers by first taking 1.024 or 0.9765625 to suitable powers, in order to remain within a more restricted range of numbers, or, in more extreme cases, I simply worked directly with an accurate value of the common logarithm of 2.)
For the native floating-point format, the ranges quoted above apply only to the default mode of operation, with extremely gradual underflow only.
For that mode, the last two bits of the field indicating the floating-point format are used to select whether the degree of unnormalization of a number is used to extend the exponent range downwards, upwards, or both.
Their values are:
00: Neither Extremely Gradual Underflow nor Extremely Gradual Overflow 01: Extremely Gradual Underflow and Extremely Gradual Overflow 10: Extremely Gradual Underflow only 11: Extremely Gradual Overflow only
With extremely gradual overflow, instead of decreasing the exponent by a full range less one for each leading zero bit found in the mantissa, the exponent is increased by a full range less one.
With both extremely gradual overflow and extremely gradual underflow in effect, when there is at least one leading zero bit in the mantissa, the exponent field is split into two ranges, one with a first bit of 0, for which extremely gradual underflow takes place, and one with a first bit of 1, for which extremely gradual overflow takes place. Thus, the change in the exponent for each leading zero bit is halved, and so precision is lost twice as quickly in exchange for extending the numeric range in both directions.
It is possible to specify the Native format without either gradual underflow or overflow because this format offers other special features as well, and thus no standard format would be fully compatible with that format except for these features.
As it was necessary to provide the machine with circuitry to handle infinities as marked numbers for the Standard floating-point format, an option is provided to use them with the Native floating-point format as well, although their handling with that format is considerably different.
If the NaN-safe mode bit is set, then handling of floating-point numbers in native format is modified as follows:
The maximum possible exponent value, instead of indicating a large number, indicates a NaN. For the standard NaN values defined here, the entire mantissa field is zero except for the last fifteen bits. (Note that, thanks to the minimum precision condition, this is compatible with the use of hyper-gradual overflow in the Comprehensive floating-point format.)
An alternative option, of using the exponent field for numbers with a zero mantissa, would more efficiently utilize available bit combinations, but would preclude using unnormalized arithmetic; since unnormalized arithmetic, by preserving significance, is useful for purposes of numeric analysis, it should be possible to combine it with the use of NaN codes.
To achieve compatibility with extremely gradual overflow, in the case where extremely gradual overflow is present, whether alone or in combination with extremely gradual underflow, and NaN-safe operation is indicated, the maximum possible exponent value for which there are fifteen bits remaining in the mantissa field after its most significant one bit is the one which indicates a not-a-number value, and higher, less normalized positive exponents are not available.
To achieve compatibility with extremely gradual underflow used alone, the maximum possible exponent value indicates a NaN when the number is fully normalized.
Note that in both these cases, the mantissa does contain the 1 bit that indicates degree of unnormalization, and is not entirely zero except for the fifteen bits indicating the type of not-a-number value.
In addition to these possibilities, which can be automatically generated when an arithmetic operation is unable to produce a valid numeric result, when the bit preceding the last fifteen bits is a one, then manually introduced NaN codes, which are simply propagated using the rule that the larger one takes precedence, are handled; the possible codes represent 16,384 possible quiet NaNs, followed by 16,384 possible signalling NaNs.
The NaN field indicates the possible values that an invalid number might have; its fifteen bits stand for the following possibilities in order:
Thus, the result of dividing zero by zero will have an NaN field of 111111111111111, and the result of dividing any other valid floating-point quantity by zero will have an NaN field of 100000000000001.
Infinitesimals that cannot be zero can be formed by dividing by infinity, and underflows that cannot be zero can be formed by dividing a sufficiently small number by a sufficiently small number, and they are useful since dividing by them yields less ambiguous results than dividing by zero.
When the NaN-safe bit in the floating-point format field of the Program Status Block is not set, NaN quantities are not used with the Native floating-point format.
Not all possible values of the NaN field are used. 1, 0, and -1 all are numbers that can be represented as normal floating-point numbers, and will preferably be so represented. As well, any combination including zero as a possibility, and only additionally including one or both infinitesimals, will be converted to a normal zero.
In general, an operation between two NaNs of this type will produce a result that is the OR of the results of that operation between each individual bit that is set in the two operands.
In the Standard format, following IEEE 754, and unlike the case in other floating-point formats, -0 and +0 are treated as distinct numbers. Note that this can sometimes lead to incorrect results, where a division by an actual zero which is not an infinitesimal produces a NaN which is definitely either positive or negative infinity, instead of one which may be either. Forcing all infinite values to be projective, which was an option offered with the 8087 chip dropped from the actual IEEE 754 standard, does not solve this problem. However, it is said that -0 and +0 as they appear in the current IEEE 754 standard can be useful to deal with situations such as distinguishing between 180 degrees west longitude and 180 degrees east longitude when drawing a map, and analogous situations involving cuts and boundaries in complex arithmetic.
It is possible to select a Modified Native format, and a Modified Standard format, for floating-point numbers.
Both the Native and Standard formats offer features useful in performing accurate floating-point calculations. However, neither the Standard format, nor the Native format if extremely gradual underflow or extremely gradual overflow is in use, is compatible with unnormalized floating-point operation, which is also useful when the accuracy of calculations is a concern, as it allows keeping track of significance.
Thus, modified forms of each of these formats are provided which sacrifice one bit of precision in order to allow unnormalized operation.
In the Modified Standard format, the Modified Native format and the Modified Comprehensive format, in addition to the sign bit and the exponent field at the beginning of the number, and the mantissa field following, a padding field is added to the end of the number. This padding field may consist of a single 0 bit, or it may consist of a 0 bit followed by any number of ones: 0, 01, 011, 0111, and so on. The purpose of the padding field is to allow the length of the mantissa to be restricted so that only significant bits are present in the number; it acts as a substitute for unnormalization, which is not available for this purpose when extremely gradual underflow or overflow is in use, or when the first bit of the mantissa is hidden, as is the case in Comprehensive format. When neither Extremely Gradual Underflow nor Extremely Gradual Overflow is in effect, the Modified Native format is not required to permit unnormalized floating-point operation.
Note that Hyper-Gradual Overflow and Hyper-Gradual Underflow do not modify the form of the mantissa, do not affect unnormalized operation, and thus their presence in itself does not lead to a requirement for the Modified Comprehensive format. But because this also means that the Hyper-Gradual Overflow and Underflow principle could be applied to a floating-point format in which the leading one bit of the mantissa is suppressed, and this is taken advantage of in the Comprehensive format, a modification is still required in that format for unnormalization as well.
Because the Standard format does not use extremely gradual underflow, but only suppresses the first bit of the mantissa, it might seem that the easiest way to permit unnormalized operation with that format would be simply to stop suppressing the first bit of the mantissa. However, using a padding field with that format instead has several advantages:
It can be noted that when the modified versions of these formats are in use, so that the unnormalized floating-point instructions can be used, those instructions are not in fact performing unnormalized arithmetic, which remains incpmpatible with the formats as modified, but instead what is known as significance arithmetic. As a result, the Multiply Extensibly Unnormalized and Divide Extensibly Unnormalized instructions are not available with these modified formats.
It should also be noted that significance arithmetic, while it seeks to provide an indication of the accuracy of the final result of a computation, does so in only an approcimate fashion. Furthermore, when implemented by either of the means described here, by either the use of unnormalized values, or a padding field on the right of the mantissa, it increases the size of the rounding errors that take place in a calculation. Significance arithmetic, while it shares some of the goals of interval arithmetic, is not a substitute for it.
Also, note that the internal formats of numbers do not include complicated special features, and, in the cases where this is relevant, they have an extra range in the exponent field, and thus numbers in a special format with a padding field are represented by equivalent unnormalized numbers, with the appropriate number of guard bits, when within a floating-point register.
The Native floating-point format, when one or both of extremely gradual underflow and extremely gradual overflow are used, is significantly modified as follows if the bit indicating that the exponent and mantissa are to be inverted for negative numbers is used. This modification causes a slight increase in the range of representable numbers which can be stored. The modification described here does not apply to 128-bit floating-point numbers, for which extremely gradual underflow or overflow are not used.
When only extremely gradual underflow is used, the modified format consists of the following fields:
Rearranging the number in this way means that all numbers that are partly unnormalized are below the other numbers, according to their degree of unnormalization; this means that the property which is desired to be obtained by inverting the bits of a floating-point number when it is negative, collation as if the number were a two's complement integer, is achieved.
The extension of the numeric range results from the following change to the format: when the second field of the number, the first part of the mantissa, is so long that less than 11 bits remain in the number, then the exponent field is gradually shortened. This can continue right down to an exponent field of zero bits, which indicates the exponent value immediately below the lowest exponent indicated by an exponent field of one bit.
When the first part of the mantissa field contains all zeroes, then the remaining fields are not present, and the number represented is zero.
Incidentally, this kind of coding has already been actually used, as it forms the basis of the A-law encoding of audio signals.
When only extremely gradual overflow is used, one change is made to the format. The bits of the field containing the first part of the mantissa are inverted, so that this part of the mantissa may consist of 0, 10, 110, 1110, and so on. In this way, the less normalized numbers are larger than the fully normalized ones, which again leads to the numbers collating correctly.
When both extremely gradual underflow and extremely gradual overflow are present, then the native floating-point format is further modified, being divided into five fields instead of four:
Note that for negative numbers with positive exponents, the first part of the mantissa field will be negated twice.
Here is a small-scale illustration of the principle involved, with an exponent in excess-16 form instead of excess-1024 form, and only five significant bits maximum:
0 1 110 111 00 2^22 0 1 110 000 00 32,768 0 1 10 111 000 16,384 0 1 10 000 000 128 0 1 0 111 0000 64 0 1 0 001 0000 1 0 1 0 000 0000 .5 0 0 1 111 0000 .25 0 0 1 000 0000 2^(-9) 0 0 01 111 000 2^(-10) 0 0 01 000 000 2^(-17) 0 0 001 111 00 2^(-18) 0 0 001 000 00 2^(-25) 1 0 1 110 1111 -1
When a padding field is present at the end of the number, of the form 0, 01, 011, and so on, to permit unnormalized operation to indicate significance, which will be the case when the modified native format is indicated, that field, like the part of the mantissa after its first 1 bit, is inverted only when the number is negative.
In the case where extremely gradual overflow is present, whether alone or in combination with extremely gradual underflow, and NaN-safe operation is indicated, the maximum possible exponent value for which there are fifteen bits remaining in the mantissa field after its most significant one bit is the one which indicates a not-a-number value, and higher, less normalized positive exponents are not available. And where only extremely gradual underflow is present, the maximum exponent value in the case of the first part of the mantissa field having its minimum length will be the one indicating a not-a-number value.
The Comprehensive floating-point format can also be modified in this manner. Hyper-gradual overflow or underflow is simply a prefix-property encoding of the exponent field, and it is already collating, and requires no modification of the format. Thus, when hyper-gradual overflow is combined with extremely gradual underflow, for example, for positive exponents, the exponent field simply begins where only the first, zero, bit of the exponent is found for negative exponents.