The subdivided floating-point feature works in a modified fashion for each of the possible choices for data memory width control, and its description was placed in this section for that reason. This feature, on the other hand, works in only one way, and is fundamentally incompatible with data memory width control.
The general principle on which this feature is based is described on this page.
However, it is also described here because its function is related to that of both features. As well, data memory width control can still be in effect when this feature is used, as there are bits in the Program Status Block to indicate that data memory width control is to be ignored for those floating-point precisions with which this feature will be used. Note that this will normally require one or more base registers to be dedicated to the instructions that work with memory in a different way.
While the Data Memory Width Control mechanism provides an effective way for the computer to function as though it had a 36-bit or 48-bit word length, as well as other word lengths, it does so by making use of the cache, specifically the Level 2 cache.
When it is desired to use 36-bit or 40-bit single precision numbers, and 48-bit intermediate precision numbers, in conjunction with normal 64-bit double precision numbers, in very large arrays that will be randomly accessed, so that the cache will not be of assistance in handling those arrays, a different way of organizing data is required to avoid excessive overhead from fetching consecutive 256-bit memory words into the cache before the desired item can be accessed.
Thus, a scheme is used that avoids unaligned data that crosses 256-bit memory word boundaries, while also avoiding the need to divide addresses by odd numbers, as is required for subdivided floating-point operation.
Essentially, how it functions is as follows:
Memory is treated as divided into units of 256 bits. These units are divided into a power-of-two number of each of several different lengths of floating-point number. Even though the lengths of the numbers are lengths which do not involve a power-of-two number of bits, and they are packed together, they are addressed as if they were even subdivisions of the 256-bit memory unit.
Thus, for example, a 256-bit memory line can contain four 36-bit numbers as well as one 48-bit number and one 64-bit number. In this case, the 36-bit numbers would be accessed using single-precision floating-point instructions, but they would be addressed using addresses on 64-bit boundaries.
This makes it very simple and uncomplicated for a compiler to generate code to manipulate 36-bit numbers. The standard single-precision instructions would be used, but array arithmetic would be handled in the normal manner used for double-precision numbers: thus, subscript values would be shifted three places instead of two before being used as array indexes.
The space left unused by the 36-bit numbers contains one 64-bit number and one 48-bit number. They are accessed by double-precision and intermediate-precision instructions respectively, and they have the same addresses even though they occupy independent portions of storage, and can thus both be used simultaneously: they are given the address of the beginning of the 256-bit memory unit in which they are found. This is also the same address that the first of the four 36-bit numbers placed there has.
The mode settings that allow the memory to be used in this way also permit a 256-bit memory unit to instead be used for four 64-bit double-precision numbers in the ordinary way, or to instead be used for one 64-bit double-precision number, as above, and four 48-bit intermediate-precision numbers that appear to be spaced on 64-bit boundaries.
One can also choose to turn on the feature for the 48-bit numbers accessed in this way, without turning on the use of 36-bit numbers. In that case, single-precision instructions will instead treat a 256-bit memory unit normally as containing eight 32-bit single-precision numbers.
The intent is to provide as much flexibility in the use of memory for different floating-point precisions as possible, subject to the constraint that using some of a 256-bit memory unit for floating-point numbers of a given unconventional length will result in some space left over which is only usable for floating-point numbers of other specific lengths.
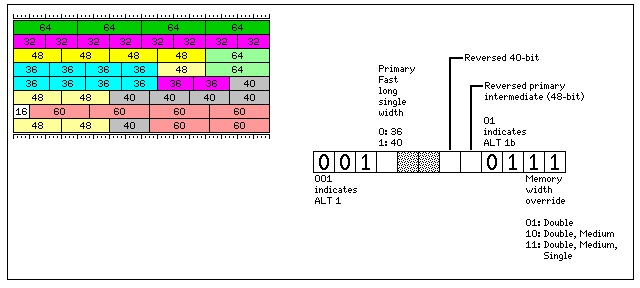
The Fast Intermediate mode locates four 48-bit floating-point numbers at the end of a 256-bit memory word, but addresses them as if they were 64-bit data items distributed normally in the 256-bit memory word.
The Fast Long Single mode will either locate four 36-bit floating-point numbers at the end of a 256-bit memory word, or four 40-bit floating-point numbers at the beginning of a 256-bit memory word. In either case, these four numbers will also be addressed as if they were 64-bit data items distributed normally in the 256-bit memory word.
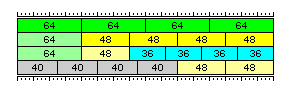
The following diagram illustrates how these modes can be used in conjunction to permit efficient use of memory if an appropriate mix of lengths of floating-point data is available:

Placing the 48-bit numbers and the 36-bit numbers at the end of the end of a 256-bit memory word facilitates intermixing of 48-bit intermediate precision numbers with 64-bit double precision numbers, since the 64-bit double precision number in the left-over space is aligned at the beginning of a 256-bit memory word, and thus can be addressed as if it were an aligned 256-bit object. Similarly, it facilitates intermixing 36-bit single precision numbers with both 48-bit intermediate precision numbers and 64-bit double precision numbers, since now both the 48-bit number and the 64-bit number in the left-over space have the same address, aligned at the beginning of the 256-bit memory word that contains them.
The modes shown in the first three rows of the diagram above interact as follows:
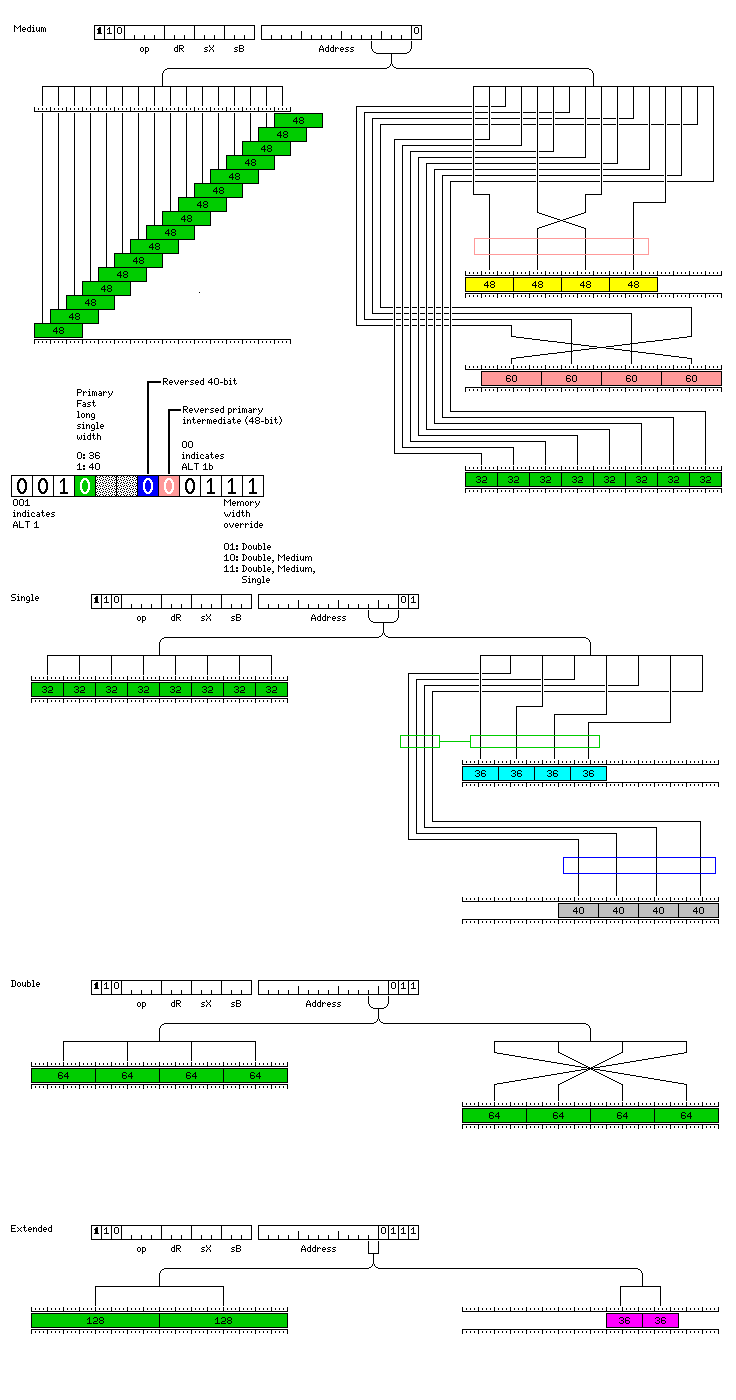
If only fast intermediate is turned on, then any 256-bit memory line can be used efficiently in one of three ways:
As four 64-bit double-precision numbers, aligned on 64-bit boundaries.
As one 64-bit double-precision number, aligned on 256-bit boundaries, and four 48-bit intermediate-precision numbers, which will appear to the program to be aligned on 64-bit boundaries.
As eight 32-bit single-precision numbers, aligned on 32-bit boundaries.
When both fast long single and fast intermediate are turned on, then any 256-bit memory line can be used efficiently in one of these three ways:
As four 64-bit double-precision numbers, aligned on 64-bit boundaries.
As one 64-bit double-precision number, aligned on 256-bit boundaries, and four 48-bit intermediate-precision numbers, which will appear to the program to be aligned on 64-bit boundaries.
As one 64-bit double-precision number, aligned on 256-bit boundaries, one 48-bit intermediate-precision number, appearing to the program to be aligned on 256-bit boundaries, and four 36-bit single-precision numbers, appearing to the program to be aligned on 64-bit boundaries.
In order to permit 40-bit single precision numbers and 48-bit intermediate precision numbers to be intermixed, when both fast long single mode and fast intermediate mode are selected, and the length for fast long single mode is set to 40, it is advised to also turn on both interleaved floating-point addressing and reversed floating-point addressing, at least for the intermediate precision numbers. (The ability to turn these features on for long single-precision numbers as well, and to turn either feature on or off separately, have been provided in the event it might become useful if this feature is extended in future to allow handling of other data widths.)
Interleaved floating-point addressing causes four data items stored by means of this form of addressing to be stored in the order 0, 2, 1, 3 instead of the order 0, 1, 2, 3. Using that feature alone will cause the left-over 48-bit floating-point numbers at the end of each 256-bit memory word to appear to be spaced uniformly at 128-bit intervals, but they will be 64-bit items occupying the last half of an aligned 128-bit object.
Reversed floating-point addressing causes four data items stored by this form of addressing to be in the order 3, 2, 1, 0; when combined with interleaved floating-point addressing, the order becomes 3, 1, 2, 0. In that way, two 48-bit floating-point numbers at the end of each 256-bit memory word can be addressed as though they were 128 bits long.
With the settings descrbed here, there are also three available ways to use each 256-bit memory line:
As four 64-bit double-precision numbers, aligned on 64-bit boundaries.
As one 64-bit double-precision number, aligned on 256-bit boundaries, and four 48-bit intermediate-precision numbers, which will appear to the program to be aligned on 64-bit boundaries.
As four 40-bit single-precision numbers, appearing to the program to be aligned on 64-bit boundaries, and two 48-bit intermediate-precision numbers, appearing to the program to be aligned on 128-bit boundaries.
Note that the modifications to how memory is seen caused by Fast Intermediate and Fast Long Single modes, as well as by interleaving used with either mode, only affect floating-point instructions acting on operands of the appplicable width, precision, and type, and not any other instructions which address memory. Also, note that the bit indicating Fast Long Single mode must be set for the bit indicating Interleaved Fast Long Single mode to cause interleaving for single-precision floating point operands, and the same applies to the bits for Fast Intermediate mode and Interleaved Fast Intermediate mode.
Because these modes depend on the ability to use floating-point numbers of related sizes, in order to avoid unused memory being left in each 256-bit unit of memory, they are not compatible with Data Memory Width control. This feature may, however, be turned on along with this one, so that some data types will be addressed according to the technique of Data Memory Width control, while those intended to be used with this technique ignore it.
This is determined by the Program Status Block (PSB) bits marked Data Memory Width Control override. When they are set to include certain types, the Subdivided Floating features described on the previous page are also overriden if set.
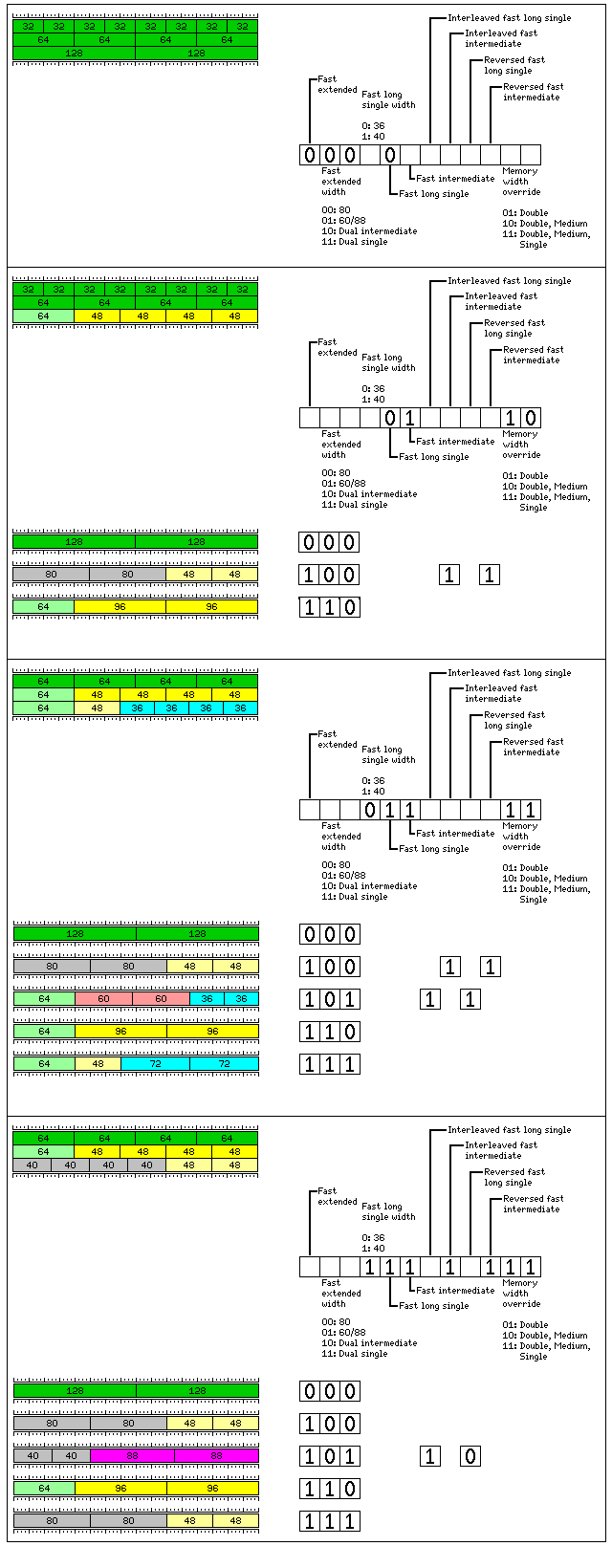
Additional possibilities exist which, in some cases, require extending the model. While the benefits of using 60-bit double-precision numbers instead of 64-bit double-precision numbers are limited, they can be mixed with 36-bit floating-point numbers, and so this option is provided as well.
The first three rows show how floating point numbers are stored in normal operation, with eight 32-bit single-precision numbers, four 64-bit double-precision numbers, or two 128-bit extended precision numbers in a 256-bit memory line.
The fourth and fifth rows show how the simplest case of fast long intermediate mode, placing four 48-bit numbers in the same 256-bit word memory line, is compatible with two 96-bit extended precision numbers being placed there as well.
The sixth row shows a case involving two different forms of double-precision numbers, one 64-bit double-precision number and two 60-bit double-precision numbers, as well as two 36-bit single-precision numbers.
If these are the three types in use, making them all accessible might appear to be simplest by accessing the 60-bit type by the use of the intermediate-precision floating-point instructions. In fact, though, given the 64-bit number at the beginning of the 256-bit memory line, and the two 36-bit numbers at its end, this arrangement clearly has overlap with that containing four 36-bit numbers and one intermediate-precision 48-bit number. Thus, it would be desirable to allow simultaneous use of that precision as well.
Therefore, 60-bit precision has been set up as a case of extended precision. When the appropriate extended precision option is chosen, extended precision instructions referencing the first and last 128 bits of a 256-bit memory line instead refer to the two 60-bit floating-point numbers in the positions shown in the diagram. By using reversed and interlaced addressing for the fast long single 36-bit numbers, the same settings now allow (64)(60)(60)(36)(36) and the series of (64)(64)(64)(64), (64)(48)(48)(48)(48), and (64)(48)(36)(36)(36)(36).
Just as two cells, each containing one 64-bit double-precision number, can be used for one 128-bit extended-precision number, the case with 40-bit single-precision numbers is compatible with 80-bit floating-point numbers; as those, normally, are aligned on 16-bit boundaries, they were usually accessed as intermediate-precision numbers. In this case, as that would conflict with accessing the 48-bit floating-point numbers, they are referenced by extended-precision floating-point instructions when indicated by the dual single setting of the Fast Extended bits in the Program Status Block.
The same mechanism can be used to build 80-bit numbers from 40-bit numbers as to build 72-bit numbers from 36-bit numbers: use the extended precision instructions to access these numbers.
Thus, when fast long intermediate is on, but fast long single is off, two intermediate-precision numbers become an extended-precision number; this allows 96-bit extended precision floats to be accessed. When both fast long intermediate and fast long single are on, as there will be four single-precision numbers in a 256-bit memory line, but only one word of other lengths, extended-precision instructions access either an 80-bit extended precision number or a 72-bit double precision number.
This takes care of those cases without modifying the Program Status Block.
The two 36-bit single-precision floating-point numbers left over when 60-bit precision is present can be made evenly spaced through the use of interleaved floating-point addressing. In order that they are in 64-bit positions 2 and 0 instead of 1 and 3, it is necessary to use reversed floating-point addressing as well.
Thus, it becomes clear what must be added for this case. The Fast Long Intermediate width must be modifiable from 48 bits to 60 bits, and interleaved (but not reversed) floating-point addressing will be used for the Fast Long Intermediate data.
As well, memory width override must be separately controllable for extended precision.
The principal useful combinations of the possible settings are shown in the diagram below, which shows in each section (except the first, for which only one setting for extended precision is applicable) one value of the settings for the precisions other than extended precision with the possible settings for extended precision grouped below that value:
For both Fast Intermediate and Fast Long Single numbers, interleaved and reversed addressing, when enabled or disabled, lead to the four numbers of that type within a 256-bit memory line being addressed as follows:
Interleaved Reversed Off Off nn00 nn08 nn10 nn18 On Off nn00 nn10 nn08 nn18 Off On nn18 nn10 nn08 nn00 On On nn18 nn08 nn10 nn00
This is why interleaved addressing is used when the first two of four items of a given type are the only ones available in a 256-bit memory word, the other storage being used for items of other types, and reversed addressing is used when only the last item remains, and reversed and interleaved addressing are used when only the last two remain. As well, it is clear why neither is needed when it is only the first one that remains.
Note that these modes don't enforce accessing the portions of the 256-bit memory line in the manner shown. Thus, as we've seen above, a 256-bit memory line, under the settings providing for four 36-bit numbers, can instead be accessed as containing four 48-bit numbers instead of one, or as containing four 64-bit numbers instead of one.
Also, for example, when the word is shown as divided into a 64-bit word, two 60-bit words, and two 36-bit words, one can access four 36-bit words on 64-bit boundaries instead of two 36-bit words on 128-bit boundaries; the result will be wasting some of the space that could be used for two 60-bit words instead of two 36-bit words.
The starting points for 36-bit fast long single as against 40-bit fast long single, and for both 48-bit fast intermediate and 60-bit fast intermediate are implicit and fixed.
As well, note that memory width override is used for double precision, even though its length is not modified by the fast long single, fast intermediate, or fast extended modes. This is in order to ensure that double precision continues to act conventionally, so that it can be used to access the left-over space in a 256-bit memory unit. In this way, a program that accesses a limited amount of character or fixed-point data which does fit in cache may use data memory width control so that this data can be of an unconventional length, while using this feature instead to facilitate alternate lengths of floating-point data which is in large arrays that will not make optimal use of cache.
| Memory width override can be used even when neither the fast intermediate nor the fast long single feature is used, to allow floating-point data to have conventional lengths and organzation in storage while other forms of data are modified by data memory width control. |
When memory width override is on for floating-point instructions associated with a given precision, if both subdivided and fast operation are set for it, fast takes precedence; when memory width override is not on, subdivided takes precedence.
Note that memory width override is not explicitly specified for Extended Precision instructions. For this mode, when memory width override applies to Extended Precision instructions is determined by the width chosen for them:
80 if Intermediate 10 11 60/88 if Single 11 Dual Intermediate if Intermediate 10 11 Dual Single if Single 11
Thus, if Dual Intermediate is chosen as the width for Extended Precision numbers, then memory width override applies to them if either Double and Medium or Double, Medium, and Single are selected as having memory width override.
Also note that if little-endian operation is selected, the positions of floating-point numbers, within the 256-bit memory unit, and their addressing, do not change; only the contents of the storage allocated to a floating-point number will change. However, if little-endian operation is implemented by inverting a varying number of low-order address bits, the physical positions of floating-point numbers may be changed.
If Fast Extended is turned off, it is not relevant to specify the width of Fast Extended numbers. This leads to bit combinations which are not required which can be used for future expansion. Some of them are used to specify a mode where four 60-bit numbers, instead of just two of them, may be placed in a 256-bit memory line, as follows:
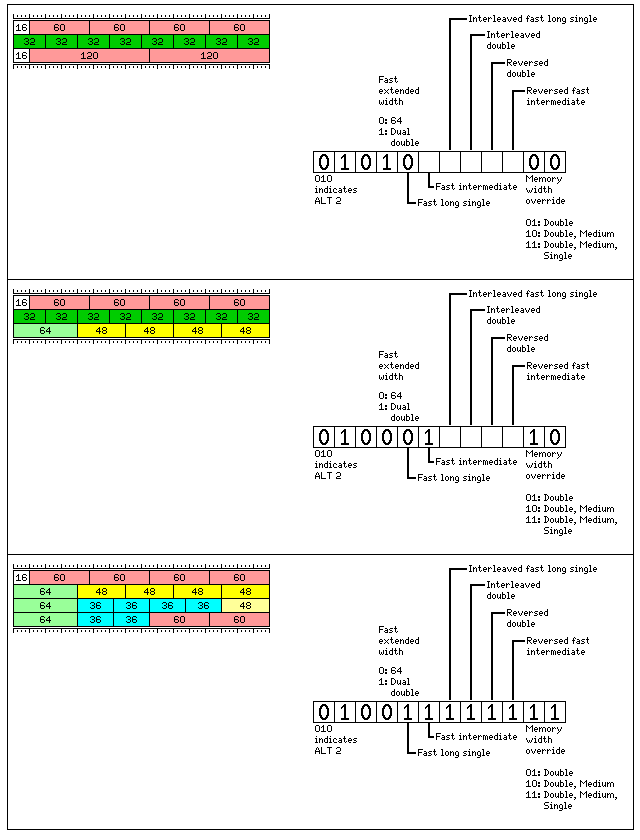
Here some of the elements within a 256-bit memory word are rearranged.
Just as in the modes in the previous diagram, a single 64-bit floating-point number was always located at the beginning of a 256-bit memory word, so that it could be accessed with unmodified double-precision instructions, here the left-over storage for a 16-bit fixed-point number is always located at the beginning of the 256-bit memory word so that it can be accessed with unmodified halfword instructions.
Here, Fast Double is now present, and it is always on in these modes. Fast Extended is also always on, and extended precision instructions either refer to 120-bit extended precision numbers, or to the one 64-bit double-precision number left in what would otherwise be unused space in the 256-bit memory word.
In this mode, Memory Width Override is turned on for Extended Precision when it is turned on for Double Precision.
As Fast Long Single numbers are always 36 bits long in this mode, and their addressing may be interlaced but never reversed, while the addressing of Fast Intermediate numbers may be reversed, but never needs to be interlaced, some bits in this part of the Program Status Block are available for reassignment to control the behavior of Fast Double numbers. Note also that the effects of interleaved and reversed addressing are identical for Fast Double numbers as for the other two types to which they have been applied here.
The prefix 011 is reserved for a mode very similar to the one shown here, except that Fast Long Single numbers are 40 bits in length, and therefore Fast Double numbers are reduced to 56 bits in length.
The space which contains four 60-bit floating-point numbers can also contain five 48-bit floating-point numbers.
The prefix 001 is used for a mode which allows this fact to be exploited.
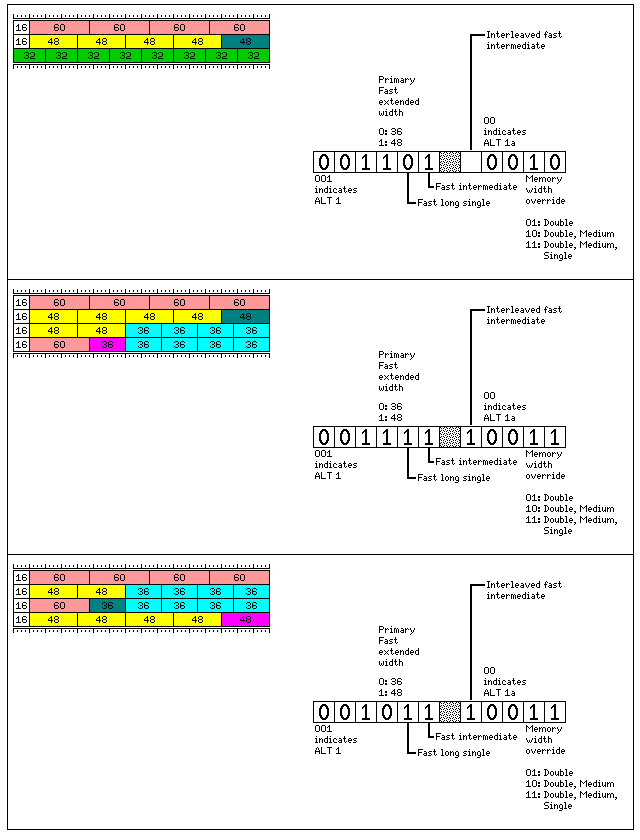
Here, double-precision instructions once again access the four 60-bit floating-point numbers in a 256-bit memory word.
In the first two of the three cases shown, intermediate-precision instructions access the first four 48-bit floating-point numbers in a 256-bit memory word, and extended-precision instructions access the fifth 48-bit floating-point number in a 256-bit memory word.
In the second case, single-precision instructions access the last four 36-bit floating-point numbers in a 256-bit memory word, and extended-precision instructions the addresses of which are odd multiples of sixteen bytes (or 128 bits) access the first 36-bit floating-point number in a 256-bit memory word.
It may seem odd that such an expedient was resorted to merely to allow a case in which five, rather than four, 36-bit floating-point numbers may be placed in a 256-bit memory word.
However, the third case illustrates the reason why this expedient was seen as necessary.
Here, extended-precision instructions with normal addresses, multiples of the basic 256-bit unit, are used to access the first of five 36-bit floating-point numbers in a 256-bit memory word.
Without the option of using the intermediate addresses of odd multiples of sixteen bytes to indicate operations on the fifth 48-bit floating-point number in a 256-bit memory word, the maximum number of 48-bit floating-point numbers that could be placed in such a word would be two.
In this mode, memory width override applies to Extended Precision instructions under the following conditions, based on their width:
64 if Intermediate 10 11 Dual Double if Double 01 10 11
Note, as well, that memory width override is applied by the type of instruction used to access a given type of floating-point number, and not by its actual width. This is significant in this mode, since the Extended Precision instructions can be used to access either a single-precision 36-bit floating-point number, or an intermediate precision 48-bit floating-point number.
Using addresses for intervening extended-precision numbers illustrates a principle which can be taken further. Since intermediate-precision numbers are aligned to 16 bit boundaries, there are a significant number of aligned addresses available for use to address alternate floating-point operand lengths in this fashion.
A mode which takes advantage of this to offer greater flexibility in making use of the space in a 256-bit memory word is illustrated below:
The four 64-bit elements are always addressed as double-precision numbers, but in reverse order:
18 10 08 00
The four 48-bit elements are always addressed as the four principal intermediate-precision numbers, and are always addressed with interleaved addressing, but they may or may not be addressed with with reversed addressing, depending on whether use with 40-bit numbers, or use with 36-bit and 64-bit numbers is to be emphasized:
00 10 08 10 18 08 10 00
The four 60-bit elements are always addressed as the four secondary intermediate-precision numbers, with interleaved and reversed addressing:
1C 0C 14 04
The eight 32-bit elements are always addressed as the eight ternary intermediate-precision numbers, and with addresses in normal order:
02 06 0A 0E 12 16 1A 1E
The first four 36-bit elements are always addressed normally, but they may be the four principal single-precision numbers, or the four secondary single-precision numbers:
00 08 10 18 04 0C 14 1C
The four 40-bit elements may be addressed with reversed addressing, if operation with 36-bit numbers is emphasized, or normally if operation with 48-bit and 60-bit numbers is emphasized. Also, they may be the four secondary single-precision numbers or the four principal single-precision numbers:
1C 14 0C 04 04 0C 14 1C 18 10 08 00 00 08 10 18
The final two 36-bit elements, when the maximum of six 36-bit elements are present in a 256-bit memory word, are addressed as the two possible aligned numbers in such a word reachable by an extended-precision instruction:
00 10
Note that the hexadecimal values relate to the address position from which mapping takes place, and so do the positions of the numbers, which may make the tables above somewhat confusing, as they are mixing items that point in opposite directions.
In this mode, memory width override applies to the operands of Extended Precision instructions (which are 36-bit single precision numbers) if it is selected for single precision numbers, since these numbers, the two additional 36-bit numbers, are used with 36-bit and 40-bit numbers, both accessed by the single precision instructions.
As this mode is somewhat complicated, it may be helpful to illustrate how the floating-point numbers usually referenced by floating-point instructions are mapped to those of alternate lengths in this mode in an explicit fashion.
The red and blue boxes show where the mapping to floating point numbers would be reversed if those PSB bits highlighted in the respective colors were 1; the pair of green boxes joined by a line shows where the mappings of two groups of numbers would be switched if the PSB bit highlighted in green was a 1.
This mode allows the use of a large number of different lengths, by exploiting the fact that 16-bit alignment means that there are many possible valid addresses for an intermediate precision number available.
In order to allow the use of 48-bit intermediate precision numbers, two lengths of double-precision numbers, and two lengths of single-precision numbers, however, note that while extended precision instructions are used, no actual extended precision numbers are addressable in this mode. This is one reason why, although this mode may seem to be a superset of the ones described earlier on this page, one of the other forms of Fast Intermediate and Fast Long Single addressing may be preferred instead for a given program.