We have seen in the previous pages the seemingly contradictory conditions which need to be fulfilled for a computer to work efficiently on floating point numbers the lengths of which are not related to one another as simple power-of-two multiples.
On the one hand, efficiency requires that these data items all fit evenly into a single memory word, so that it is never necessary to fetch two consecutive memory words to obtain a data item that is aligned badly.
On the other hand, it is simple to convert addresses from one form to another by multiplication, but not by division.
Thus, the first consideration suggests using aliquot parts of a memory word other than powers of two, dividing it into three or five equal parts, for example, and the second consideration forbids this strategy.
In the previous page called Almost Sane Addressing, it was noted that if one does not insist on always using memory with 100% efficiency, an option exists to pack data items of different widths into a memory word.
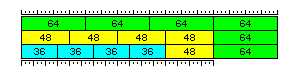
Here is an illustration of how that principle can be applied very simply to a 256-bit memory word (thus allowing this to be done with a computer that has conventional memory hardware and conventional data types) to satisfy these two seemingly contradictory conditions:

Double-precision floating-point numbers are left as 64 bits, rather than being shortened to 60 bits.
Each 256 bits of memory can contain four 64-bit double precision floating-point numbers in a conventional fashion.
It can also contain four 48-bit intermediate precision floating-point numbers. Since four of them, rather than five, are placed in 256 bits of memory, no attempt to divide by five when addressing is required; they can be addressed as if they were 64-bit floating point numbers, and converting the value in the index register to what is actually required to fetch a 48-bit array element is trivial.
Treating the one 64-bit number present as though it were 256 bits long for purposes of indexing only requires a shift; as this sort of thing is done normally when setting up for indexing, because an index could refer to an 8-bit character, a 16-bit or 32-bit integer or a 32-bit or 64-bit float, it isn't even necessary to have a special instruction or a special addressing mode to deal with this.
And it can also contain four 36-bit single precision floating-point numbers, one 48-bit intermediate precision floating-point number, and one 64-bit double precision floating-point number.
The 48-bit floating-point number, which was treated as 64 bits long, now has to be treated as 256 bits long - so its address only needs to be shifted two bits to the left. Again, no additional instruction or addressing mode is required.
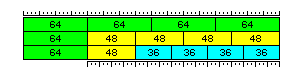
Actually, it is probably better to implement this scheme with the order of elements in memory reversed, as depicted above. In this way, the left-over 64-bit element when memory is used for 48-bit numbers is at the position referenced normally by addresses which end in extra zeroes, being on 256-bit boundaries; and the same is true for the left-over 48-bit element when memory is used for 36-bit numbers, since addresses of 48-bit numbers will reference whatever part of the 256-bit unit is used to store them - and so left-aligning these numbers does not serve the purpose of keeping addressing simple, as there is a tendency to assume instinctively.
One complexity, though, that has been glossed over here is that individual 36-bit floating-point numbers would be aligned on four-bit boundaries, and a computer with conventional data types and addressing normally can only address data on eight-bit boundaries. One option for dealing with this would be to use 40-bit single precision floating-point numbers instead of 36-bit single precision floating-point numbers. Four of those, and two 48-bit intermediate precision floating-point numbers (again, just as four and one are both powers of two, so are four and two) will evenly fill a 256-bit memory word.
However, this does not need to be a concern. The techniques discussed here are intended for use in cases where very large arrays of these types are being handled. Small arrays that can fit in cache can instead be handled by the technique described here, which involves partially filled cache lines which then are handled by internal circuitry so as to allow fully packed items of most desirable lengths.
In addition, instead of only modifying the index register contents before indexing them, the required addressing modification can be applied to the sum of the index and the displacement, thus fixing the alignment, at least relative to base register contents, of the 256-bit memory words in which the items are located; in which case the 36-bit operands will be addressable without indexing as if they were 64-bit operands.
On this page, under the name "fast long single" and "fast intermediate" floating-point, in the context of an illustrative computer architecture, a possible implementation of this type of memory organization in this fashion is illustrated. Interleaving of 48-bit operands and locating 40-bit operands at the end of the block allow multiple instructions and complicated index calculations to be avoided.
Although storing only four 36-bit single precision floats in 256 bits, and trusting to it being possible to store other data in the unused space, is far from ideal, this scheme does provide reasonable handling of data of these unconventional lengths in a fashion that is efficient as far as speed, as opposed to RAM utilization, is concerned.
Incidentally, this principle can also be applied to computers of other word lengths. Thus, instead of starting from the 8-bit byte and the 32-bit word, one can instead look at what can be done for a computer with a 24-bit or 48-bit word length:
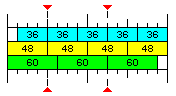
If we take a 192-bit memory bus, that consists of sixteen units of 12 bits. That comprises four 48-bit intermediate-precision floating-point numbers. If one leaves 12 bits unused, fifteen units can correspond to either three 60-bit double-precision numbers, or five 36-bit single-precision numbers.
Using the principle shown here, as can be seen from the diagram, a 192-bit memory word can be divided into either one 48-bit number and four 36-bit numbers, or two 60-bit numbers and two 36-bit numbers.
We met this diagram before on the page Almost Sane Addressing. There, it was proposed to allow an odd number of floating-point numbers of a given size within a memory word by addressing by columns instead of rows.
Here, instead, the same division of the memory word is combined with addressing by rows, using power-of-two groups of numbers of the same size as the unit of addressing. An odd number can still be used, as the sum of two powers of two; in that case, arrays with less of a requirement for optimal use of the cache would use the smaller power.