
As noted on the previous page, dividing memory into units 12 bits in length allows for floating-point numbers of sizes that seem to be particularly useful: single precision numbers 36 bits long, which were found to be useful in many cases where 32 bits was not enough; intermediate precision numbers 48 bits long, which correspond well to what had traditionally been felt to cover most needs, as implemented on many pocket calculators, for example, as well as a number of early scientific computers; and double precision numbers 60 bits in length, which would not suffer from being shortened, as the precision of 64-bit double precision numbers is almost always more than is needed.
A high-performance design might involve the use of standard memory parts which are 128 bits wide. This could be used for 120 bits of data, and 8 bits of ECC, thus avoiding the premium prices of the less commonly used memory parts which are 72 or 144 bits wide to provide for ECC with conventional 64 and 128 bit buses.
However, current standard memory parts are 64 bits wide, leading to the temptation to connect three of them across to the chip to match the alignment of all the data types except for the last few bits of the address... leading to the need to do two fetches (in at least some cases) just to check the ECC. Also, it may not be so much the extra 8 bits of width for ECC as the internal buffering for "registered" RAM that leads to some memory parts being quite a bit more expensive.
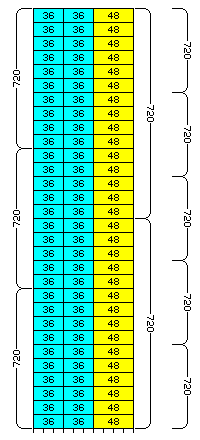
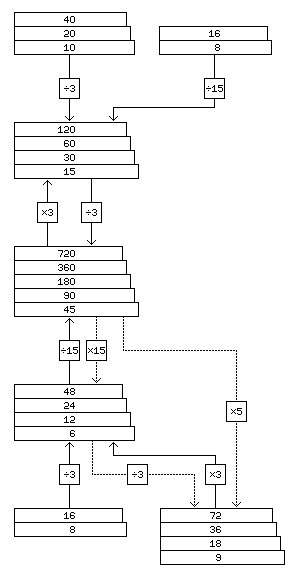
Fetching six 120-bit memory words into cache at once establishes a 720-bit unit which can contain an even number of fully-aligned data elements of all these sizes; 20 36-bit single-precision floats, 15 48-bit medium-precision floats, and 12 60-bit double-precision floats.
This diagram shows how 120-bit memory words, organized into 720-bit memory blocks, conveniently accomodate aligned 36-bit, 48-bit, and 60-bit floating-point numbers:

One 120-bit word contains two 60-bit floating-point numbers; two 120-bit words contain five 48-bit floating-point numbers, and three 120-bit words contain ten 36-bit floating-point numbers, and thus six 120-bit words are composed of an integral number of elements of all three sizes.
The internal extended-precision floating-point format could be 120 bits long, so as to fit most simply with the memory architecture. However, another issue is raised. While aligned 36-bit and 48-bit floats would work well when fetched from internal L2 cache, alignment would not yield the benefit of always avoiding a double memory fetch in situations where numbers were not obtained from the cache. This would be likely to take place in calculations which involved very large arrays, which are not uncommon in scientific computation.
To address this issue, it is proposed that an additional floating-point type be introduced, 40 bits in length. The exponent would be the same size as that for the 48-bit floating-point number, which would mean that while only two bits of precision would be gained from the 36-bit single-precision floating-point number, the exponent range would be significantly increased, reducing the chance of running into overflows or underflows during large-scale computations.
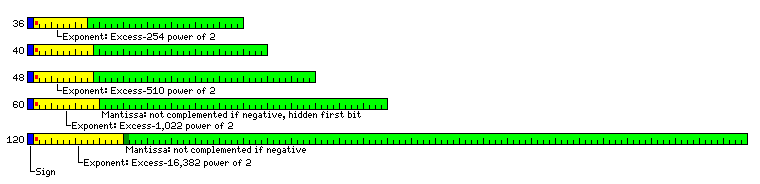
As the 32-bit IEEE 754 floating-point format has an exponent field the same width as that of the IBM 7090 floating-point format, expanding this format to 36 bits provides one additional bit of precision compared to that format, due to the hidden first bit of the mantissa. Since the precision provided by the IBM 7090 is considered adequate for a single-precision number, but the exponent range is very restricted, it would seem appropriate to allocate one extra bit to the exponent. In this way, the precision matches that of the IBM 7090, and the exponent range approximately matches that of the IBM 360.
In a 48-bit floating-point number, eleven bits were allocated to the signed exponent, one less than in the 60-bit floating-point number, or in 64-bit floating-point numbers in the IEEE 754 standard, so as to allow the maximum possible precision for the number while ensuring that the exponent range allows an exponent range that exceeds one from 10-99 to 10+99. However, this choice may be problematic; while it matches what is provided by many decimal calculating devices, it provides two additional bits of precision, but one less bit of exponent, than the floating-point format of the Control Data 1604 computer. (The 60-bit format approximately matches the 6600 in exponent range, but has one more bit of precision.) Thus, it may be appropriate to sacrifice one bit of precision in the 48-bit and 40-bit floating-point formats to better achieve a major goal of this design: better transportability of programs which performed massive floating-point calculations which were originally written for older computers serving that purpose. With the hidden first bit, the precision of 48-bit floating-point numbers, even after the loss of one bit of precision, would be 37 bits, equivalent to 11 decimal digits.
The ranges of the various floating-point formats provided are:
36 bit
with full precision
-77 77
6.9089 * 10 to 1.1579 * 10
-253 256
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to
-85
5.1476 * 2
-279
( 0.5 * 2 )
40 bit and 48 bit
with full precision
-154 154
2.9833 * 2 to 1.3408 * 10
-509 512
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to
40 bit
-163
5.5569 * 10
-538
( 0.5 * 2 )
48 bit
-166
1.3567 * 10
-550
( 0.5 * 2 )
60 bit
with full precision
-308 308
2.2164 * 10 to 1.7977 * 10
-1,021 1,024
( 0.5 * 2 to 0.9999... * 2 )
with reduced precision, down to
-322
1.5810 * 10
-1,069
( 0.5 * 2 )
120 bit
with full precision (gradual underflow not included)
-4,933 4,931
8.4053 * 10 to 5.9487 * 10
-16,383 16,383
( 0.5 * 2 to 0.9999... * 2 )
The 120-bit word length provides a large choice of fundamental units into which it can be divided. To allow a simple and powerful instruction format, it is proposed that the basic unit of an instruction should be 20 bits in length.

In this way, the first unit of an instruction can reference registers from groups of 32 registers, thus allowing most operations to take place in a register-to-register fashion, as the number of registers would be comparable to that used in many RISC designs. Given a 20-bit unit, three bits to indicate a base register, and a 17-bit displacement, would allow the base register field to be placed with the displacement, as on the IBM 360 architecture, without having base registers point to small areas of only 4,096 bytes as is the case there.
At this point, a major design decision is faced. All the data types align on 720 bit boundaries. But the simplest external memory connection is to a data bus that is 120 bits wide. 720 is six times 120, and six includes a factor of three.
Should base register values, and the main part of an address, be internally in terms of 120-bit (or 15-bit) units, so as to avoid having to multiply them by three to get the actual memory address to use externally in the memory interface, or would this introduce an implementation-dependent element in the architecture that would interfere with future expansion to, say, an external 360-bit data bus?
Since it is much easier to multiply by three than it is to divide by three, keeping the architecture clean, even if the prospect of moving to a 360-bit data bus in the future seems distant, would seem appropriate. In any case, the base registers could be implemented so that the multiplication takes place when they are loaded - that is, they could be shadowed by a register containing three times their value. However, a reason for using a 120 bit unit instead will become apparent in the next step.
Thus, the base registers will be defined as pointing to 720-bit units in memory. Given that 64-bit addressing is becoming the current standard, and that this standard is a generous one, external address buses being 45 or 48 bits, it seems to be appropriate to define the base registers as being 60 bits wide.
For normal computation, 30-bit general registers seem to be adequate for most arithmetic involving binary integers. Instead of having a "64-bit mode", having separate instructions for 60-bit arithmetic on a pair of registers, and a mode bit to specify 60-bit indexing instead of 30-bit indexing would appear sufficient. Switching from 30-bit to 60-bit base registers, or having 45-bit base registers, seems like an unnecessary complication to introduce.
The next step is to deal with the format of the address field of an instruction. It is envisaged that the architecture will be able to handle the following data types:
Type Bits length Unit In 120 bits In 720 bits
Characters
6 6 20 120
8 8 15 90
9 9 -- 80
10 10 12 72
12 12 (6?) 10 60
15 15 8 48
16 16 (8?) -- 45
30 15 4 24
Binary Integers
30 15 4 24
60 15 2 12
Floating-point Numbers
36 12/9 -- 20
40 10 3 18
48 12/16 -- 15
60 12/15/10 2 12
120 12/15/10 1 6
Decimal
Packed Decimal 4 12 30 180
Compressed Decimal 10 10 12 72
Instructions
20 10 6 36
To make address arithmetic as efficient as possible, the displacement field in an instruction should be divided into two parts; a binary part indicating a fixed-width unit in memory, and a part indicating which portion of that unit is being addressed. Note, though, that while the various types of item listed above largely fit into a division of memory into units of either 12 bits or 15 bits, with a 10 bit unit also important, there are no data types based on the 45-bit unit. Thus, while making the binary portion of a displacement refer to 720-bit units would require a non-binary portion to all displacements, making the binary portion of a displacement refer to the 120-bit unit would allow items which fit into the scheme of a 15-bit unit to have pure binary displacements.
And this would suggest that while a 40-bit floating-point type would be highly efficient for fetching when the data bus is 120 bits wide, later, when it is expanded to 360 bits, a 45-bit floating-point type would be more appropriate, since it would then permit the most efficient addressing. And that seems like a needless complication. Thus, the temptation is strong at this stage to make the initial implementation detail of a 120-bit data bus a permanent part of the architecture, so that there is at least one simple, normal, native addressing mode.
If, however, we remain resolute, and note that having all addresses treated in the same fashion is not a needless complication, we find that the smallest subdivision of a 720-bit unit required for addressing is the 6 bit character. Historically, 6 bit characters were all that was considered needed for simple computer applications. However, currently, almost no applications avoid the use of lower-case characters.
If 6 bit characters are not used, but 8 bit characters are, a small subdivision of memory used only for character data is still required, and this is also true in the case of 9 bit characters. On the other hand, if the smallest character size allowed was the 10 bit character, this unit, allowing both 30-bit integers and 40-bit floats to be referenced within the same system, is one valuable for handling larger words of data without an additional binary subdivision.
It seems obvious that the 9-bit character should be dispensed with, as this would require an additional unique configuration of the displacement field required for that type only.
Since 8-bit characters are very common in the general data processing world, and the Basic Multilingual Plane of Unicode is accessible with 16-bit characters, it would seem like there is a need to accomodate them, despite this requiring an addressing unit only required for character data.
While 6-bit characters are relatively easy to accomodate within the framework of the necessary 12-bit unit, they are likely to be almost completely unused.
A 17-bit displacement field, then, appears to have to be divided into a 10-bit field indicating a 720 bit wide unit of memory, and a 7-bit field indicating the required element of that field, since a unit of 10 bits, which occurs 72 times in 720 bits, has not been eliminated by the discussion above. Given that, the displacement format is adequate to accomodate the 6-bit character, and no savings results from eliminating it.
The following schemes for displacements suggest themselves; the second appears to lead to the simplest internal logic, whereas the third retains binary addressing for as long as possible:
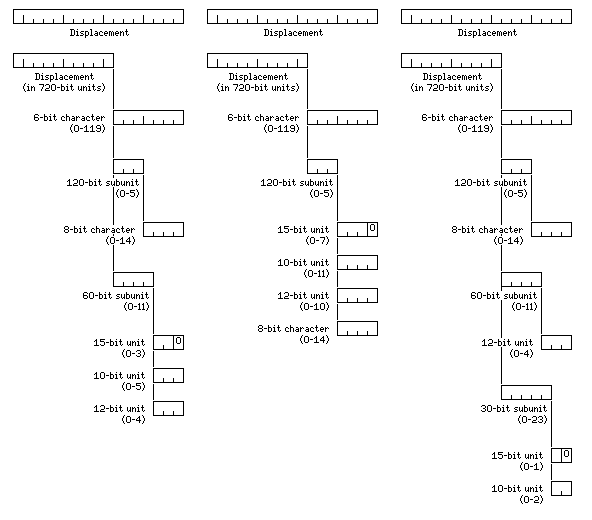
However, the question of how to represent the displacement field is essentially trivial.
It is, rather, the question of how to deal with indexing which brings us face-to-face with the difficulties inherent in a subdivision of memory not based upon a single common unit.
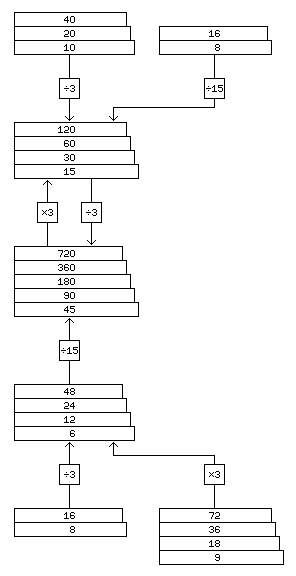
In the case of a computer with a 24-bit or 48-bit word length, if it was desired to make both 12-bit objects, and 8-bit characters directly indexable, this could be done by having the index register or registers, when used with 8-bit characters, represent a byte displacement, with that displacement being internally divided by three to obtain a displacement in memory words, with the remainder used to select the portion of the word to use. What will be illustrated here is how this can be further generalized to make use of the versatility inherent in a 720-bit block of memory.
While the displacement field in an instruction can be divided into two fields in order to allow more rapid address arithmetic, to properly obtain the benefits of indexed addressing, the contents of the index register must be a simple integer, giving displacements in one basic unit, such as a word or byte. Thus, to simplify addressing logic, the number of required addressing units must be reduced as far as is reasonable.
One option would be to reduce the number of addressing units as far as possible, to one, by addressing storage by individual bits. This, however, is better suited to conventional memory schemes, in which word lengths are powers of two.
Originally, the shift to a different memory width was intended to facilitate the use of 36-bit, 48-bit, and 60-bit floating-point numbers. A 12-bit unit is common to all of those widths.
However, since a 120-bit bus to main memory was envisaged, an additional efficient 40-bit floating-point format was added, the normal width of fixed-point numbers was set at 30 bits, and instructions were built up from units 20 bits in length. As well, Chen-Ho encoding of decimal numbers compresses three decimal digits into a compact 10-bit unit. A 10-bit unit allows access to all of these data types, as well as the 60-bit floating-point format, and 10 bits is not an unreasonable size for characters. Thus, at the cost of some of the intended flexibility of the architecture, addressing could be built around only one basic unit, that of 10 bits, because that would provide access to memory operands of all fundamental types, if not of all the possible lengths envisaged.
A 15-bit unit allows somewhat simplified conversion to physical memory addresses of the addresses of most, although not all, of the items accessible with a 10-bit unit. In addition, a 15-bit character width could be a convenient alternative to the full 16-bit character width required for the whole Unicode Basic Multilingual Plane under some circumstances.
An 8-bit unit is needed if characters of conventional 8-bit and 16-bit size are to be handled on the system.
The diagram on the left shows how addresses could be converted, starting from whichever basic unit is used, to produce either an address in terms of the 720-bit fundamental width of the architecture, or in terms of the likely 120-bit physical data bus. The stacked rectangles depict addresses; as breaking down memory from, for example, a 40-bit word into 20-bit and 10-bit units successively extends addresses by one additional bit at the least significant end at each step, the rectangles representing addresses in a power-of-two relationship are shown in a stack that gradually extends to the right.
Hardwired divisions by 3, 11 in binary, and by 15, 1111 in binary, are the only ones employed, in the hopes that circuitry for divisions by divisors of this special form can be made reasonably efficient. Note that by employing a non-uniform form for the displacements, this circuitry, except for the use of one multiply by three stage to convert from the addresses of 720-bit units to physical addresses for 120-bit memory words, need only be employed when addresses are indexed.
In this scheme, several data types would have multiple alternate sets of opcodes for the instructions that affect them, in order to indicate which basic memory unit would apply if the instruction was indexed. Will an 8-bit opcode be sufficient given the additional opcodes this will require?
The basic types for which a full set of 16 operations would be provided would only be the binary integer and floating-point types. With an 8-bit opcode, four bits are used to indicate the operand type, and four bits are used to indicate the operation. Having one type appear as multiple types, depending on the indexing option chosen, increases the length of the list of these types to the following:
Binary Integers 30-bit integer with 15-bit unit 30-bit integer with 10-bit unit 60-bit integer with 15-bit unit 60-bit integer with 10-bit unit Floating-point numbers 36-bit floating-point; 12-bit unit only 40-bit floating-point; 10-bit unit only 48-bit floating-point; 12-bit unit only 60-bit floating-point with 12-bit unit 60-bit floating-point with 10-bit unit 60-bit floating-point with 15-bit unit 120-bit floating-point with 12-bit unit 120-bit floating-point with 10-bit unit 120-bit floating-point with 15-bit unit
Thus, the number of types thus created are less than sixteen. The nine-bit unit is not used, and even though 8-bit characters are used, it is not considered worthwhile to use the 8-bit unit for addressing of 48-bit floating-point quantities.
The memory-to-memory instruction format shown above for instructions starting with the bits 10 is likely to be used only with character and decimal data, so all 256 possible operand values can be used for the various types of these operands without conflict. Not shown above is the format of vector instructions, which it is assumed will begin with 11.
As for the character sets employed:
6-bit characters would specify the characters from U+0020 to U+0060, thus representing the 6-bit upper-case only subset of ASCII in order; 000000 would be a space, 111111 would be a question mark.
8-bit characters would be those of ISO 8859-1, the first half being the characters of U.S. ASCII, the second half including a few special characters, as well as the accented characters of the most well-known European languages.
9-bit characters could be those from U+0000 to U+01FF, thus including both those of ISO 8859-1 and the Latin Extended-A characters and the first 128 of the Latin Extended-B characters.
An alternate possibility is ISO 8859-1, U+0000 to U+00FF, and U+0300 to U+03FF for the second half, to provide Greek characters,
The set of 10-bit characters could begin with U+0000 to U+00FF, ISO 8859-1, and continue with U+2000 to U+208F, U+20A0 to U+20BF, U+2100 to U+213F, and U+2150 to U+215F, to fill the next 256 characters with most of the defined portions of General Punctuation, Superscripts and Subscripts, Currency Symbols, and Letterlike Symbols, as well as the fractions from Number Forms. And then it would continue with U+2200 to U+237F to obtain Mathematical Operators and most of Miscellaneous Technical, leaving 32 characters unused, and finishing with U+2190 to U+21FF for Arrows.
The set of 12-bit characters could consist of U+0000 to U+01FF, and then U+0300 to U+06FF for Greek, Cyrillic, Armenian and Hebrew, leaving enough space to also include Georgian, in U+10A0 to U+10FF, in the first half, with the second half consisting of all the characters from U+2000 to U+27FF.
One could use only 2,048 characters by starting with U+0000 to U+01FF, followed by U+0300 to U+03FF, so that the first 384 characters would be those of ISO 8859-1, Latin Extended A, most of Latin Extended B, and Greek (as well as combining diacritics), followed by U+2000 to U+23DF, and then U+2440 to U+245F for OCR symbols, and then finally U+02600 to U+026FF, for a more selective combination of most of the characters noted above, leaving another 2,048 positions available for other uses.
It was noted that a 40-bit floating-point type, while unnecessary from the point of view of offering a suitable range of floating-point precisions, was added to the architecture in order to allow the efficient handling of a floating-point type shorter than the 60-bit double-precision floating-point type in cases where large, sparse arrays which could not be usefully cached were involved in computations.
One is to draw inspiration from the IBM System/360 Model 44. It offered the special feature of speeding up floating-point computations by reducing the precision of double-precision floating-point numbers; while they would still be aligned on 64-bit boundaries in memory, they could be changed to 40, 48, or 56 bits in length instead of 64 bits.
For this architecture, just two types would be added: 36-bit float in 40-bit cell, and 48-bit float in 60-bit cell.
A second measure, which under some ideal circumstances would allow wasting memory to be avoided, would involve the 120-bit memory word into two parts. These two parts would be treated as belonging to separate blocks of memory which would be assigned to completely independent portions of the virtual memory address space, and which could even be assigned to separate processes. This would not be hidden from the CPU by an external memory controller, because the fact that the physical address is the address of a 72-bit item or a 48-bit item would allow steps in address arithmetic to be omitted in the CPU, but it would be at the level of the memory-mapping system, and thus not directly visible to programs (although programs would request allocations of memory of this form through operating system calls).
Since 72 plus 48 equals 120, the first 72 bits of each memory word would belong to a memory block from which fetching individual 36-bit floats would never require more than one 120-bit memory word to be fetched, and the last 48 bits of each memory word would belong to a memory block from which fetching individual 48-bit floats would never require more than 120-bit memory word to be fetched. This is less efficient when data is fetched from consecutive locations, as now either ten or fifteen fetches are required, instead of six, to fill an internal 720-bit block, and so it would only be used for large sparse arrays which should not be cached.
The diagram on the right illustrates the additions that would need to be made to addressing logic to enable it to produce external physical 72-bit or 48-bit addresses, as would be required by this mode.
Note that the lengths of the mantissas, including the hidden first bit (where applicable), for the various floating point formats are:
Format Mantissa 36 bits 27 bits 40 bits 30 bits 48 bits 38 bits 60 bits 49 bits 120 bits 104 bits
The number of bits that can be handled by a Sklansky adder, as a function of the number of stages in that adder, is the sequence of powers of two. Thus, 36-bit and 40-bit floats would use one adder, 60-bit and 48-bit floats would use another, and 120-bit floats would use yet another one.
The number of inputs that a Wallace Tree multiplier can handle, as a function of the number of stages, is the sequence 3, 4, 6, 9, 13, 19, 28, 42, 63, 94, 141... as is noted on this page. Thus, multiplication of 36-bit floating point numbers would use a 7-stage Wallace Tree, that of 48-bit and 40-bit floating point numbers would use an 8-stage Wallace Tree, that of 60-bit floating point numbers would use a 9-stage Wallace Tree, and that of 120-bit floating-point numbers would use an 11-stage Wallace Tree.
One thing that had led me to seek solutions other than the one described here is that I felt that there was no circuit that could perform division by 3, 5, or 7 efficiently enough to be acceptable.
While that may still be true, further thought on the issue has enabled me to see that, at least, the problem is not quite as difficult as I had originally envisaged.
The Burroughs Scientific Processor was a computer that operated on vectors, and in order that matrix multiplication would be efficient, it had what would be called seventeen-channel RAM today. As long as the size of a matrix was relatively prime to the odd prime number 17, then, not only could seventeen successive numbers in a row of the matrix be fetched at once, but so could seventeen successive numbers in a column of the matrix be fetched at once, because their locations would all have a different value modulo 17.
The trick to dividing quickly by 17 is this:
255, which is one less than 256, is equal to 15 times 17.
So divide by 255. Then multiply by 15.
Multiplying by 17 is easy - add the integer to itself shifted left four places (multiplied by 16). Multiplying by 15 is just as easy - subtract the integer from itself shifted left four places.
The reciprocal of 255, in binary notation, is .000000010000000100000001... and, therefore, multiplying by that requires only a limited number of additions. The quickest way to do that would be, for a 32 bit address:
Two additions. Three for a 64-bit address on a modern machine.
This result would actually have to be divided by 256 as well to be the address divided by 255, since we multiplied by 1.0000000100000001... but that will turn out to be useful.
But wait! Multiplying by a reciprocal gives an approximate result. For addressing calculations, what is needed is an exact result.
So there is one more thing we need to do.
If we think of the address as a number with base-256 digits, then, multiplying by .1111... in base 256 will result in sums of those digits.
If you add all the digits of a decimal number together, you can get its exact remainder when divided by nine. So we're very close to an exact answer; we just have to do one thing differently. What is it?
Well, 100 is equal to 99 plus 1. And so 100 divided by 9 is 11 1/9.
So instead of taking 11.1111... with the ones going on forever, and cutting them off to get 11.1, an approximate result, if we treat the final digit as a fraction out of 9 instead of a decimal out of 10, our result is exact.
Thus, in the case of dividing by 255, we perform the additions and shifts as noted above, but we treat the final eight bits of the accumulator in a special way, so that we're doing mixed-radix arithmetic; most of the accumulator is binary, but the last eight bits are to be handled as containing a number modulo 255. The simplest way of doing it is to add one to the last byte whenever there is a carry out of it.
Then the last byte contains the remainder modulo 255, and the earlier part of the accumulator has the quotient.