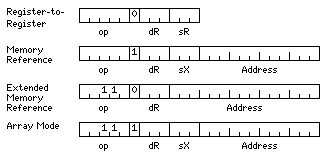
Instead of taking inspiration from the PDP-8, perhaps a computer with a 12-bit word could still have a more modern architecture:

The instructions might be:
0 0000 A Add 0 0001 S Subtract 0 0010 M Multiply 0 0011 D Divide 0 0100 L Load 0 0101 ST Store 0 0110 ML Memory Load 0 0111 MST Memory Store 0 1000 N And 0 1001 O Or 0 1010 X XOR 0 1011 ISZ Increment and Skip if Zero 0 1100 IOT Input/Output 0 1101 OPR Operate 0 1110 JMP Jump 0 1111 JSR Jump to Subroutine
With respect to a small 4 Kword memory, instructions would allow source operands for arithmetic operations to be in memory. This does not seem unreasonable, since today that is a size for an L1 cache.
But with respect to a larger memory of 32 Kwords, the architecture would be load-store.
And array accesses would be made by means of an indirect reference (using a 12-bit pointer) to a 24-bit address stored in the 4 Kword memory.
So there would be a third level of memory, 16 Mwords in size, only used for arrays, and not for simple variables.
(One thing that is lacking from the formats shown so far is some means of performing indexed accesses to the 32 Kword level of memory.)
It is envisaged that the architecture would support the following data types: 12 and 24 bit integers, 36, 48, and 60 bit floating point, and 96 bit extended precision floating point.
The twelve opcodes from 0 0000 to 0 1011 could refer to either 12 or 24 bit integers; the eight opcodes from 1 0000 to 1 0111 could refer to 24 bit integers, or to any of the three floating-point types with a hidden first bit; the eight opcodes from 1 1000 to 1 1111 could refer to 96 bit extended precision floating point or to any of the three other floating point types. An Operate instruction would be used to select which data types are to be used.
Although an IOT instruction is shown, I would presume that actual I/O would be memory-mapped as on modern microprocessors. The IOT instruction would be used for certain internal functions, such as leaving supervisor state for problem state.
The jump to subroutine instruction would store the return address in the register indicated by the destination register field. The jump instruction would be conditional; however, a three-bit condition in the destination register field, while it suffices for covering all the combinations of 'less than', 'equal', and 'greater than', does not provide for testing carry or overflow. This deficiency can be remedied by including 'skip if carry' and 'skip if overflow' instructions within the OPR opcode.
So the three logical operations, AND, OR, and XOR, as well as the looping operation, ISZ, apply only to the primary integer type in use at a given moment, which is allocated twelve opcodes; that type may be either 12 bit or 24 bit integers.
The IOT and OPR instructions may be 12 or 24 bits long, as indicated by the same bit that indicates a memory reference for most other instructions, although they do not refer to memory. This allows more opcode space as well as more uniform instruction decoding.
The JMP and JSR instructions have the same format as the ML and MST instructions; in this way, program code may reside in either the 32 Kword memory or the 16 Mword memory, but not in the 4 Kword memory.
But this design is not very well suited to an implementation with a deep pipeline; with a small number of registers, each instruction is likely to depend on the one before.
By making some small changes, though, this can be addressed:
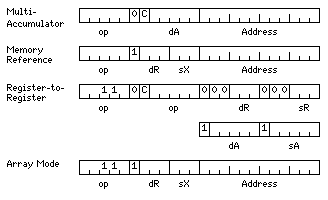
Note the C bit in some instructions, indicating whether they set the condition codes, as found on some RISC architectures.
In this alternate instruction format, only the 16 Mword external memory and the 4 Kword internal memory are accessed; the intermediate 32 Kword memory is dropped.
Extra banks of 32 registers are added. And there are register-to-register instructions which connect them with each other, or with the original group of eight registers, the only ones that can talk to the 16 Mword memory.
But because the 32 registers can perform operate instructions with the 4K word memory, instead of interleaving four calculations, each of which involve arithmetic within one subgroup of eight registers out of those 32, one could interleave up to 32 calculations using the same type of numbers by dividing the 4 Kword memory into parts used by the different calculations, and then computing with one of those 32 registers and that calculation's memory as if one were programming an older machine with a single accumulator.
So now it's possible to handle a deep pipeline without out-of-order execution without having a giant file of 128 registers. While one is still interleaving different calculations, in some ways the ISA still resembles the instruction sets of older computers.
Basically, this makes use of the fact that a 4K word memory is sufficiently small that it can be treated as if it were an extended register file, and made to operate as fast as that implies.
The rest of memory could, for example, be accessed by two 48-bit buses, each with their own address lines, to permit 60-bit floats to be accessed on 12-bit boundaries. Also, since 24-bit addresses are all indirect, opting instead for 36-bit (or 48-bit or 60-bit or even 72-bit addresses, which last woul have to be aligned on 24-bit boundaries) addresses would not be infeasible, although that means the size of an index register would need to increase to match.